Варіаційний аналіз

При вивченні тих чи інших психічних явищ не можна не помітити, що показники, які спостерігаються, відрізняються один від одного за кількісними виразами своїх ознак. Ця різниця називається варіацією.

Причини, що викликають варіацію – розходження у величині ознаки, чисельні і різноманітні. В узагальненому вигляді вони можуть бути зведені у дві групи.

1. Визначальні причини, або причини порядку закономірностей.

2. Невизначальні причини, або ті, що пов’язані з випадковими впливами на функціонування явищ, які досліджуються.

Перед математичною статистикою стоїть задача - виміряти дію й охарактеризувати обидва види причин, що впливають на величину зафіксованих ознак. Для здійснення цієї мети використовуються такі показники:

а) показники, які вимірюють вплив визначальних причин. Це середні величини: - середнє арифметичне; - медіана; - середнє геометричне; - статистична мода. Медіану і моду часто позначають: Me; Mod;

б) показники, які вимірюють вплив невизначальних причин. Це показники дисперсії , що дають узагальнену характеристику розсіювання індивідуальних випадків навколо середнього рівня або - середнє квадратичне відхилення; R – амплітуда чи розмах окремих показників; V- коефіцієнт варіації.

Середня арифметична величина

Середньою арифметичною величиною називається частка від ділення суми всіх перемінних на обсяг вибірки показників.

, тобто (13)

Нам уже відомо, що у більшості випадків дослідження проводяться вибірково. При цьому спостерігають тільки відносно малу частину всіх можливих випадків, а отримані результати і відповідні статистичні показники узагальнюються по відношенню до всієї генеральної сукупності. В такому узагальненні допускається деяка помилка, яка має назву помилкою вибірки. Величина цієї помилки, як і в альтернативному аналізі, може бути обчислена, але за допомогою дещо інших формул.

Для визначення помилки вибірки по відношенню до середньої арифметичної величини застосовується формула:

, де (14)

- величина помилки вибірки з зазначеним рівнем імовірності ( );

- коефіцієнт, що вказує на ймовірність того, що отримана величина помилки буде не більше дійсної помилки, допущеної внаслідок несуцільного спостереження;

- середнє квадратичне відхилення від угрупованого, типового показника ( );

n – число випадків у вибірці, або кількісний об’єм спостереження.

▼ Приклад на пояснення техніки обчислення . Визначити середнє число ударів пульсу за хвилину через півгодини після експериментального психоемоційного випробування (навантаження через загрозу електричного струму) у дослідженнях стресогенної толерантності спортсменів. У 25 випробовуваних виявлена середня величина 90 уд/хв., а =10 уд./хв. В межах якого інтервалу буде знаходитися середня величина числа уд./хв. пульсу після застосування загрози ввімкнення електричного струму. Ймовірність знайдених показників повинна бути .

● Рішення. Нижня границя цього інтервалу буде , а його верхня границя .

1. Визначаємо величину за формулою 14:

2. Знаходимо верхню і нижню межу дійсних відхилень пульсу від середнього показника:

= 90 – 5,16 = 84,84

= 90 + 5,16 = 95,16

Висновок. Середнє число ударів пульсу за хвилину через півгодини після закінчення експерименту знаходиться в межах між 84,84 і 95,16. Цей висновок відповідає ймовірності .

Вже ці показники можна використовувати як еталонні (нормативні) для визначення індивідуальної стресостійкості серед учасників даної групи спортсменів.

■ Зауваження.

1. При збільшенні випадків, що спостерігаються, у х раз, помилка вибірки зменшується в раз.

2. При малому числі спостережень, наприклад, при 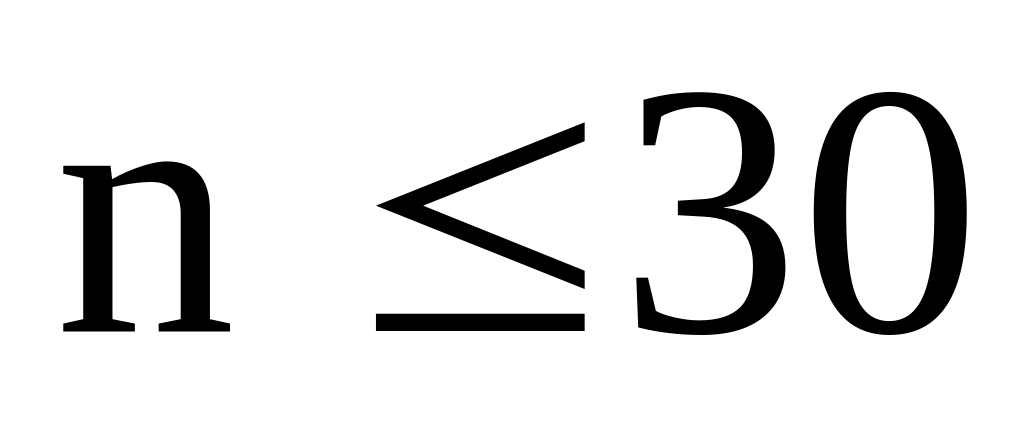, коефіцієнт t визначається по таблиці «Значення величини t при малому числі спостережень», у залежності від числа k і ймовірності .

Число k – це число ступенів свободи, що визначається у кожному випадку окремо за формулою:

k = n – 1 (15)

3. Помилка, що надходить від вибірки, характеризує собою ступінь точності (неточності) проведеного дослідження. Ступінь точності можна заздалегідь задавати (тобто планувати). Тоді треба попередньо визначати число необхідних спостережень, які забезпечать потрібну точність. Це можна зробити за допомогою перетворення формули 14 до наступного вигляду:

(16)

У науково-дослідній і практичній роботі психолога часто буває необхідно здійснювати порівняння двох середніх арифметичних. Нерідко буває потрібно на основі вибіркових спостережень зробити висновок про те, наскільки виявлені розходження між середніми арифметичними істотні, а наскільки вони є результатом впливу випадкових причин.