Альтернативний аналіз

Загальна теорія (короткі відомості прикладного значення)

Явища у прикладних психологічних дослідженнях, зазвичай, вивчаються у їх взаємозв'язках і співставленнях та розглядаються залежно від їх структури і співвідношень, у яких вони між собою знаходяться. Для цього у статистиці використовуються показники відносної долі (або показники структури) та показники співвідношення. Ті й інші показники подаються у відсотках (%), проміле (‰), продециміле (⁰/₀₀₀).

, де

m – кількість випадків, яким притаманна дана ознака;

n – загальна кількість усіх випадків.

Альтернативний статистичний аналіз має справу з випадковими, раніш не прогнозованими подіями, якостями чи ознаками. Це вказує на те, що ознака, яка досліджується у кожному конкретному випадку, може бути чи не бути, тому такі ознаки називають альтернативними. Серед альтернативних показників виділяють показники структури і показники співвідношень.

Показники структури називають екстенсивними показниками і поділяють на дві групи:

а) екстенсивно-розчленувальні – відображають виражене у відсотках співвідношення між часткою та цілим;

б) екстенсивно-вказівні – відображають виражене у відсотках співвідношення між частинами цілого.

Показники співвідношення (частоти або інстенсивності) показують частоту досліджуваних явищ. Їх також дві категорії:

а) інтенсивні – співвідношення між кількістю випадків відомої події та середовищем, у якому ця подія відбувається;

б) координаційні – співвідношення між кількістю випадків у двох явищах, між якими є непрямий зв'язок.

У роботі з альтернативними показниками не слід забувати, що

1. За вирахуваними відносними величинами стоять конкретні дані. Іноді 1% будь-якого показника за своїм абсолютним значенням дорівнює 10% того ж показника, який вирахуваний для іншого об'єкта.

2. Показники відносної долі не рекомендується підсумовувати та осереднювати.

3. Екстенсивно-вказівні величини показують відсоткове співвідношення між частинами одного й того ж цілого, тому тут можливий результат, як менший, так і більший 100%.

4. При обчисленні статистичних показників інтенсивності необхідно ретельно визначати середовище, у якому відбуваються події, що досліджуються.

5. Треба бути особливо обережним при обчисленні показників відносної долі при малочисельних вибірках.

У психологічних наукових дослідженнях використовуються два види статистичного дослідження: суцільне та вибіркове.

При вибірковому дослідженні спостереження ведеться лише за частиною випадків, які входять до об’єкту дослідження, а одержані результати узагальнюються стосовно усієї генеральної сукупності.

Вибіркові дослідження мають деякі переваги: вони дешевші, проводяться у коротші терміни, а іноді являються єдиною можливою формою дослідження. Але, у зв'язку з тим, що ці спостереження не суцільні, у них завжди наявна певна неточність, яка називається помилкою репрезентативності.

Відсоткова репрезентативність малої вибірки і допустимий інтервал точності

Наприклад, у спостереженні було виявлено певний відсоток якоїсь ознаки. Виникає питання: якщо провести інші такі ж спостереження, чи буде отриманий точно такий відсоток даної ознаки? Очевидно, ні. Одні спостереження дадуть відсоток нижчий, інші – вищий. Отже, найчастіше дати відповідь у вигляді точно визначеного відсотка не можна, а правильно буде вказати інтервал, у межах якого знаходиться відсоток, що цікавить дослідника.

Цей інтервал визначається наступним чином.

Його нижня межа дорівнює: Р - , а верхня: Р + , де

Р – одержаний у розрахунках відсоток;

- розмір неточності, яка допускається у зв'язку з несуцільним характером спостереження.

Цю величину неточності знаходять за такою формулою:

, де (1)

n – кількість випадків, за якими спостерігають;

P – винайдений відсоток;

t – так званий, довірчий коефіцієнт, що з визначеною ймовірністю вказує на величину .

При ймовірності = 0,95 (можливість помилкової оцінки складає лише 5%), а коефіцієнт t=1,96 або . При = 0,99 (помилка неточності = 1%), t = 2,58; при = 0,9973 (помилка неточності = 0,27%), t = 3 і т.д.

Значення t подане в таблиці:¹ “Значення функції ”.

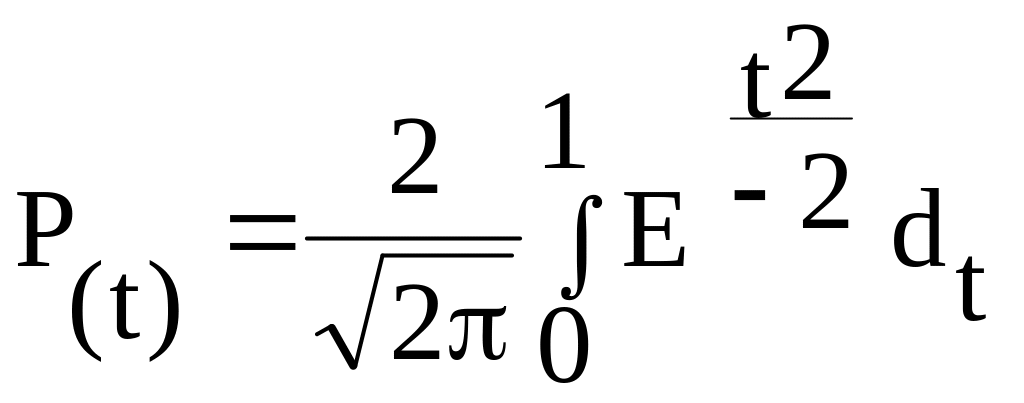У психологічних наукових і практичних дослідженнях використовуються здебільшого вказані значення коефіцієнту t.

▼ Приклад. При спостереженні за 100 довільно підібраними дітьми дошкільного віку з мовними порушеннями було встановлено, що 15 з них лівші (тобто 15%). Який дійсний відсоток лівшів серед дітей з мовними розладами?

● Рішення. При довірчому критерії ймовірності = 0,95, де коефіцієнт t =2 використовуємо формулу 1 і знаходимо інтервал ( ):

Отже інтервал, у межах якого знаходиться дійсний відсоток лівшів серед дітей з мовними розладами дорівнює кількісному показнику від 8 до 22% (15% - 7% 15% + 7%). Таким чином, з імовірністю у 95% можна бути впевненим, що дійсний відсоток лівшів серед дітей з розладами мови знаходиться у діапазоні 8 – 22 відсотків.

■ Зауваження. Якщо припустити, що спостерігалося не 100, а 400 випадково відібраних дітей з тими ж дефектами мови, і що 60 з них виявилися лівшами, то відсоток лівшів також буде 15, але інтервал, у межах якого знаходиться дійсний їх відсоток, зменшиться вдвічі. Виконаємо розрахунки.

Отже, із збільшенням числа спостережень, величина допущеної неточності зменшується.

У зв’язку з цим виникає запитання: як знаходити оптимальне число спостережень при обчисленні альтернативних статистичних показників – відносних величин?