Лекция 5. Линеаризация уравнений систем автоматического управления. Уравнения первого приближения.

Рассмотрим нелинейную систему автоматического управления, динамика которой описывается уравнениями

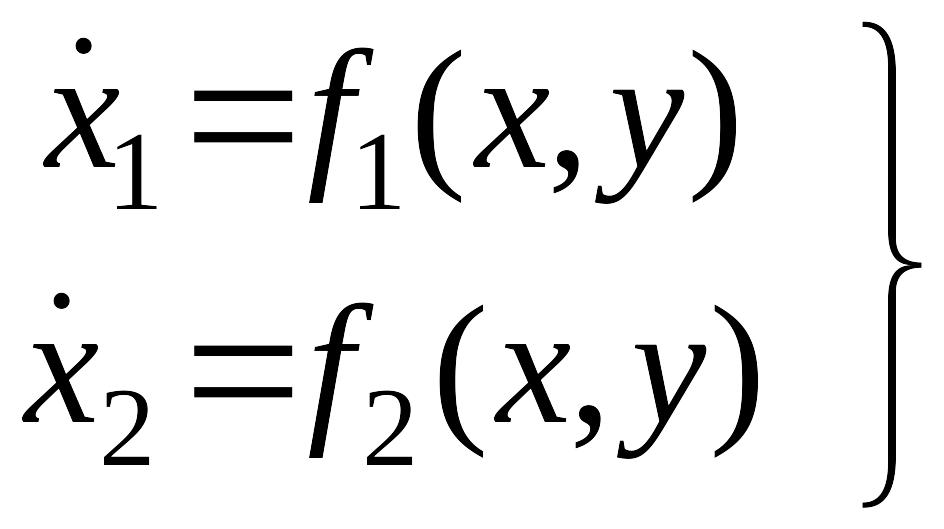, (1)

где функции и являются аналитическими во всех точках фазовой плоскости.

Определим на фазовой плоскости координаты точек, являющихся состояниями равновесия. Координаты этих точек являются решением системы нелинейных уравнений

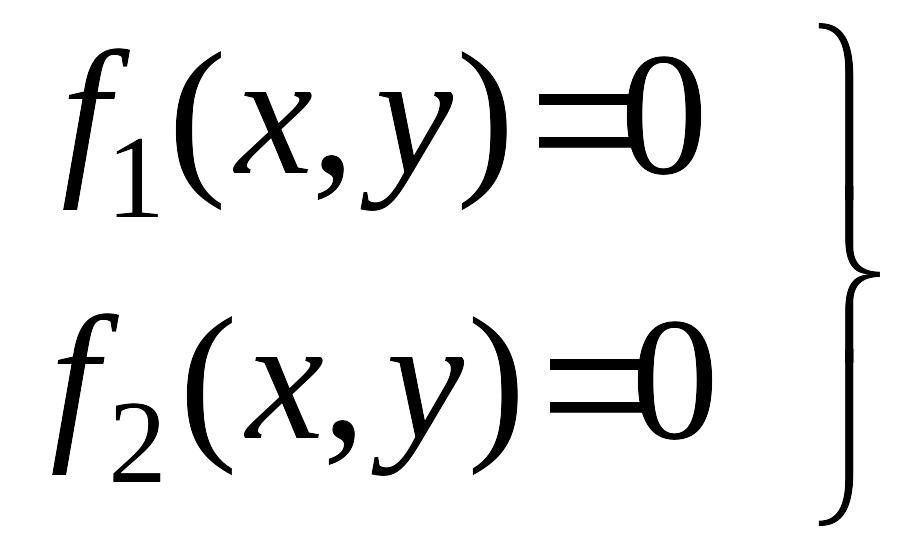. (2)

Обозначим одно из решений системы (2) через , . В общем случае система уравнений (2) может иметь несколько решений. Исследуем динамику системы (1) в некоторой окрестности этого состояния равновесия. Для этого, с помощью замены переменных

, ,

,

перенесем начало координат фазовой плоскости в особую точку с координатами (см. рисунок).

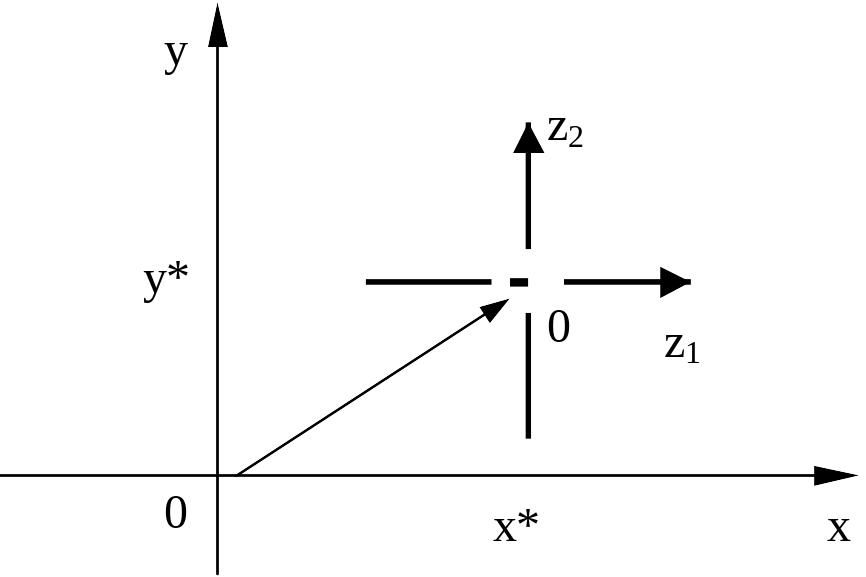
По формуле Тейлора функции и в окрестности особой точки представим в виде

,

,

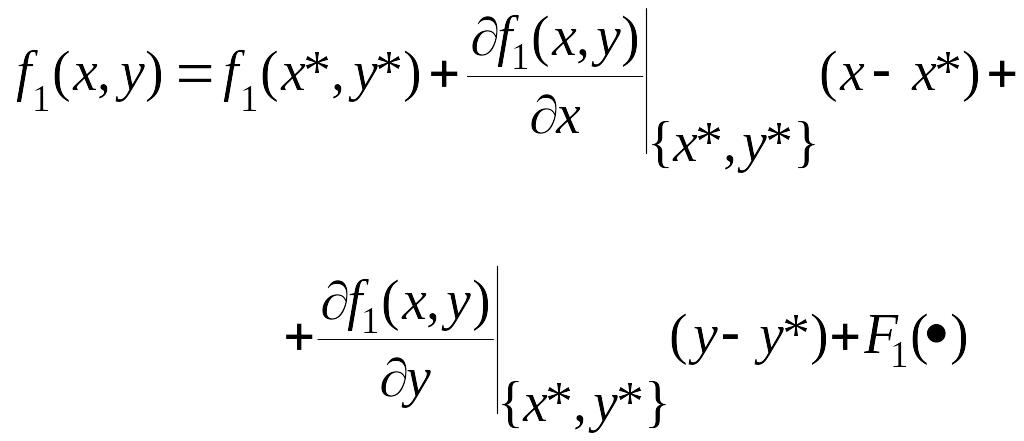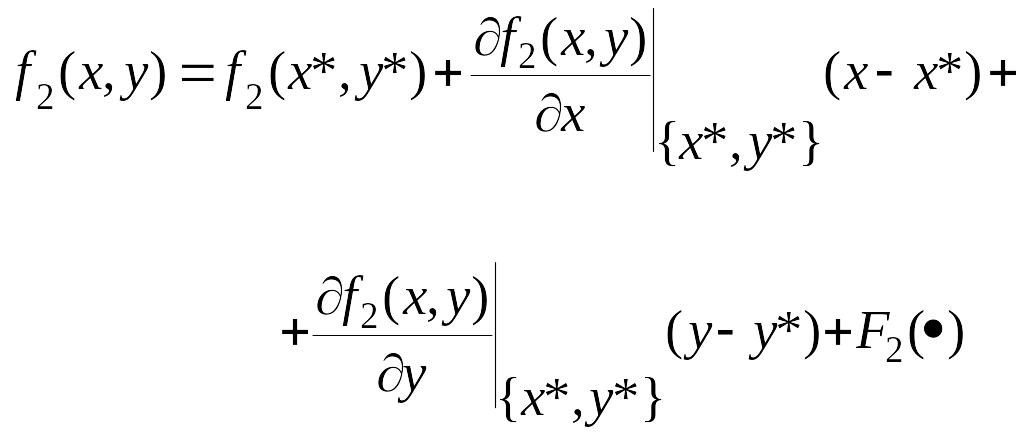где , - содержат все члены разложения функции и по формуле Тейлора, у которых степени и выше первой. Поэтому в окрестности особой точки слагаемыми и можно пренебречь. Далее поступают следующим образом.

1. Вычисляют значения частных производных функций и в точке , значения которых обозначают соответственно как , , , , то есть

, ,

, .

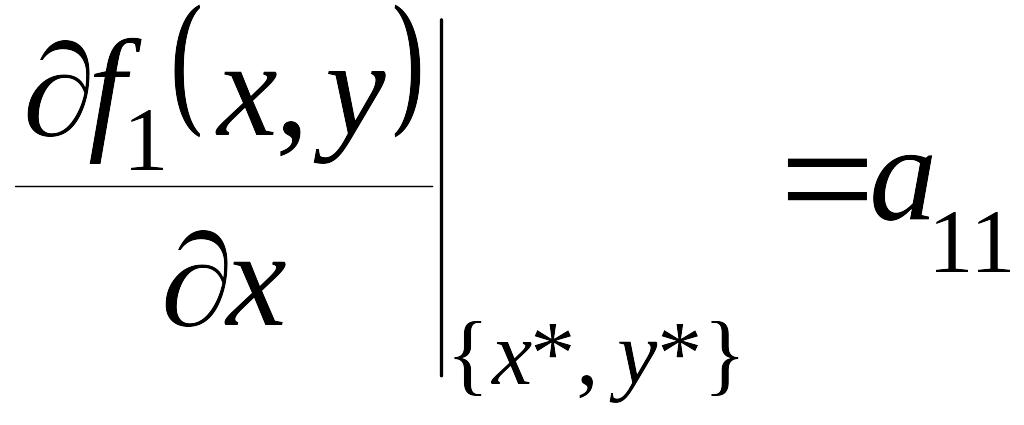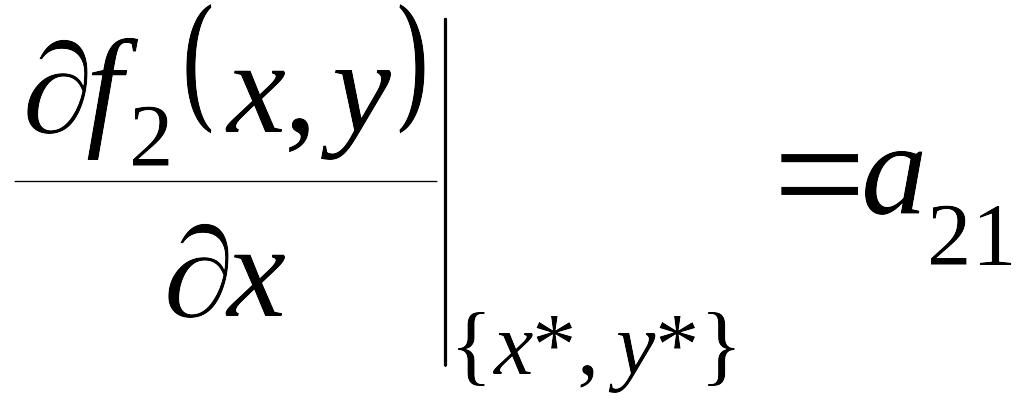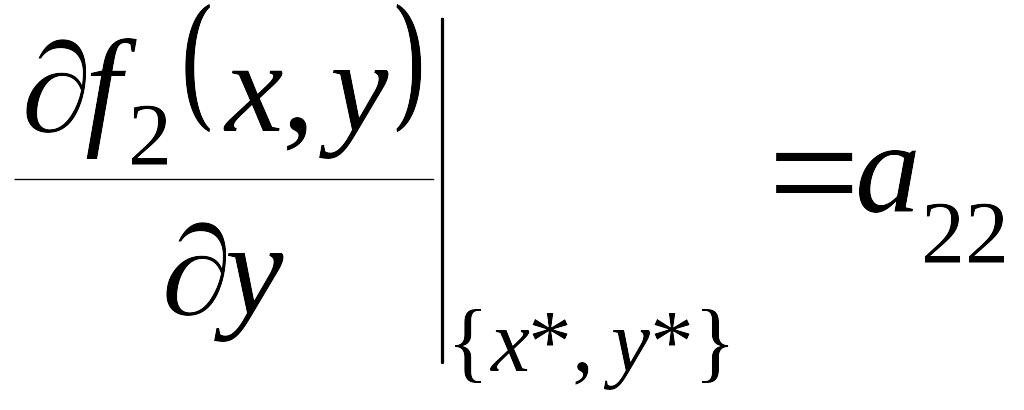Тогда

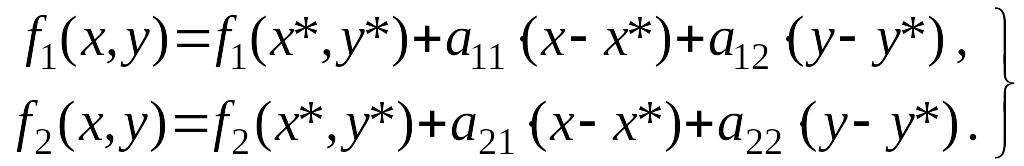(3)

2. Так как и , то

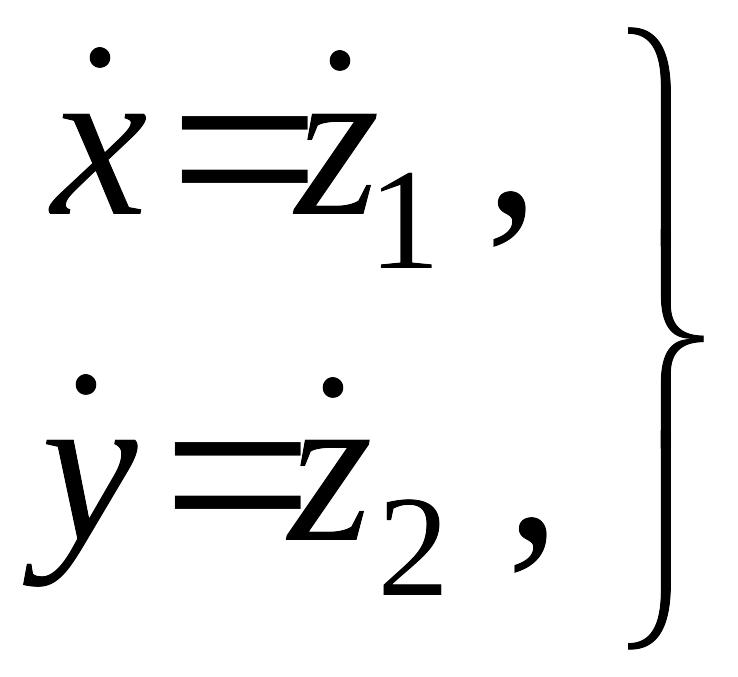(4)

, . (5)

3. Осуществляют подстановку равенств (3) и (4), (5) в уравнения (1):

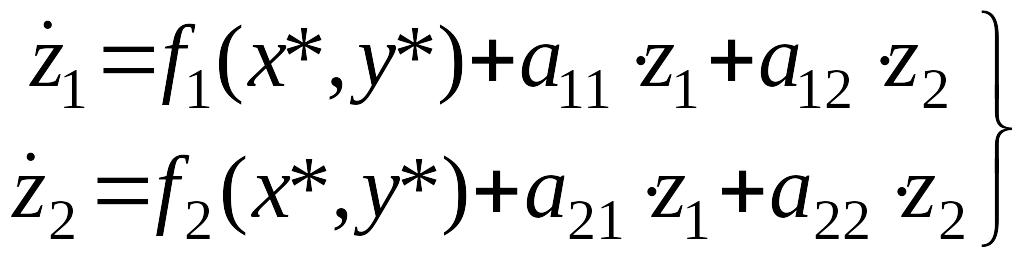. (6)

Так как в особой точке справедливо и , то окончательно получаем

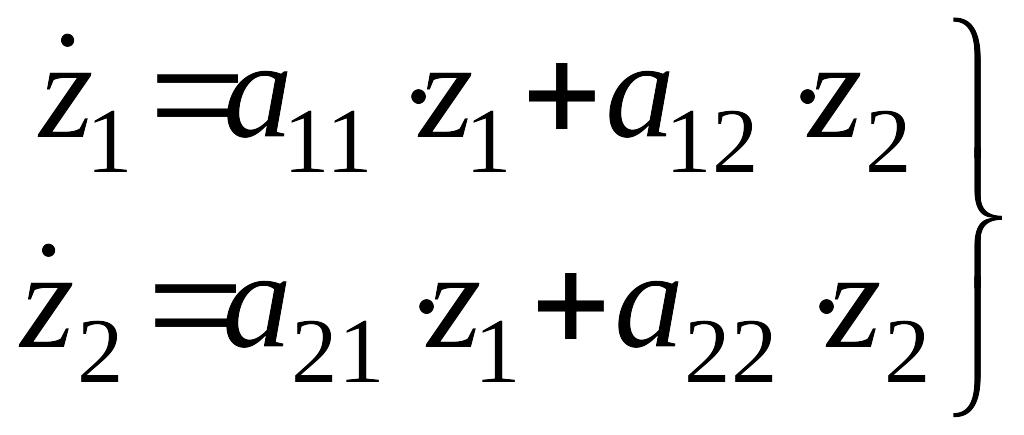. (7)

Система уравнений (7) является линейной системой дифференциальных уравнений с постоянными коэффициентами. Система уравнений (7) описывает динамику системы (1) в некоторой окрестности особой точки , в окрестности состояния равновесия системы.

Система уравнений (7) называется системой уравнений первого приближения. Динамика системы уравнения в окрестности особой точки с достаточной степенью точности описывается системой линейных уравнений (7) – уравнениями первого приближения.

Фазовые траектории нелинейных систем автоматического управления.

В случае линейных систем автоматического управления характер (тип) особой точки определяет движение системы при любых отклонениях от состояния равновесия. Для нелинейных систем характер особой точки определяет поведение фазовых траекторий лишь в некоторой малой окрестности особой точки. При рассмотрении поведения фазовых траекторий нелинейных систем на всей фазовой плоскости весьма важную роль играют особые траектории.

Различают три основных типа особых траекторий:

1. Особые точки (состояние равновесия). Типы особых точек рассмотрены выше.

2. Изолированные замкнутые траектории. Изолированность замкнутой траектории означает, что в достаточно малой ее окрестности нет других замкнутых траекторий. Изолированные замкнутые траектории называются предельным циклами. Предельным циклом на фазовой плоскости соответствуют периодические движения системы.

Предельный цикл называется устойчивым, если существует такая  –окрестность этого цикла, что все фазовые траектории, начинающиеся в  –окрестности, асимптотически при приближаются к предельному циклу (см. рисунок).

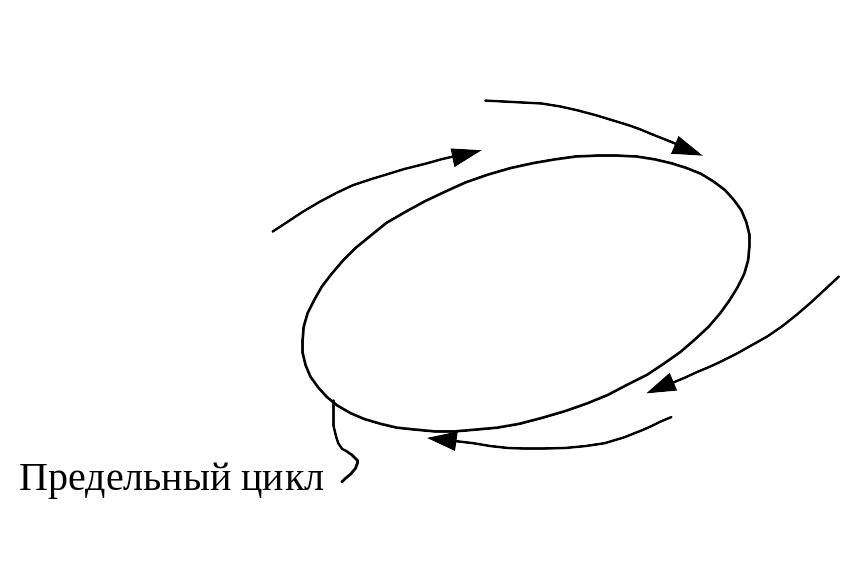
Устойчивым предельным циклам в системе автоматического управления соответствуют автоколебания. Характерная черта автоколебаний – локальная независимость их параметров от начальных условий.

Если в любой, сколь угодно малой окрестности предельного цикла существует хотя бы одна фазовая траектория, не приближающаяся к предельному циклу при , то предельный цикл называется неустойчивым (см рисунок).

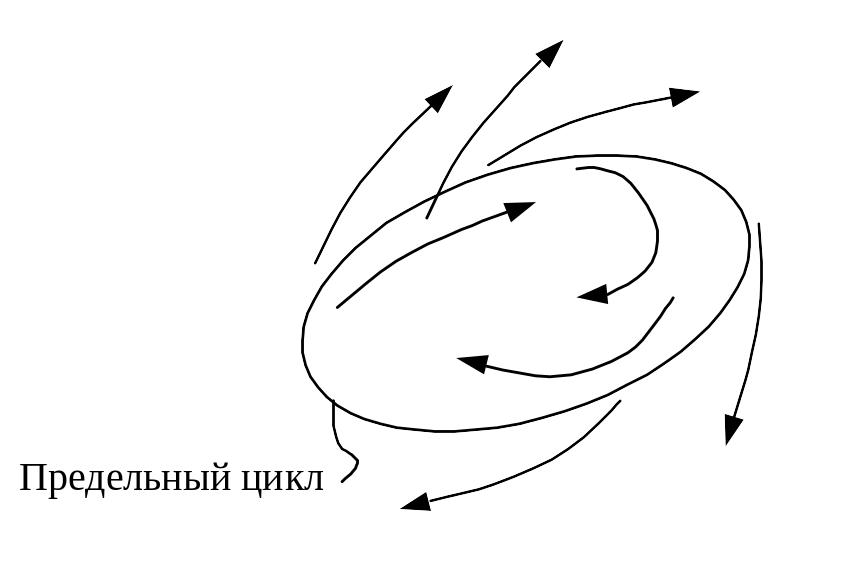
3. Сепаратрисы. Сепаратрисы разделяют фазовую плоскость на области с фазовыми траекториями различных типов. В окрестности особой точки типа «седло» сепаратрисы – являются асимптотами. Точки равновесия, предельные циклы и сепаратрисы являются особыми траекториями. Таких траекторий обычно имеется конечное число на фазовой плоскости. Определив эти особые траектории, мы тем самым находим все качественные особенности фазовых траекторий на плоскости, все виды и особенности процессов в нелинейных системах. Особые траектории разбивают всю фазовую плоскость на ряд областей; характер движения в каждой из этих плоскостей часто бывает нетрудно определить, зная характер устойчивости точек равновесия и предельных циклов. Так получается полная качественная характеристика всех возможных типов движений системы.

Особые траектории разбивают фазовую плоскость на ряд областей. Характер движения в каждой из этих областей нетрудно определить, если известен характер особых точек и определена устойчивость предельных циклов. Таким образом, можно получить качественную картину всевозможных движений динамических систем.