Случай 1. Корни характеристического уравнения – чисто мнимые (Центр).

Рассмотрим дифференциальное уравнение

, (1)

характеристическое уравнение которого, будет иметь вид

. (2)

Корни характеристического уравнения

. (3)

Пусть начальные условия для уравнения (1) заданы

, .

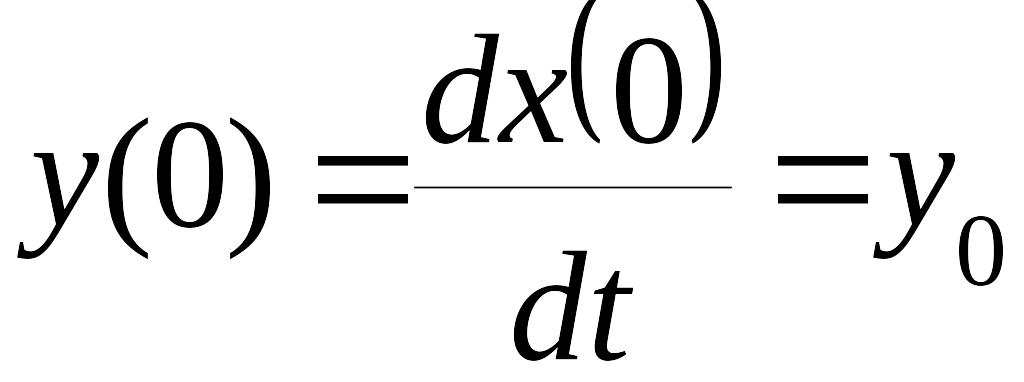Получим уравнение фазовых траекторий. На основании (3) решение дифференциального уравнения (1) имеет вид

, (4)

где и – постоянные интегрирования, которые определяются заданными начальными условиями. Вычислим постоянные интегрирования и . Для этого вычислим предварительно производную по времени

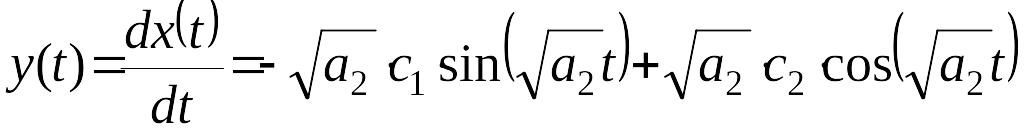. (5)

Теперь используем заданные начальные условия

.

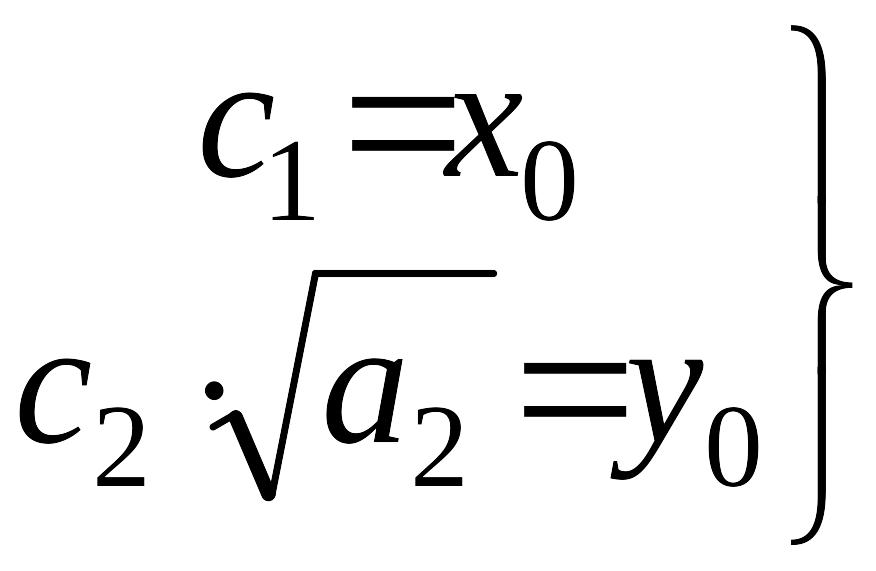Таким образом

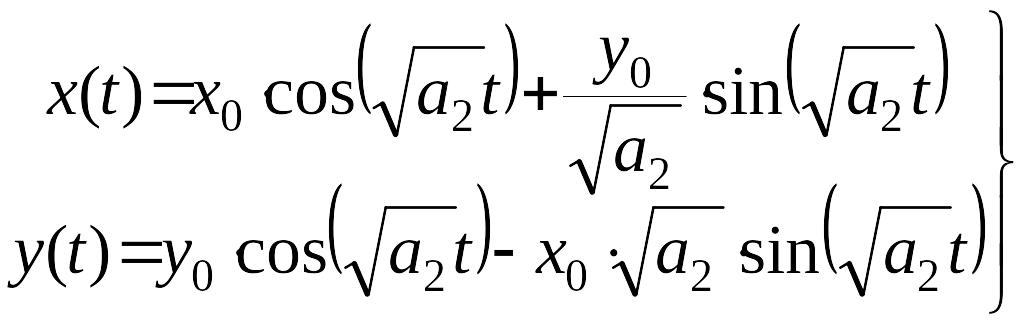. (6)

Для того, чтобы получить уравнение фазовых траекторий, нужно из уравнений (6) исключить время . Из уравнений (6) последовательно получаем

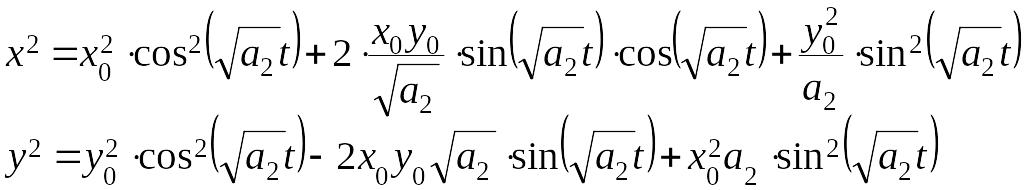
Умножим первое уравнение на и сложим со вторым

,

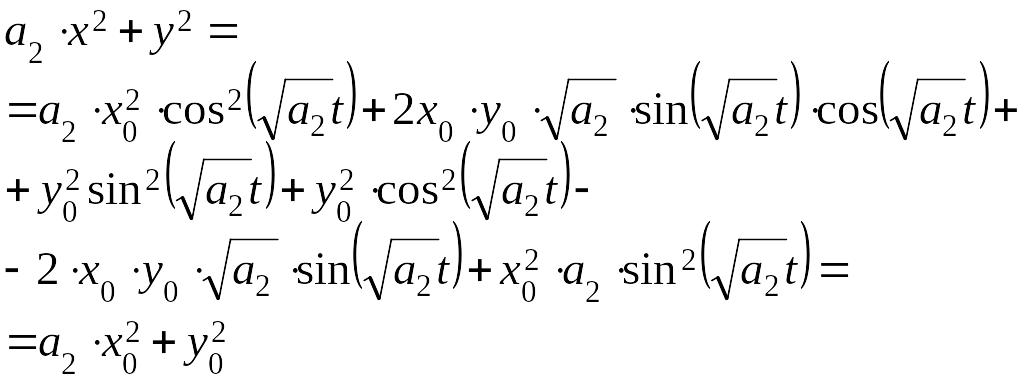откуда получаем

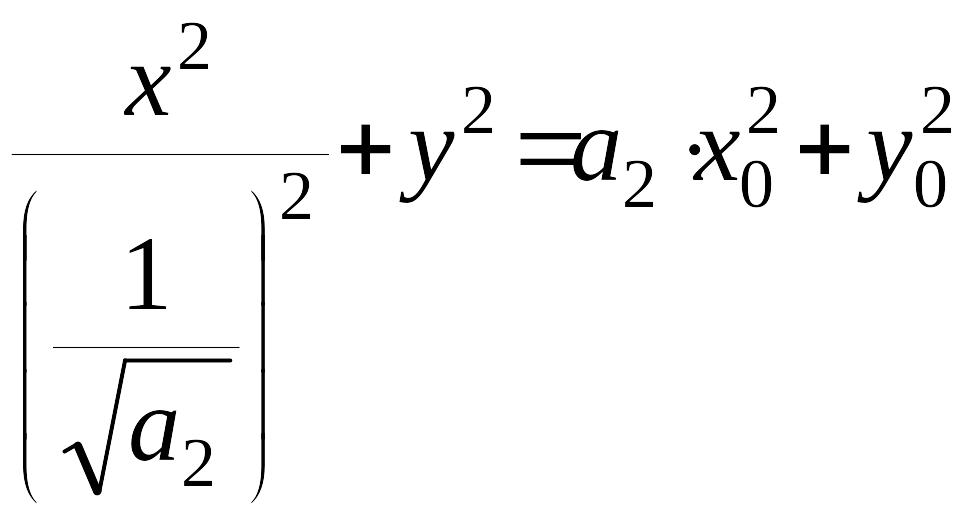(7)

Из уравнения (7) находим

при ,

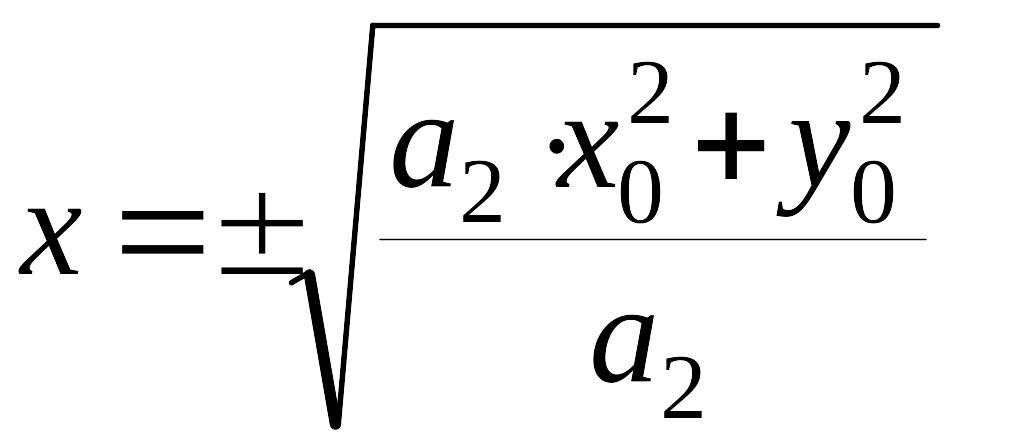при .

Тогда уравнение (7) преобразуется к виду

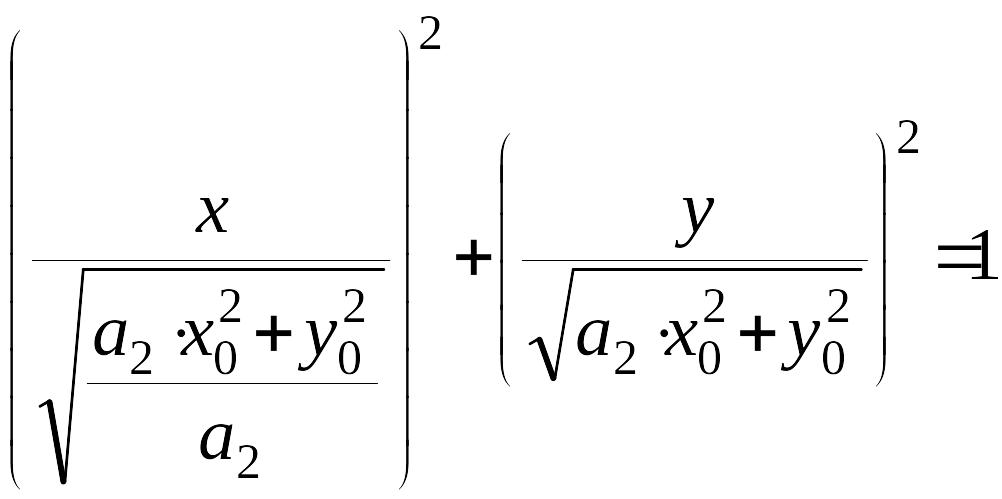
Таким образом, фазовые траектории – это эллипсы с центром в начале координат и полуосям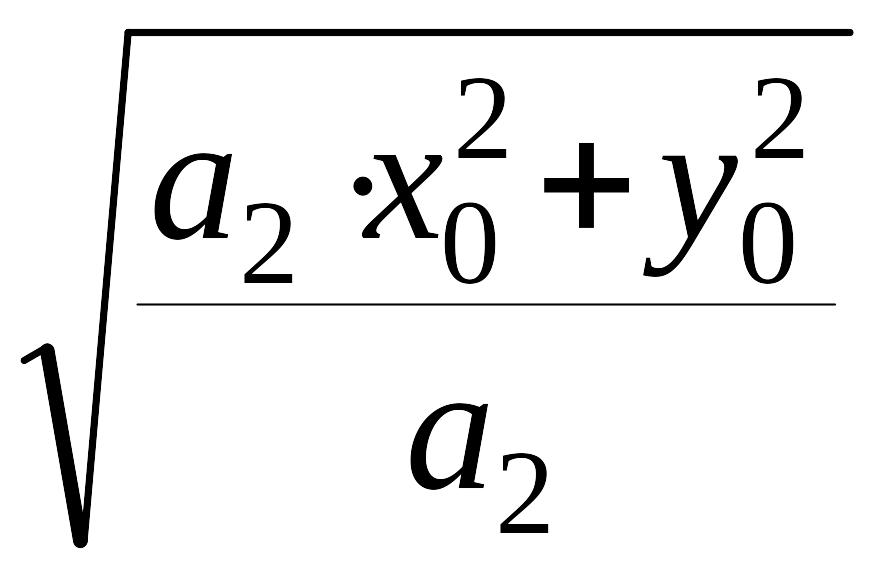и

и .

Укажем другой способ получения уравнений фазовых траекторий. Из уравнения (1) получим систему уравнений

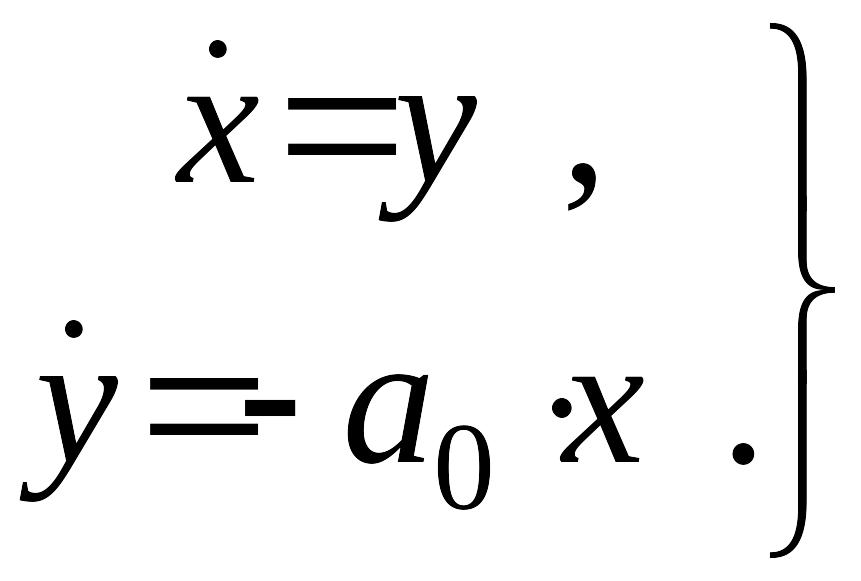. (8)

Поделим уравнения системы (8) (второе на первое)

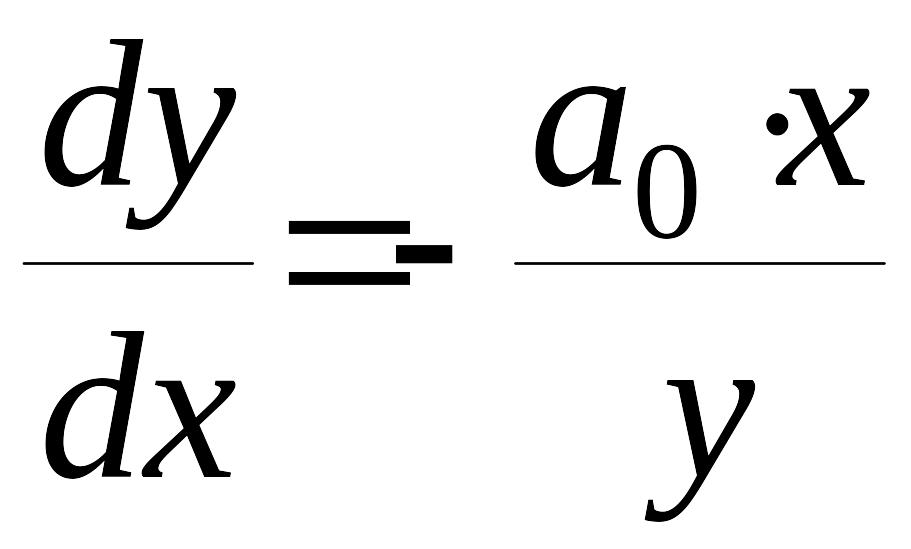, (9)

Полученное уравнение – это линейное дифференциальное уравнение с разделяющимися переменными. Решим это уравнение

, (10)

,

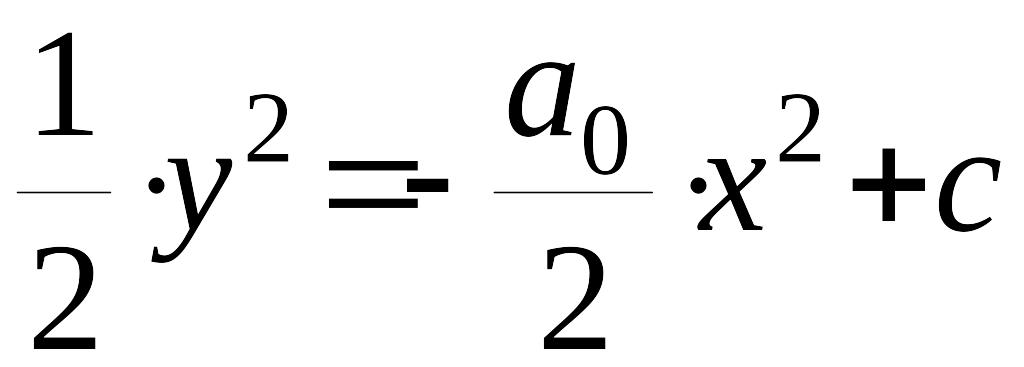, (11)

где – постоянная интегрирования. Если теперь положить, что постоянная в (11) выбирается из заданных начальных условий , согласно равенству

,

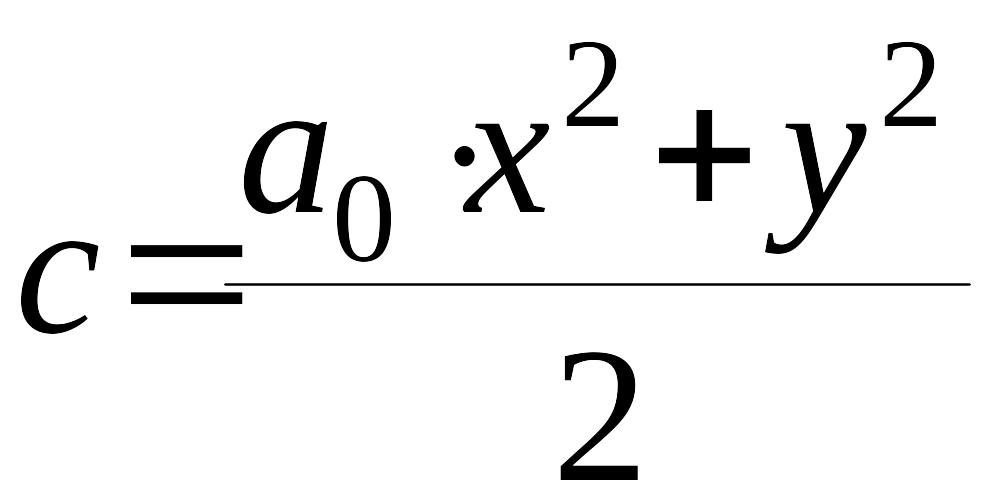то равенства (7) и (11) совпадают.

Вывод. Если корни характеристического уравнения соответствующего дифференциального уравнения являются чисто мнимыми числами , то фазовые траектории представляют собой концентрические эллипсы с центром в начале координат, а особая точка называется центром.

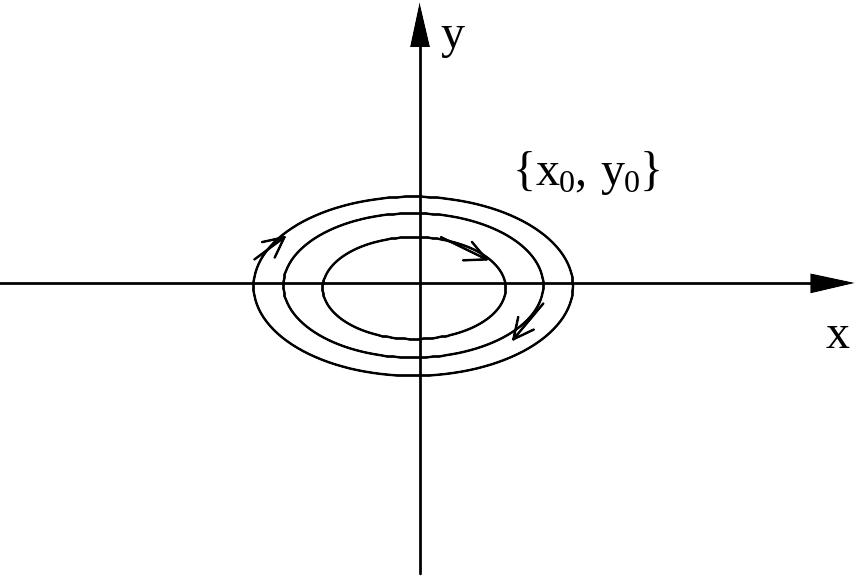
Случай 2. Корни характеристического уравнения – комплексно-сопряженные (фокус)

Рассмотрим дифференциальное уравнение

, (1)

начальные условия , считаем заданными. Выпишем характеристическое уравнение, соответствующее дифференциальному уравнению (1)

, (2)

его решение имеет вид

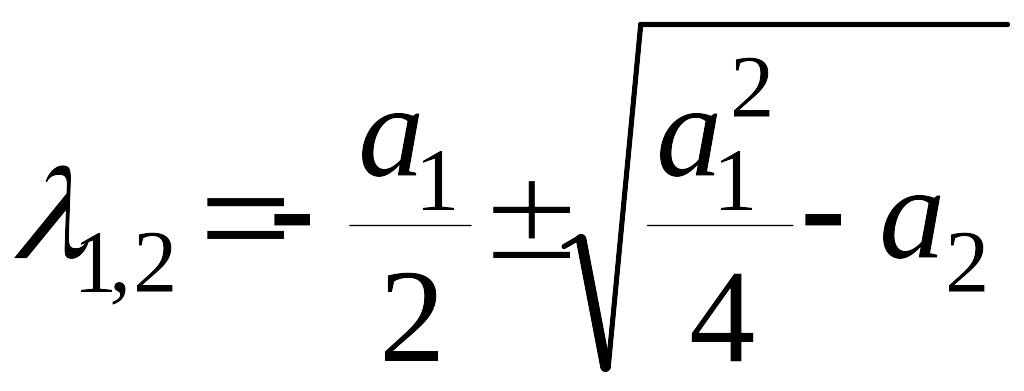, (3)

Пусть теперь параметры уравнения (2) таковы, что выполняются неравенства

, . (4)

Введем обозначения:

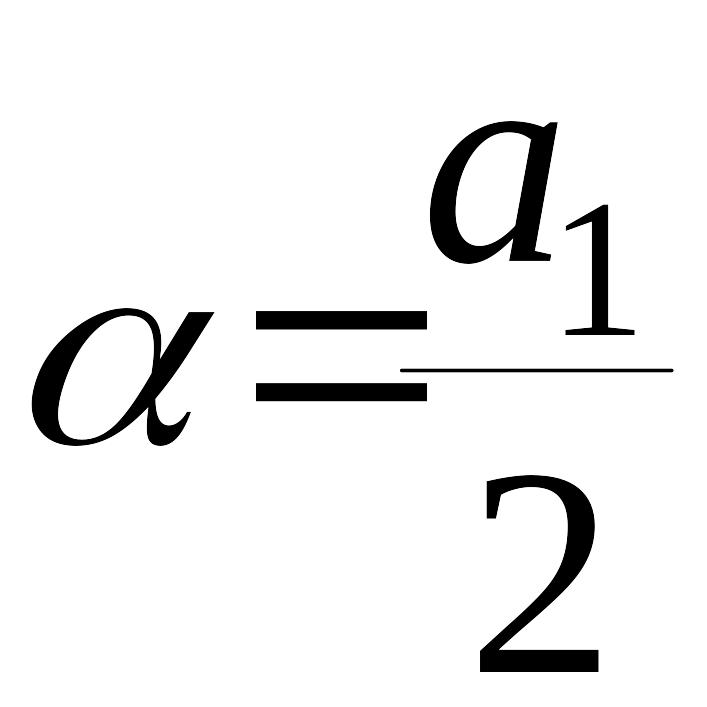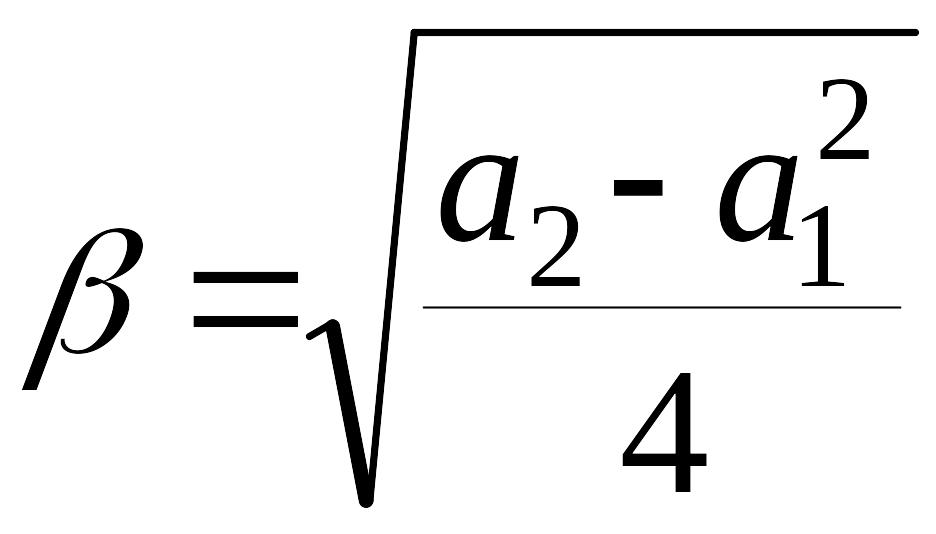, , (5)

Тогда с учетом выполнения неравенств (4) и обозначений (5), корни уравнения (2) будут комплексно-сопряженными и запишутся в виде

, , (6)

Введем в рассмотрение фазовые переменные (переменные состояния) исследуемой системы

, .

Решение уравнения (1) будет

, (7)

где и – определяются начальными условиями. Из уравнения (7) получим

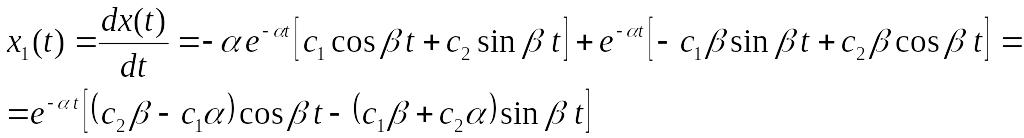
(8)

Из уравнений (7) и (8) при имеем

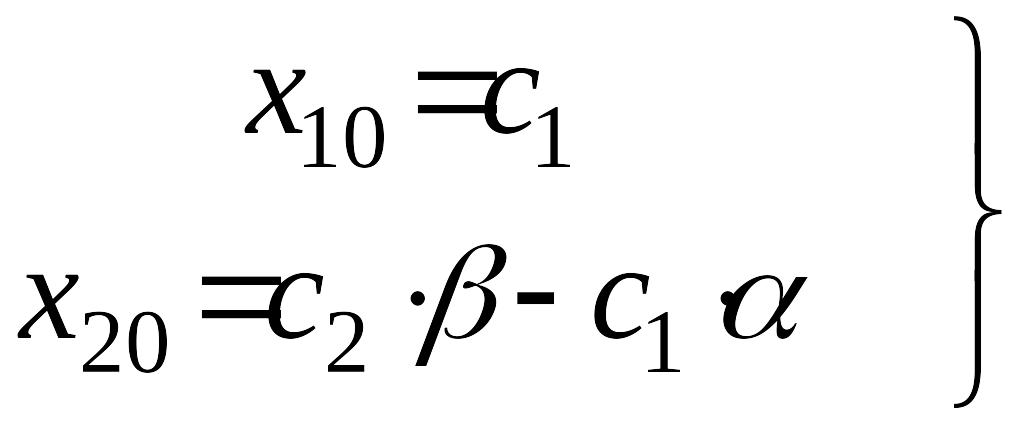, (9)

откуда получаем:

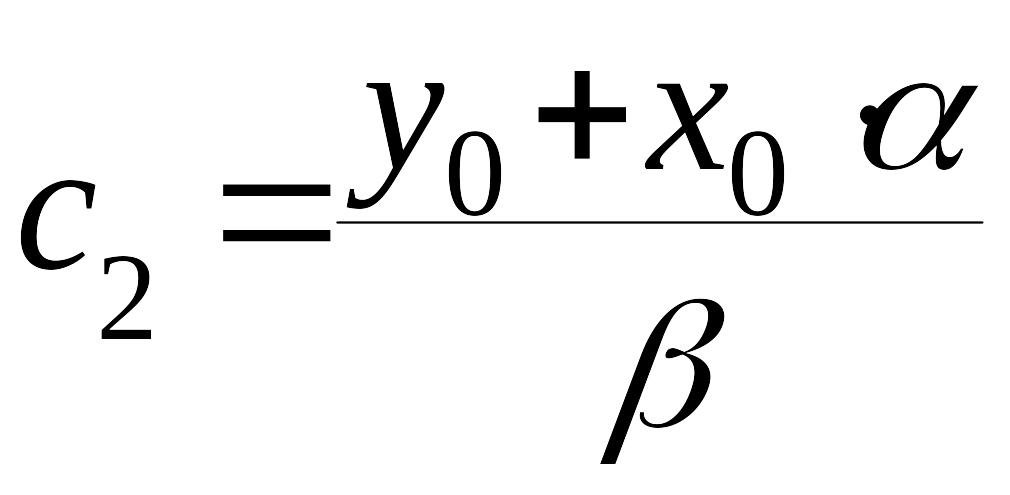, . (10)

Таким образом, уравнения (7) и (8) принимают вид

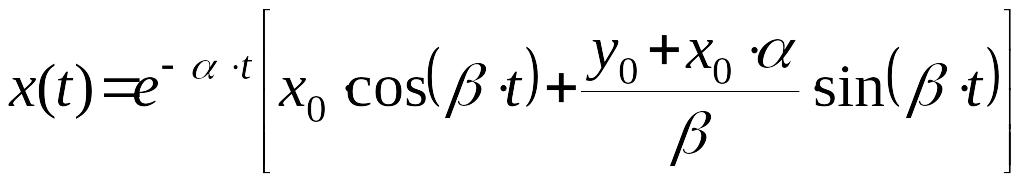, (11)

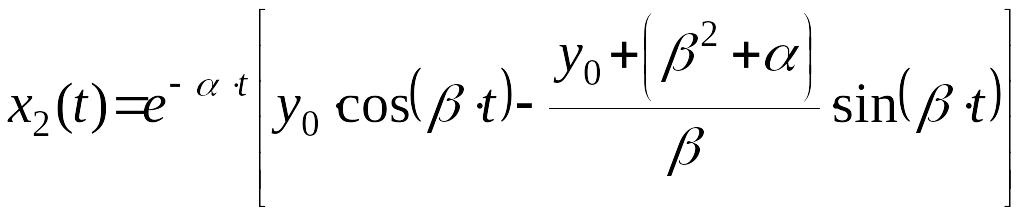. (12)

Уравнения (11) и (12) – это уравнения фазовых траекторий в параметрическом виде, параметр – время. Пусть теперь . Тогда

, .

Это означает, что изображающая точка по спиральной траектории приближается к началу координат фазовой плоскости (см. рисунок).

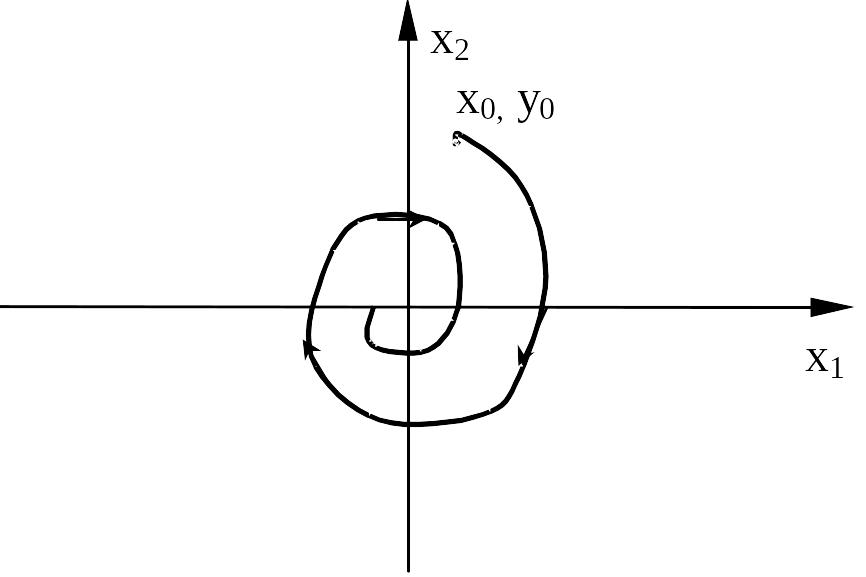
При этом процесс на выходе системы имеет вид, показанный на рисунке

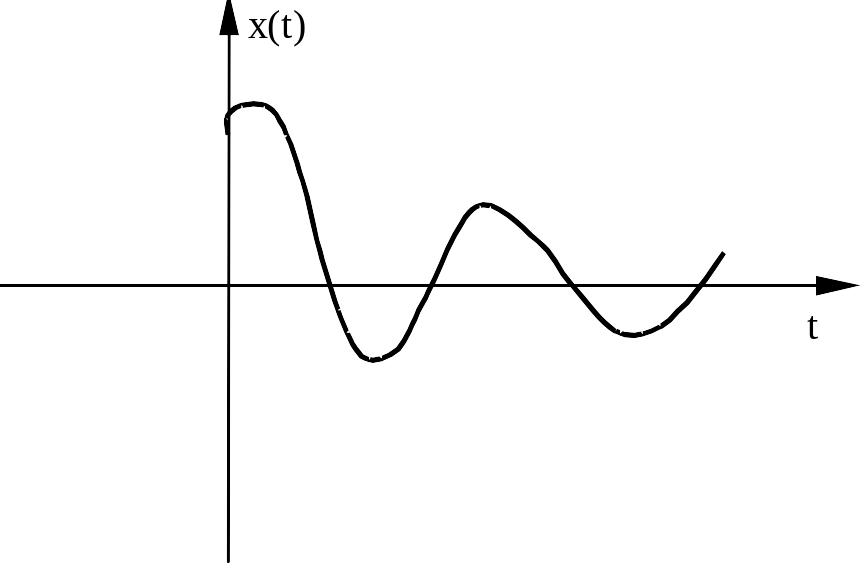
Если теперь . Тогда

, .

Это означает, что изображающая точка движется по спиральной траектории, удаляясь от начала координат фазовой плоскости (см. рисунок).

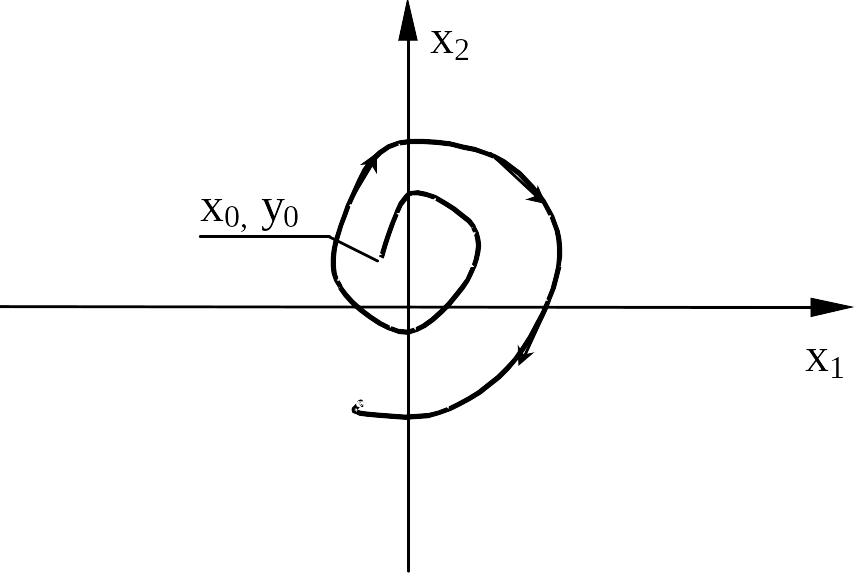
При этом процесс на выходе системы имеет вид, показанный на рисунке

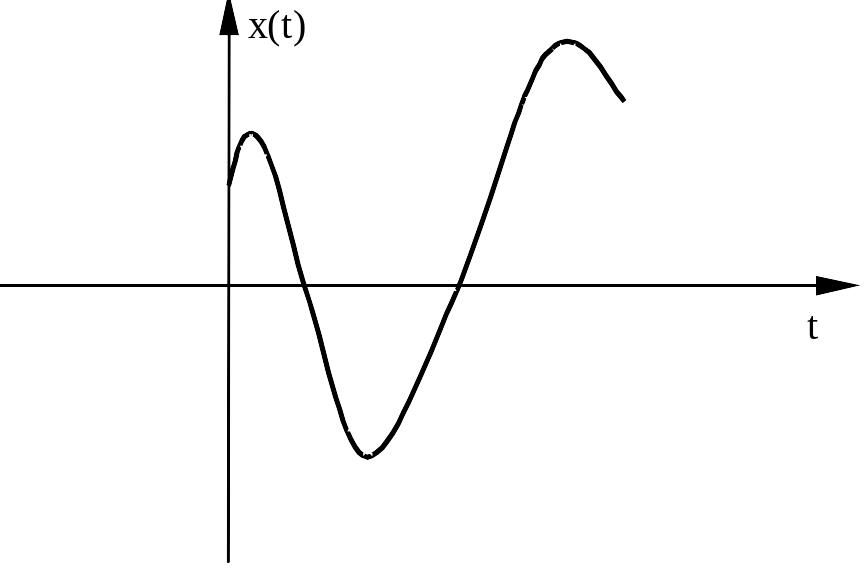
Направление движения изображающей точки определено согласно приведенному выше правилу для системы уравнений:

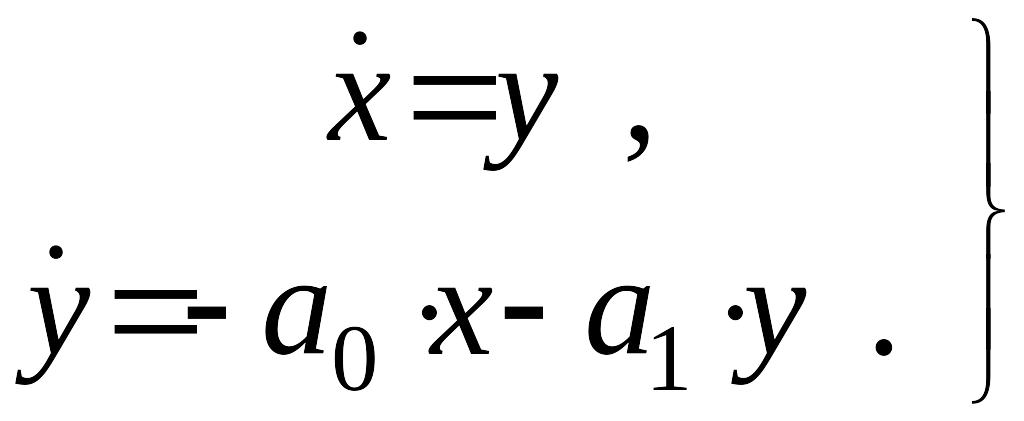
Вывод. Если корни характеристического уравнения соответствующего линейного дифференциального уравнения являются комплексно-сопряженными , то фазовые траектории представляют собой спирали с центром в начале координат, а особая точка – называется фокусом. При этом, если , то фокус – устойчивый – изображающая точка стремится к началу координат, точке равновесия; если , то фокус неустойчивый, изображающая точка удаляется от начала координат, система неустойчива.

Случай 3. Корни характеристического уравнения действительные, различные и одного знака (узел).

Рассмотрим систему автоматического управления, динамика которой описывается системой дифференциальных уравнений

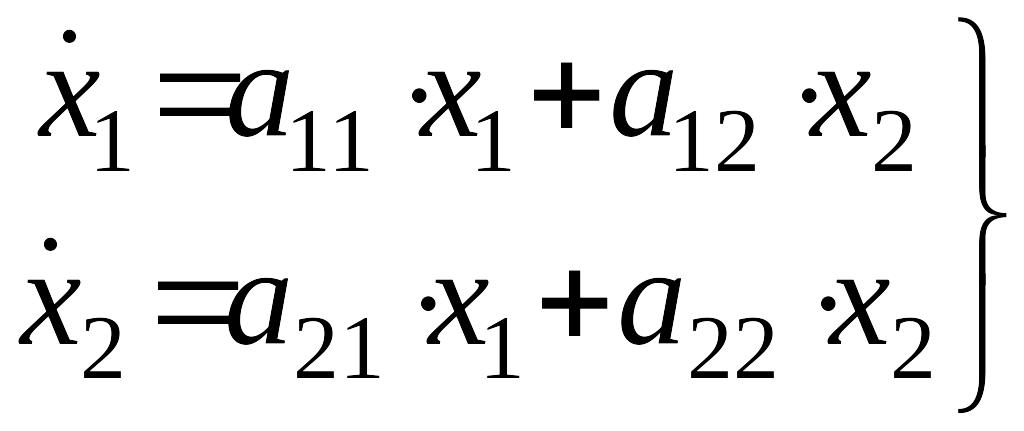. (1)

Для системы уравнений (1) матрица динамики системы управления имеет вид

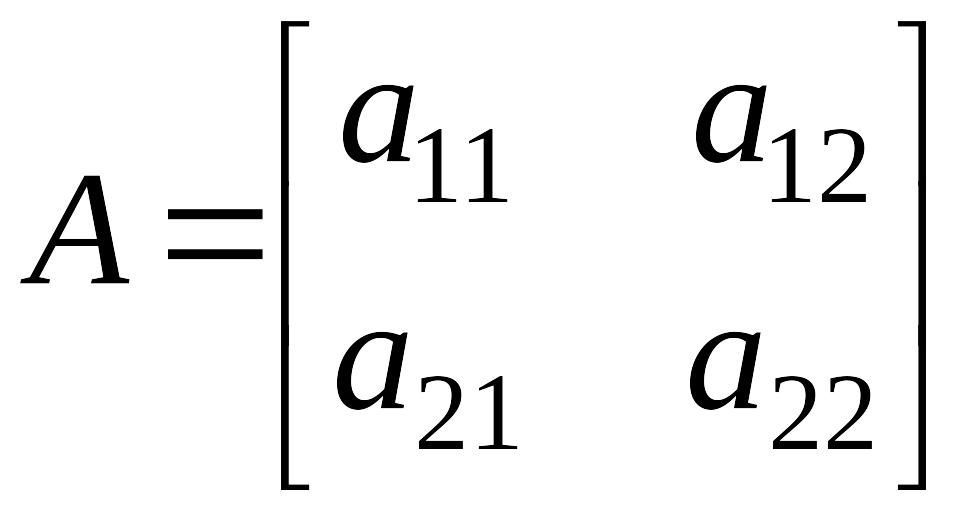, (2)

а характеристическое уравнение будет

,

,

.

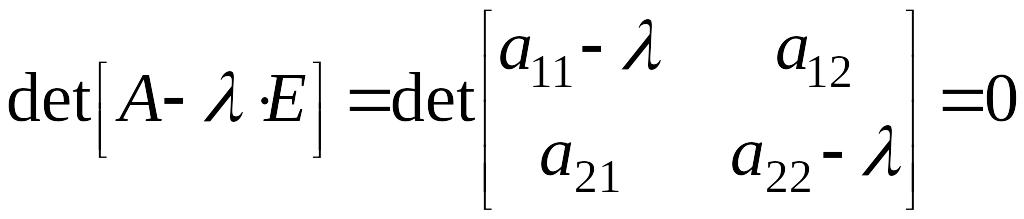Рассмотрим простейший частный случай: в уравнениях (1) .Тогда уравнение (1) принимает вид

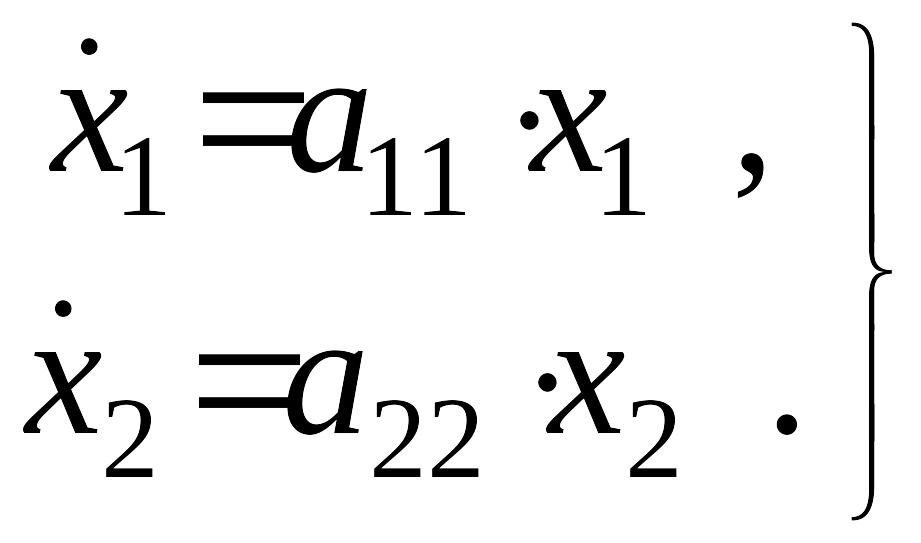. (4)

Матрица динамики системы (2):

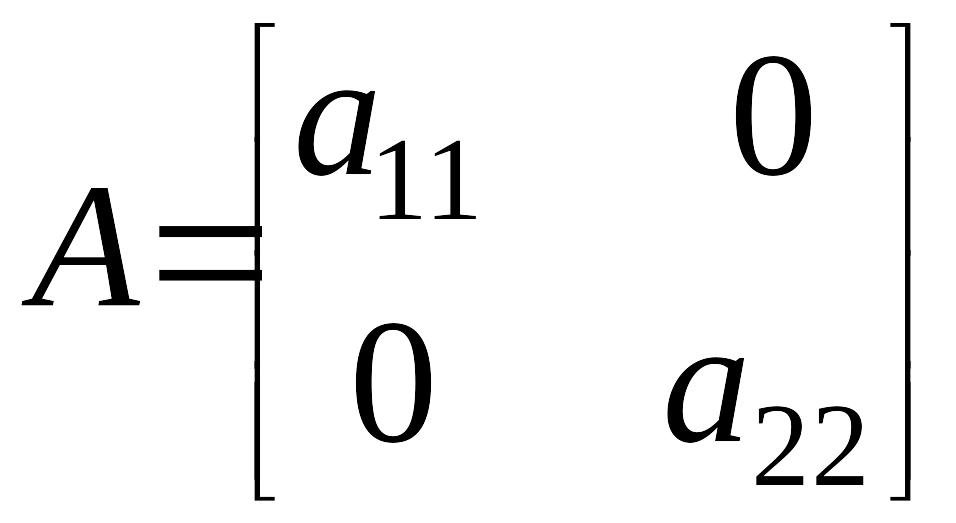, (5)

а характеристическое уравнение (3)

. (6)

Из уравнения (6) следует, что корни характеристического уравнения равны

, . (7)

Следовательно, коэффициенты и динамики системы (4) в этом случае являются корнями характеристического уравнения системы дифференциальных уравнений (4). Тогда систему уравнений (4) можно переписать следующим образом

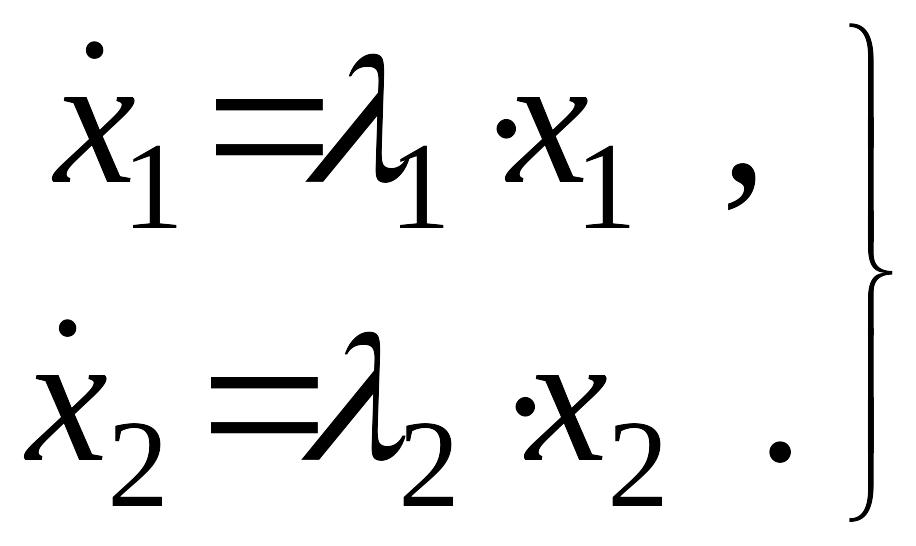(8)

Форма записи уравнений динамики системы управления в виде (8) называется канонической диагональной формой (матрица динамики системы – диагональная)

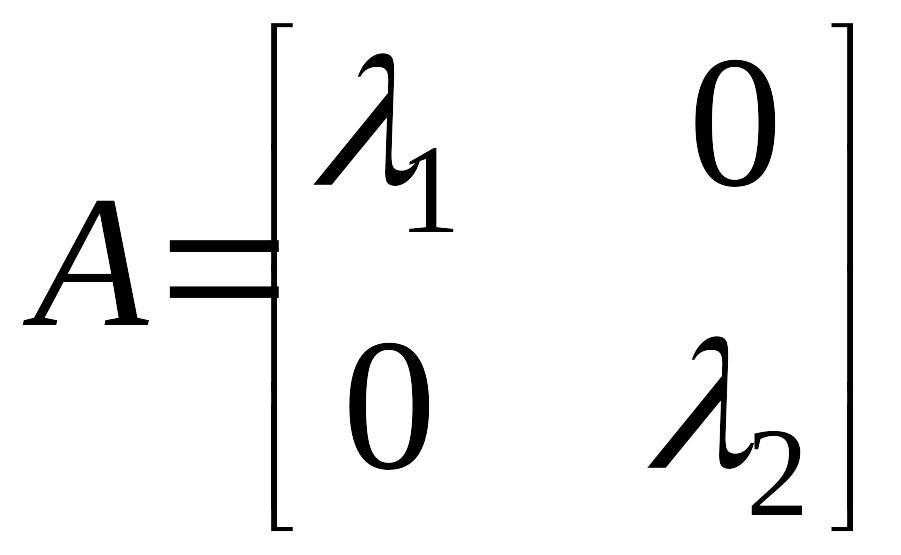, (9)

Из уравнений (8) получим дифференциальные уравнения фазовых траекторий

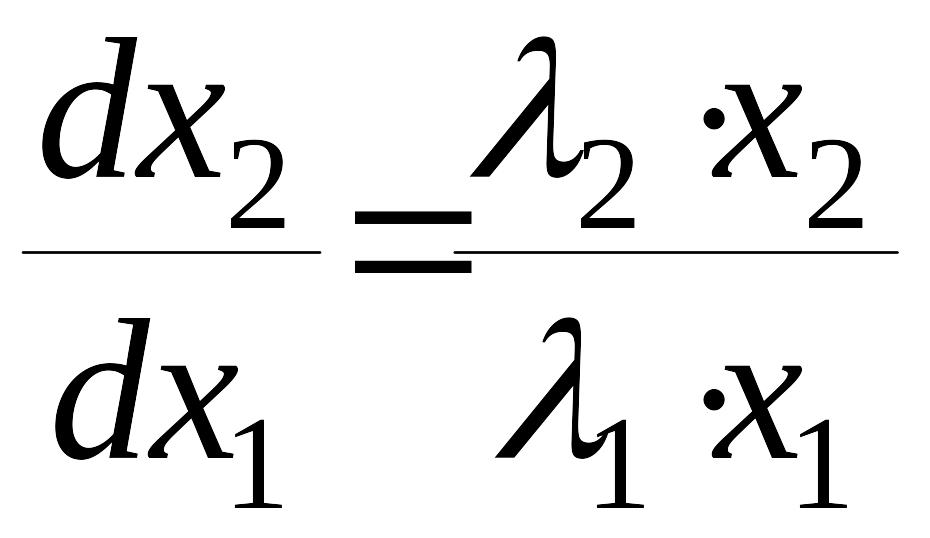. (10)

Это линейное дифференциальное уравнение с разделяющимися переменными. Решая его, последовательно получаем

,

,

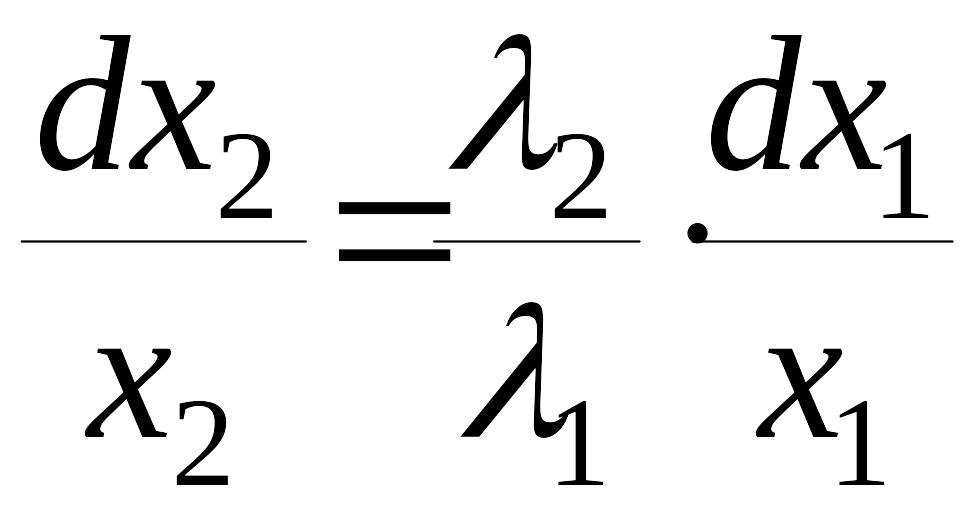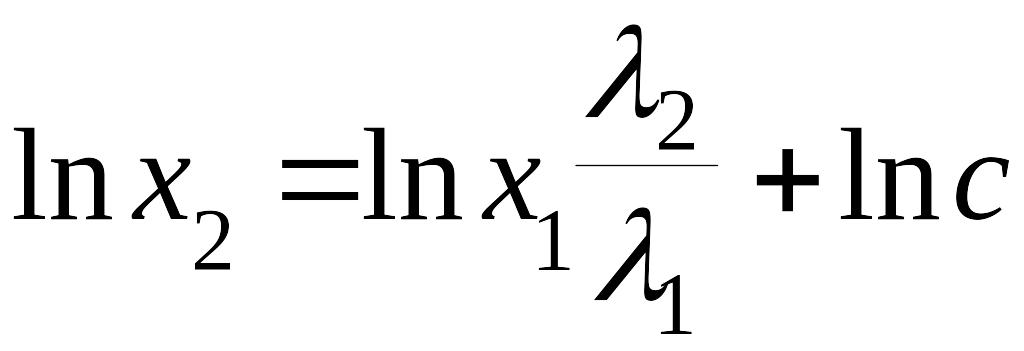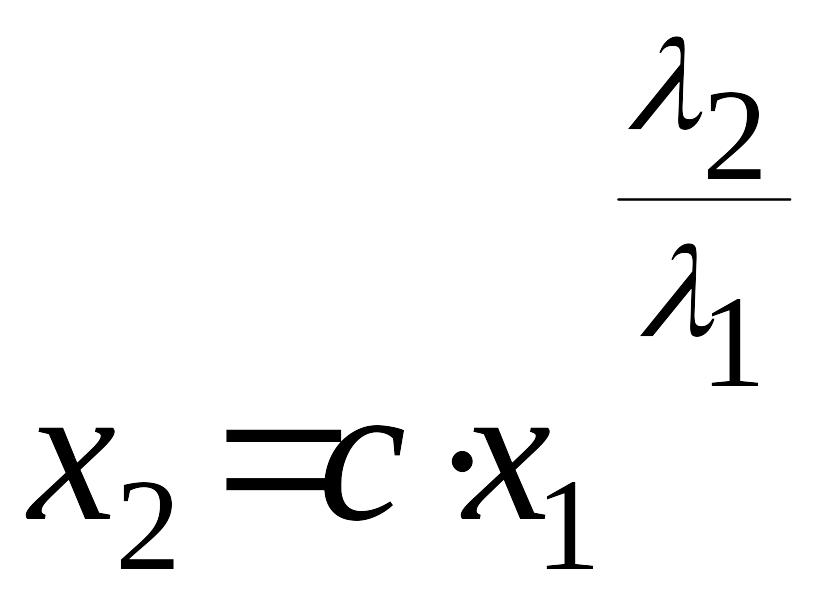. (11)

Получили в явном виде уравнения фазовых траекторий. Так как по условию корни характеристического уравнения действительны, различны и одного знака ( ), то это – уравнение парабол.

Есть ли среди фазовых траекторий траектории, которые являются прямыми, проходящими через начало координат (особую точку)?

Пусть – уравнение прямой, проходящей через начало координат, тогда 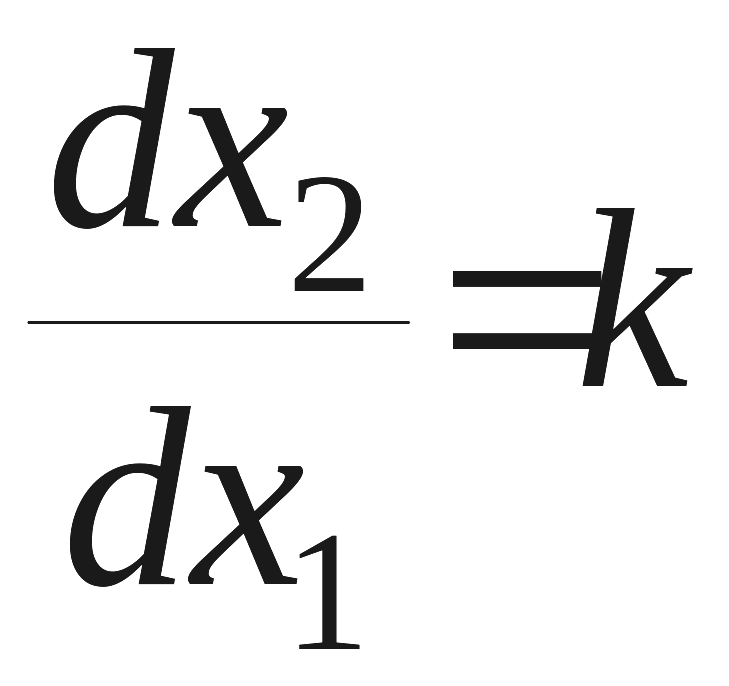. С учетом последних равенств уравнение (10) принимает вид

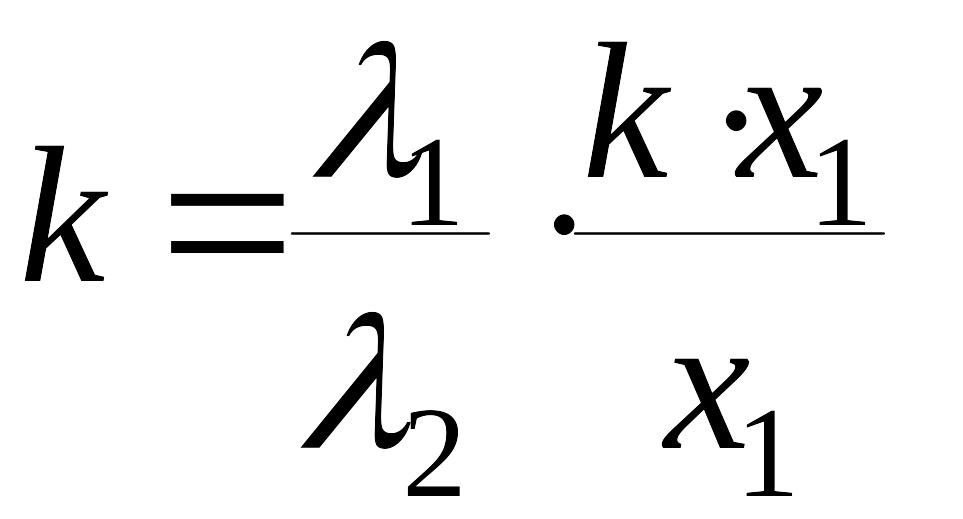
откуда получаем 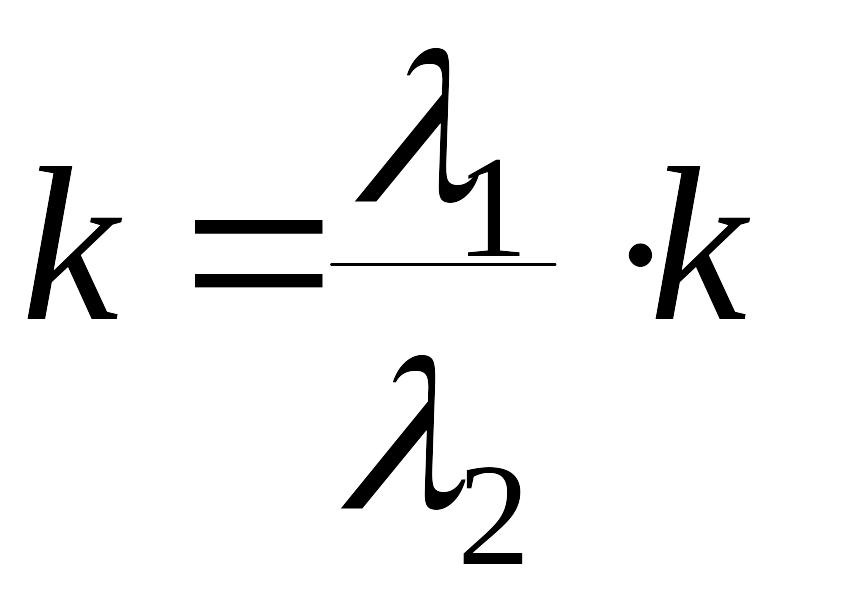, . А это значит, что прямая (координатная ось ) является фазовой траекторией.

Рассмотрим теперь случай, когда уравнение фазовых траекторий имеет вид

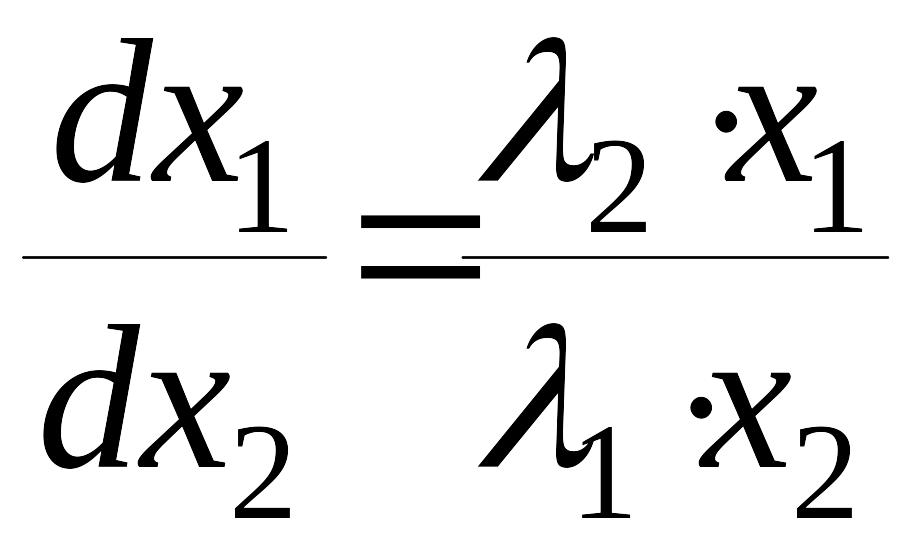(12)

и, аналогично предыдущему, считаем , 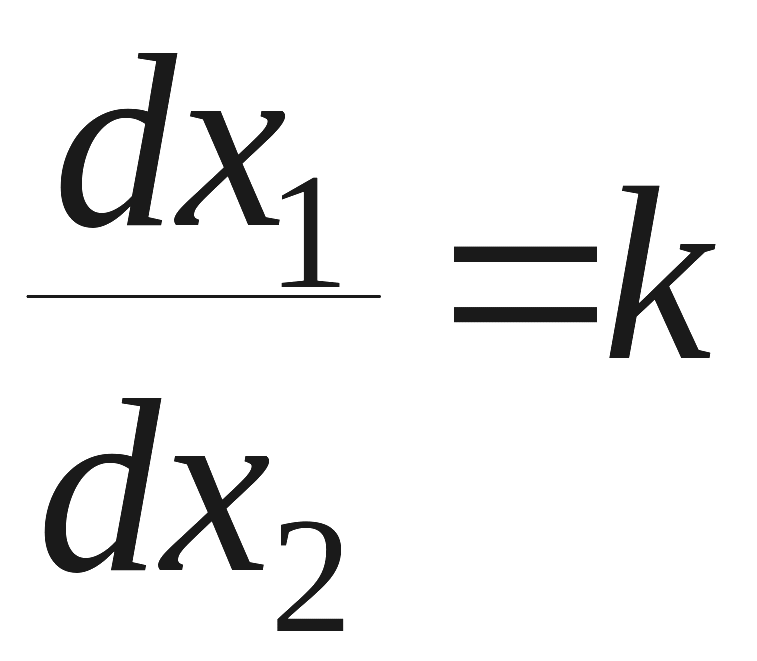. Тогда из (12) получаем

,

, .

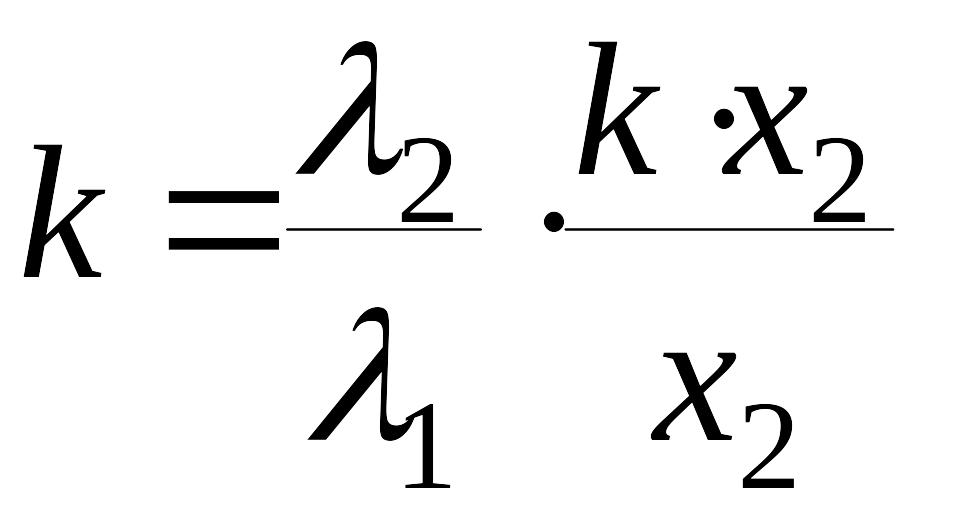Прямая (координатная ось ) также является фазовой траекторией.

Следовательно, есть две прямые, которые являются фазовыми траекториями – это в данном случае – координатные оси.

Итак, фазовый портрет системы имеет следующий вид

Устойчивый узел Неустойчивый узел

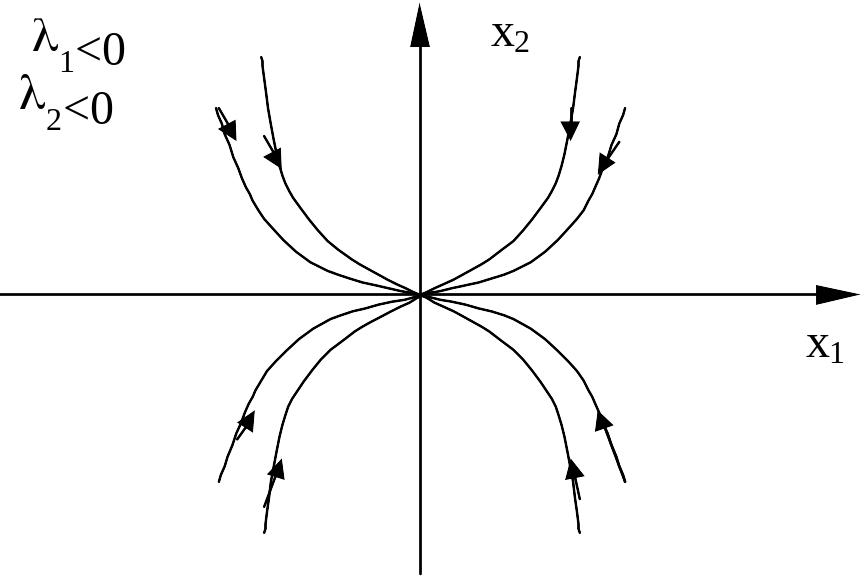
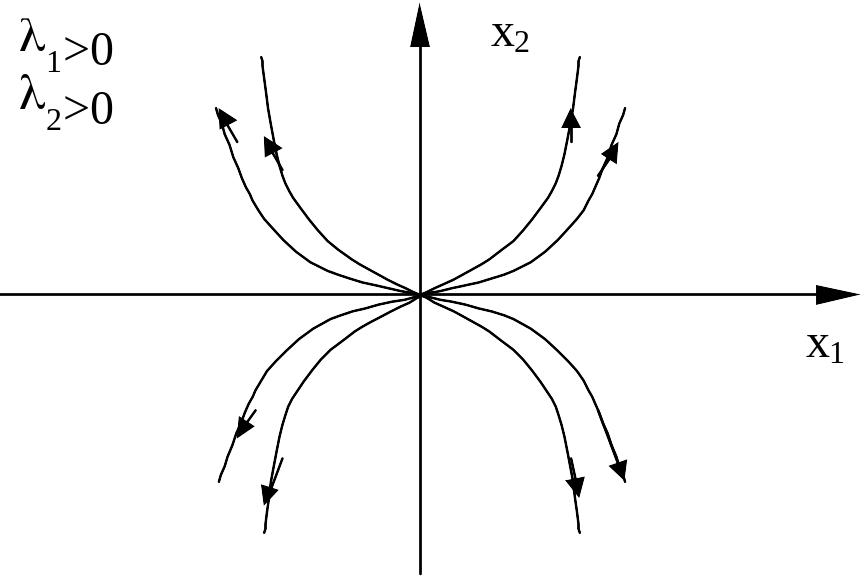
Вывод. Если корни характеристического уравнения для дифференциальных уравнений динамики системы управления действительны, различны и одного знака, то фазовые траектории параболы, а особая точка – узел. При этом, если , - неустойчивый узел, а при , - устойчивый узел.

Как получить уравнения фазовых траекторий и построить фазовый портрет для системы управления, математическая модель которой задана системой уравнений (1)?

Для этой цели Выполним замену переменных по формулам

,

,

или в векторно – матричной форме записи ,где - невырожденная матрица этого преобразования . Матрица составлена из собственных векторов матрицы . Так как справедливо следующее равенство , то система исходных уравнений относительно новых переменных в векторно – матричной форме записи имеет вид . Так как матрица состоит из собственных векторов матрицы и корни ее характеристического уравнения и действительны и различны, то матрица является диагональной, то есть

.

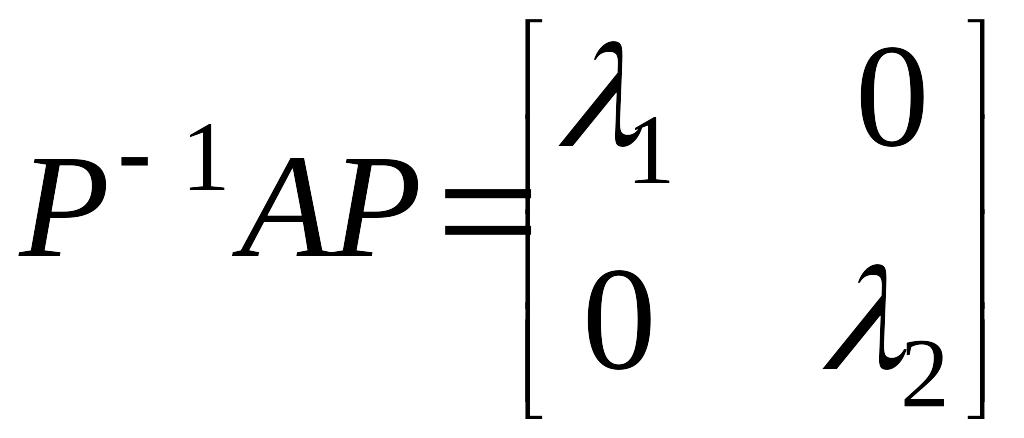Это диагональная форма записи матрицы динамики системы управления, записанной относительно новых переменных состояния и . Следовательно, система уравнений (1) в новых переменных имеет вид

,

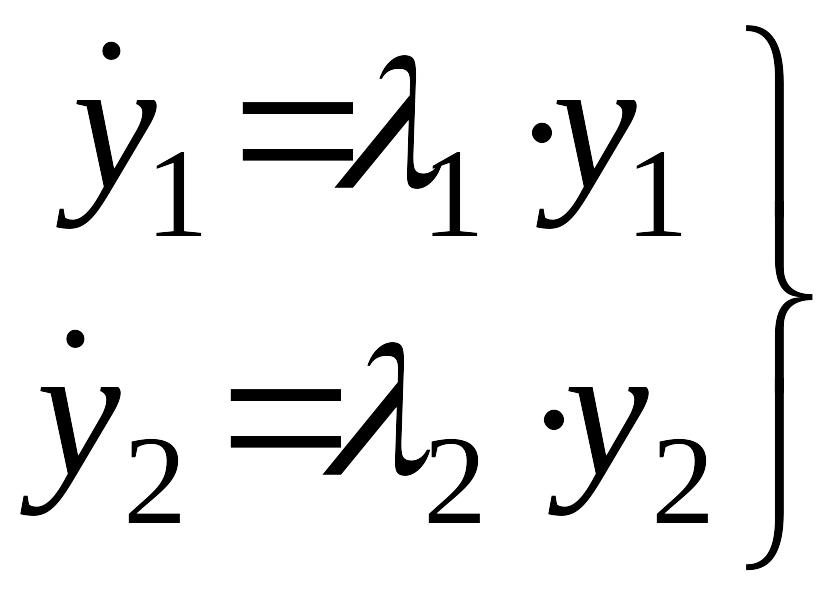аналогичный системе уравнений (8) и уравнение фазовых траекторий системы будет

.

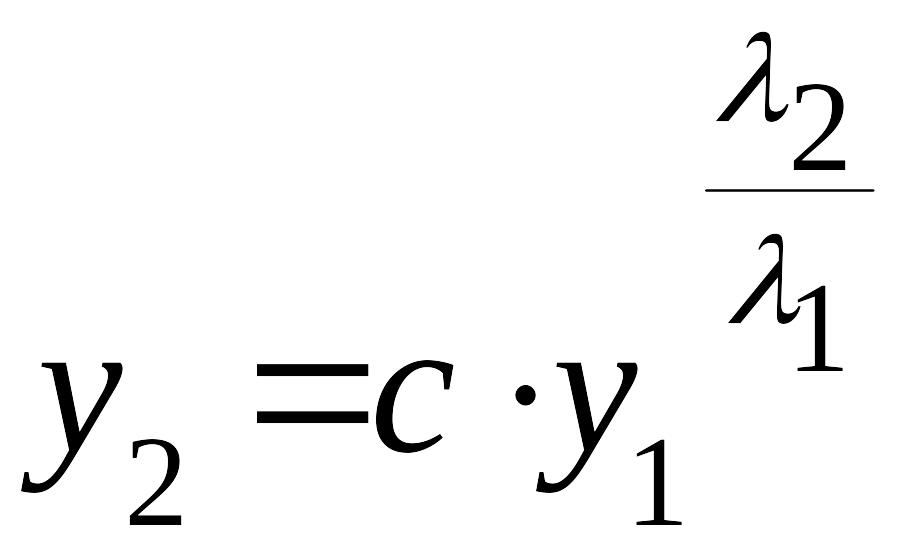Так как , то можно получить уравнения фазовых траекторий относительно старых переменных состояния . Здесь следует отметить, что замена переменных не меняет координаты и тип особой точки.

Какое положение в плоскости займут координатные оси , которые являются фазовыми траекториями? Для этой цели из уравнений (1) получим дифференциальное уравнение фазовых траекторий

.

Так же как и раньше полагаем (прямая, проходящая через начало координат).

, .

.

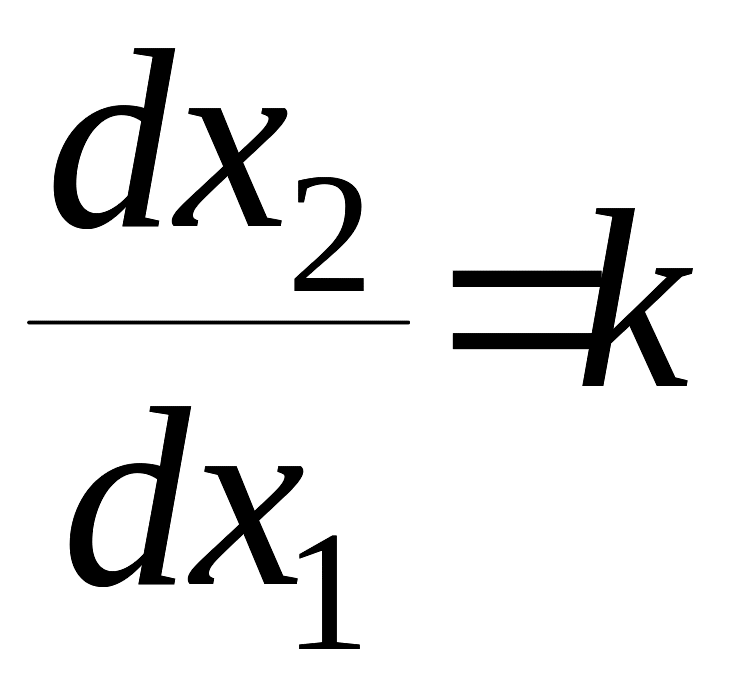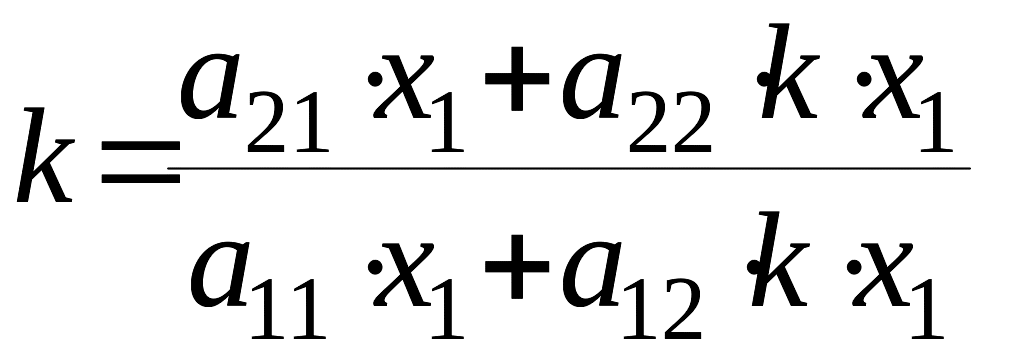Это квадратное уравнение относительно . Решив его – найдем уравнения прямых, которые являются фазовыми траекториями в плоскости (оси координат и ).

Фазовый портрет и переходный процесс на выходе системы (1) имеет вид

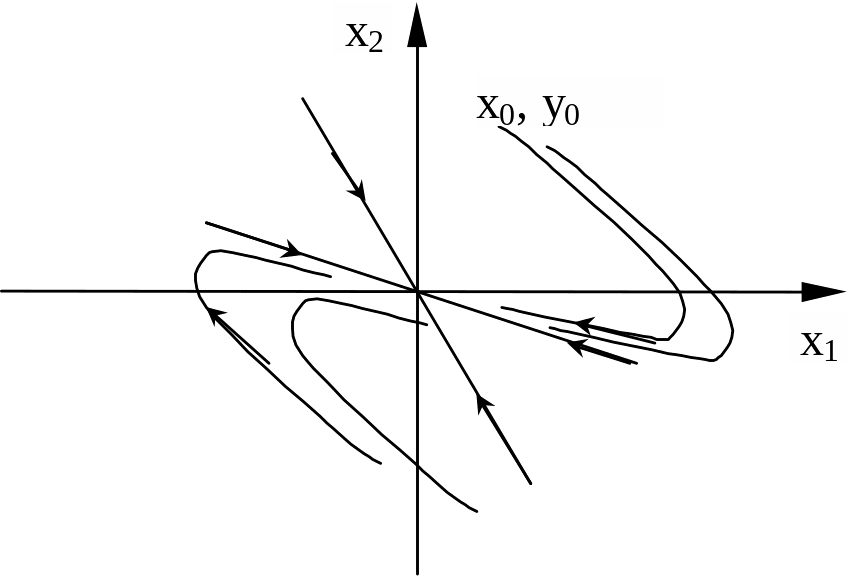
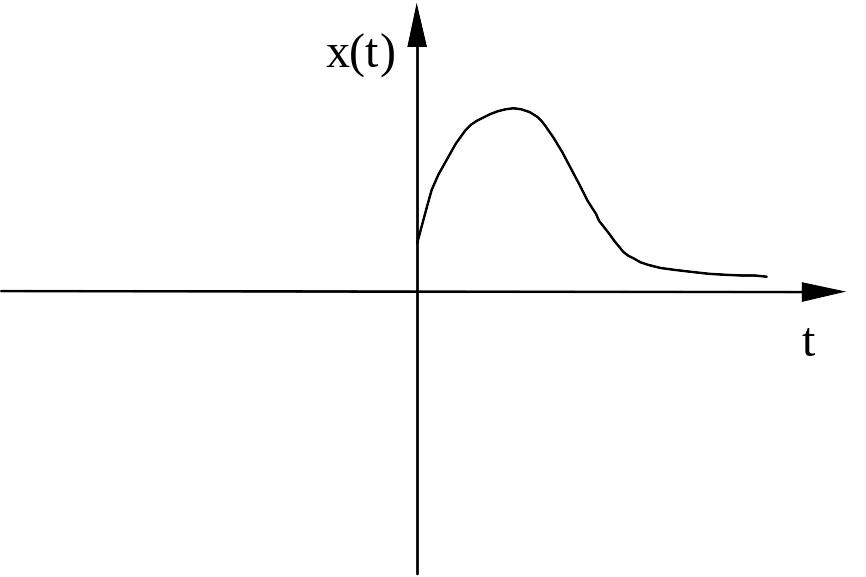
При замене системы координат – изменяется угловая ориентация осей координат.