Лекция 3. Типы особых точек и фазовые портреты линейных систем второго порядка.

Рассмотрим особые точки и фазовые портреты линейных систем, математическими моделями которых являются дифференциальные уравнения вида

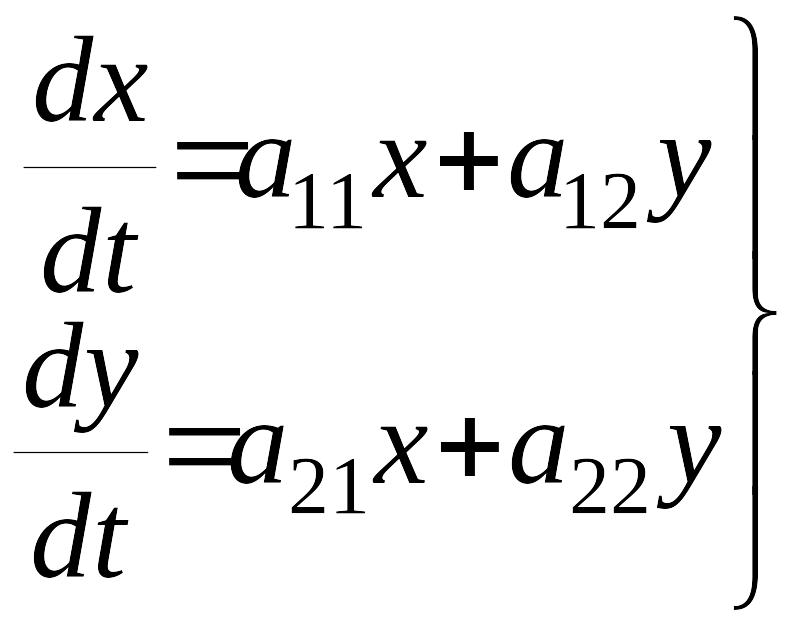. (1)

Определим координаты особой точки. Для этого надо решить систему линейных алгебраических уравнений

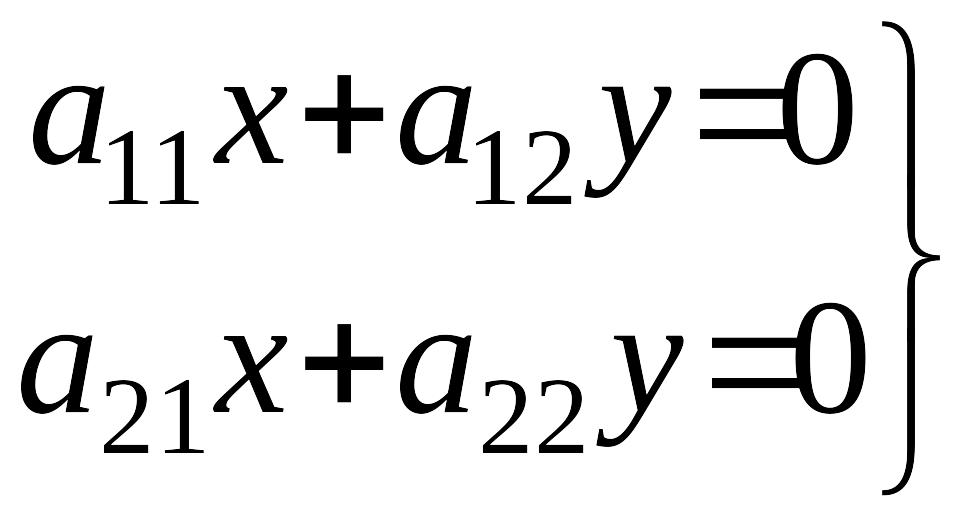(2)

относительно неизвестных и . При условии, что матрица

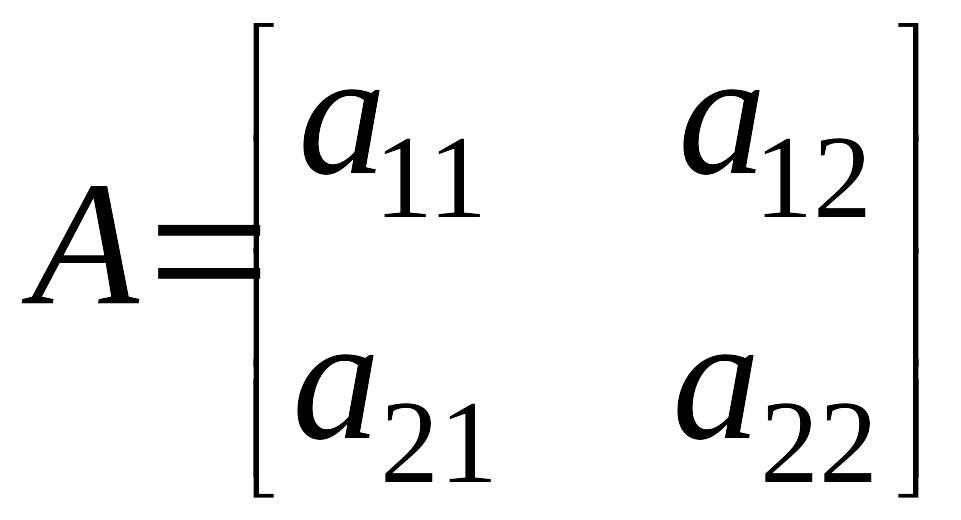
невырождена, т.е. , система линейных уравнений (2) имеет единственное решение , . На фазовой плоскости это соответствует началу координат. Следовательно, линейная система имеет единственную особую точку, которая совпадает с началом координат фазовой плоскости .

Дифференциальное уравнение для фазовых траекторий имеет вид

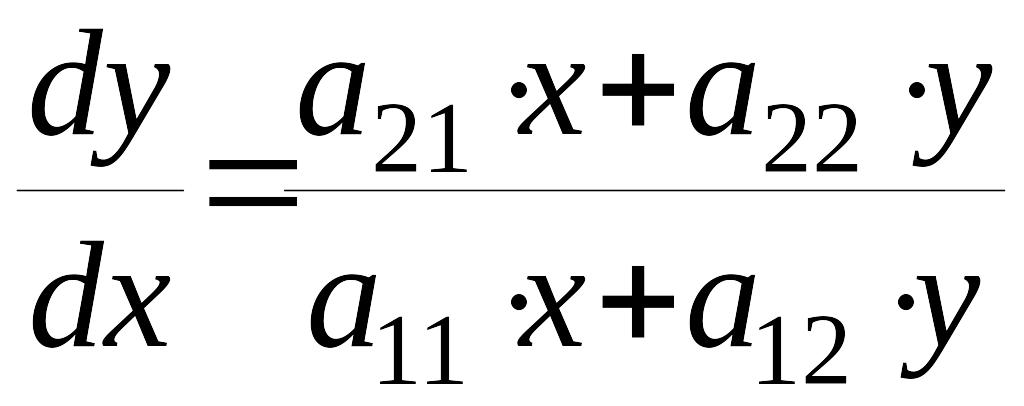(3)

Замечание. Линейное дифференциальное уравнение второго порядка

(4)

можно привести к виду (1) следующим образом. Введем обозначения , тогда . Разрешим уравнение (4) относительно старшей производной

.

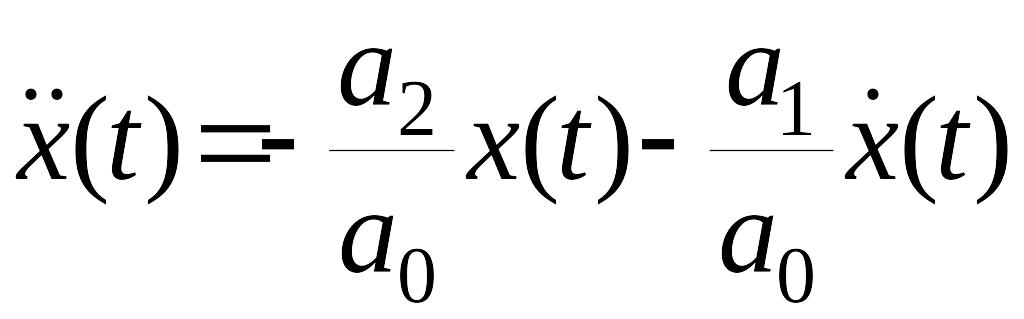Тогда с учетом принятых обозначений имеем

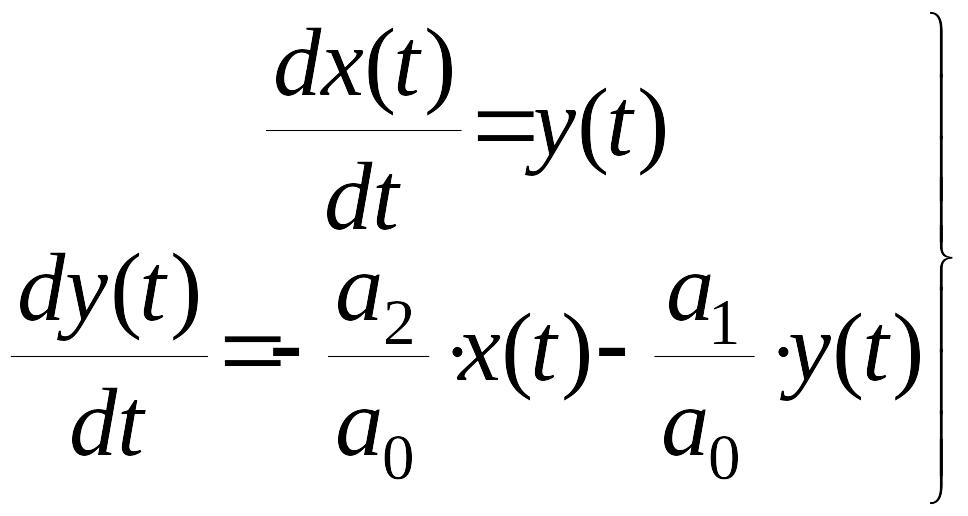. (5)

Сравнивая (1) и (5), видим, что

.

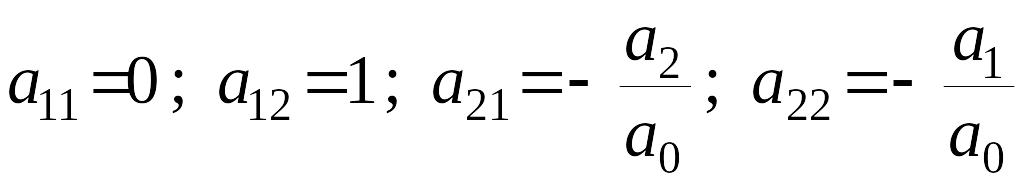Лекция 4. Способы построения фазовых портретов нелинейных систем по уравнениям первого приближения.

1. Аналитические методы.

2. С помощью ЭВМ.

Аналитические методы позволяют в явном виде получать уравнения фазовых траекторий. Здесь возможны следующие основные алгоритмы.

Алгоритм 1. Получив решения уравнений (1) как функции времени и начальных условий , , исключают из последних равенств время . В результате чего получают уравнения фазовых траекторий в явном виде.

Алгоритм 2. Непосредственное интегрирование дифференциальных уравнений фазовых траекторий

Этому предшествует, как правило, преобразование исходной системы к канонической форме записи системы уравнений.

Использование ЭВМ. Это универсальный численный метод пригодный как для уравнений первого приближения, так и для исходных нелинейных уравнений.

1. Численным методом интегрируется система уравнения

,

.

2. Запоминается таблица в виде

…	…	…

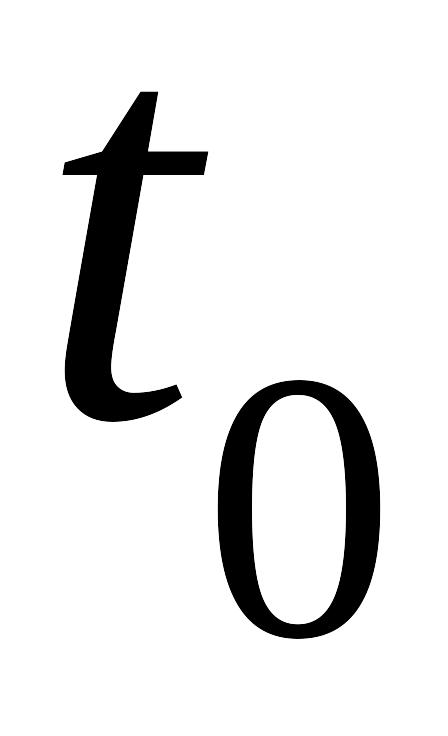
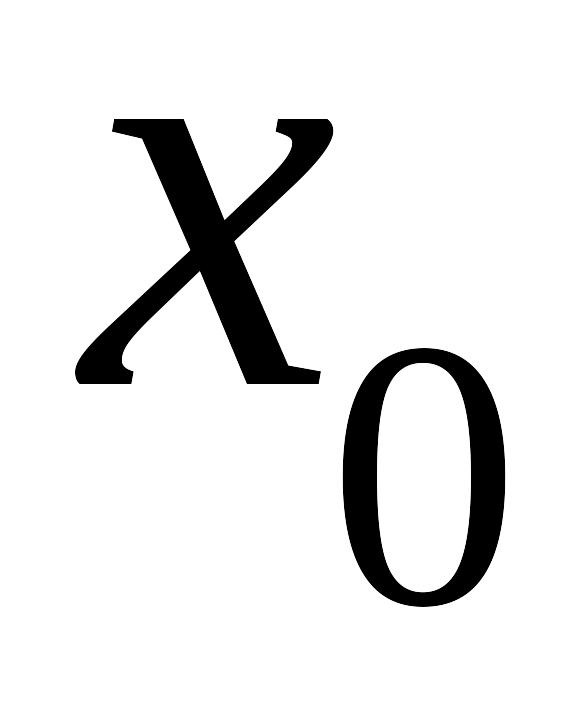
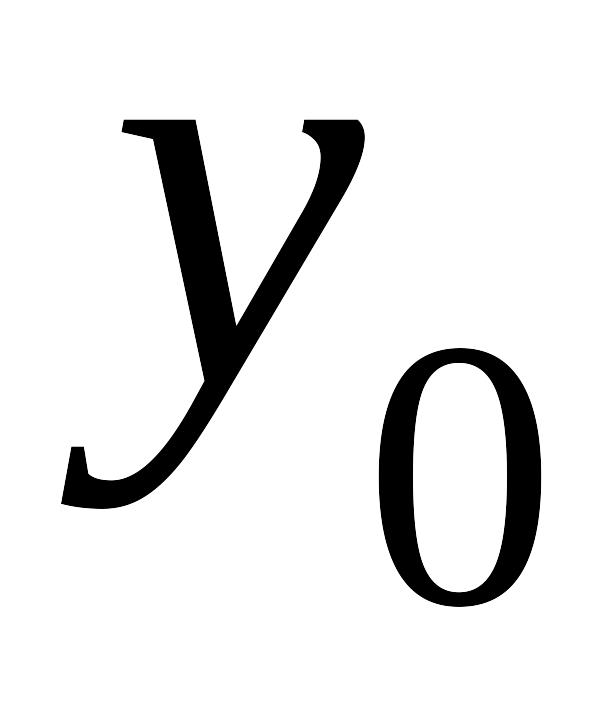
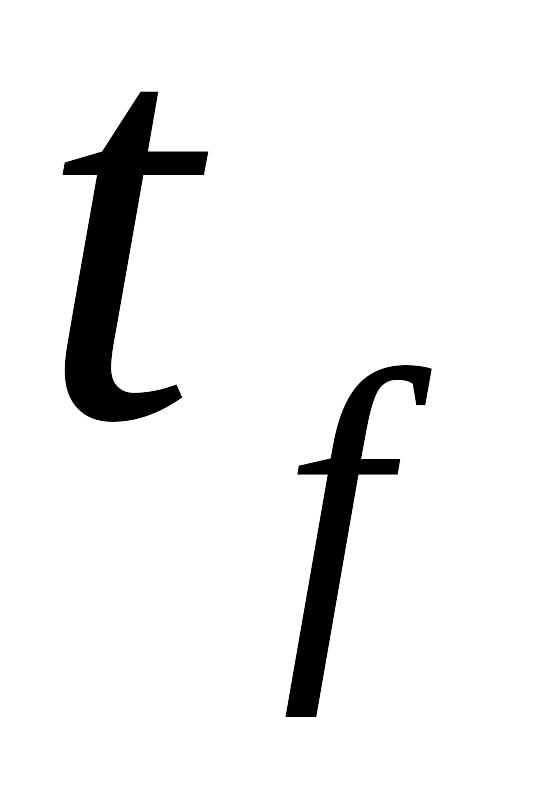
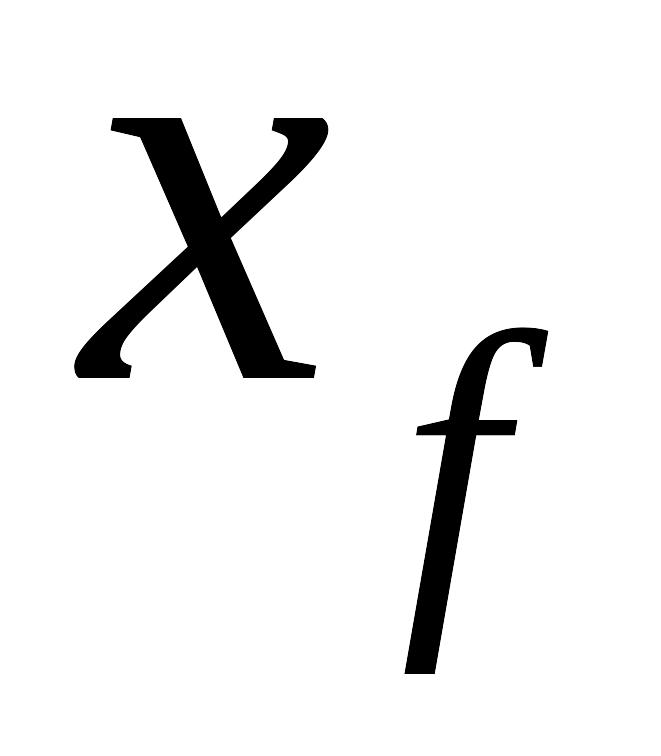
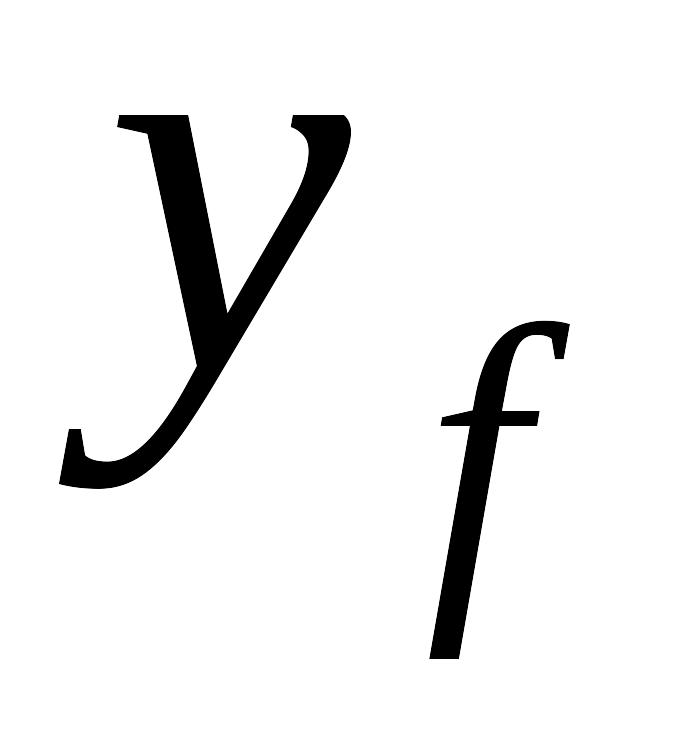
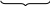
График

3. Строится график, где по оси абсцисс откладываются 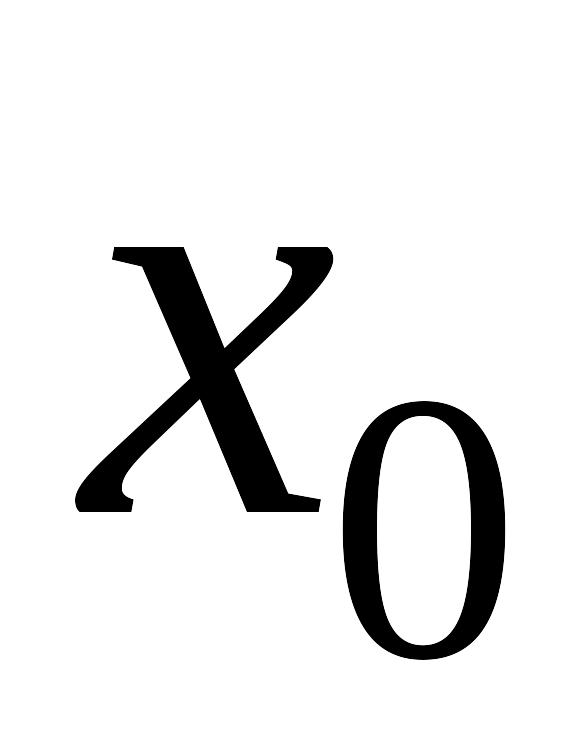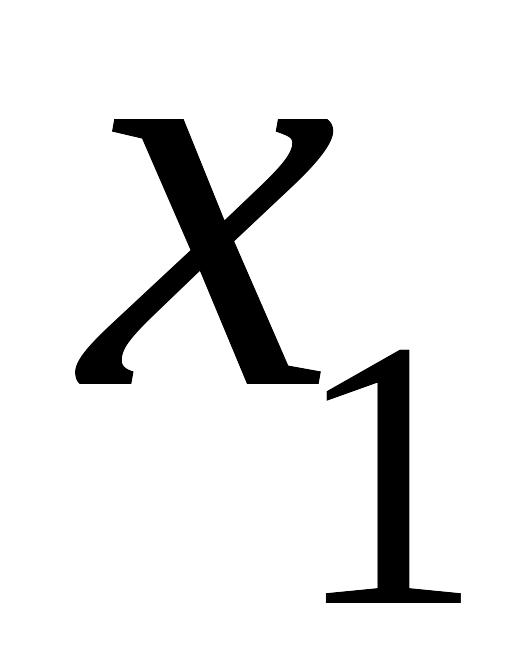значения , , … , ,а по оси ординат – значения , , … , .

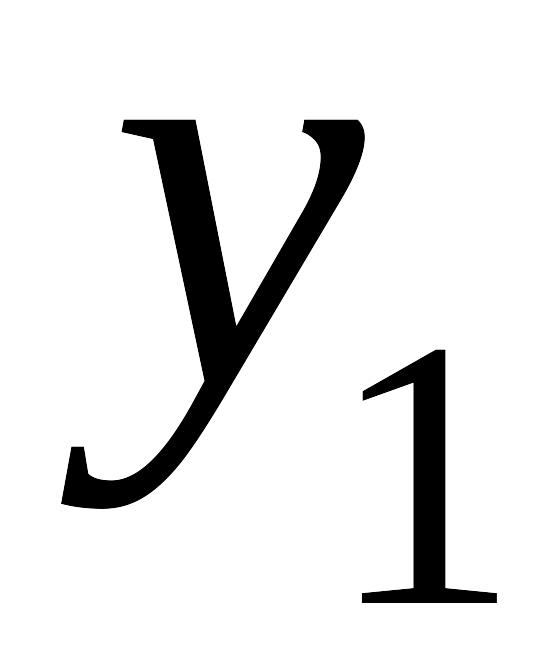В зависимости от корней характеристического уравнения линейной системы различают следующие типы особых точек.