Задание к срсп №5 Тема: Дуобинарное упражнение

Соберите систему:

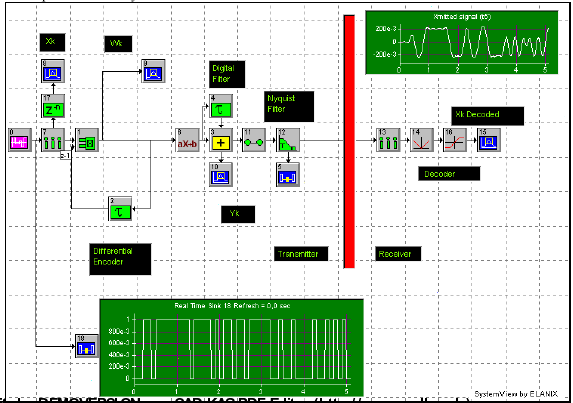
Рисунок

File name: Duobinary_ru.svu

Title: Duobinary.svu

System Time:0 - 5,11e+0 sec, dT=1,0e-2 sec, Sample Rate=1,00e+2 Hz,

Samples=512, Loops=1

Token Attribute Type Parameters

0 Source PN Seq Amp = 500e-3 v, Offset = 500e-3 v, Rate = 10 Hz, Levels =

2, Phase = 0 deg, Max Rate = 100 Hz

1 Operator XOR Threshold = 500e-3, True = 0, False = 1, Max Rate = 10

Hz

2 Operator Delay Non-Interpolating, Delay = 100e-3 sec, = 1,0 smp, Output 0

= Delay , Output 1 = Delay - dT t1 , Max Rate (Port 1) = 10 Hz

3 Adder - - - -

4 Operator Delay Non-Interpolating, Delay = 100e-3 sec, = 1,0 smp, Output 0

= Delay t3 , Output 1 = Delay - dT , Max Rate (Port 0) = 10 Hz

5 Sink Real Time Input from t12 Output Port 0, Max Input Rate = 100 Hz

6 Function Poly -1+(2x), Max Rate = 10 Hz

7 Operator Sampler Non-Interp Right, Rate = 10 Hz, Aperture = 0 sec,

Aperture Jitter = 0 sec, Max Rate = 10 Hz

8 Sink Analysis Input from t17 Output Port 0, Max Input Rate = 10 Hz

9 Sink Analysis Input from t1 Output Port 0, Max Input Rate = 10 Hz

10 Sink Analysis Input from t3 Output Port 0, Max Input Rate = 10 Hz

11 Operator Hold Zero, Gain = 1, Out Rate = 100 Hz, Max Rate = 100 Hz

12 Operator Linear Sys Comm Sin(t)/t FIR, Symbol Rate = 10 Hz, Decimate

By 1, Quant Bits = None, Taps = 81, Init Cndtn = 0, DSP Mode Disabled, Max

Rate = 100 Hz

13 Operator Sampler Non-Interp Right, Rate = 10 Hz, Aperture = 0 sec,

Aperture Jitter = 0 sec, Max Rate = 10 Hz

14 Function Rectify Zero Point = 0 v, Max Rate = 10 Hz

15 Sink Analysis Input from t16 Output Port 0, Max Input Rate = 10 Hz

16 Function Limiter Max Input = ±0 v, Max Output = ±1 v, Max Rate = 10 Hz

17 Operator Smpl Delay Delay = 4 samples, = 400e-3 sec, Attribute = Passive,

Initial Condition = 0 v, Fill Last Register, Output 0 = Delay t8 , Output 1 = Delay

- dT , Max Rate (Port 0) = 10 Hz

18 Sink Real Time Input from t0 Output Port 0, Max Input Rate = 100 Hz

Предварительное кодирование

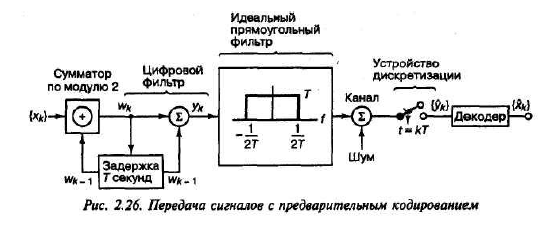
Предварительное кодирование выполняется посредством первоначального дифференциального кодирования бинарной последовательности {хк} в новую бинарную последовательность {wk}, для чего используется выражение

где символ «» представляет сложение двоичных цифр по модулю 2 (эквивалентно операции исключающего ИЛИ). Сложение по модулю 2 имеет следующие правила.

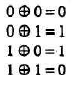
Затем двоичная последовательность {wt} преобразовывается в последовательность биполярных импульсов, и операция кодирования проходит так же, как было показано в примере 2.4. В то же время, как показано ниже, в примере 2.5 при выполнении предварительного кодирования процесс обнаружения отличается от обнаружения в обычной двубинарной схеме. Схема предварительного кодирования показана на рис. 2.26; стоит обратить внимание на то, что сложение по модулю 2, дающее предварительно кодированную последовательность {wk}, выполняется над двоичными цифрами, а цифровая фильтрация, результатом которой является

последовательность {ук}, — над биполярными импульсами.

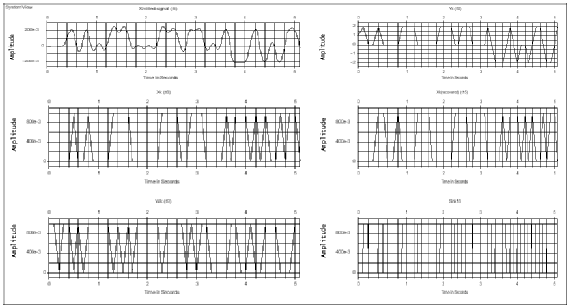
Пример 2.5. Двубинарное предварительное кодирование

Проиллюстрируем правила двубинарного кодирования и декодирования при использовании предварительного дифференциального кодирования, определенного формулой (2.30). Будем использовать ту же последовательность {хк}, что и в примере 2.4.

Решение

Последовательность двоичных цифр 0 0 1 0 1 1 0

{хк}

Предварительно кодированная 0 0 1 1 0 1 1

последовательность wk = хк Ф wk-1

Биполярная последовательность {wk} -1 -1 +1 +1 -1 +1 +1

Правило кодирования: ук = wk + wk-1 -2 0 +2 0 0 +2

Правило декодирования: Если y’k = 2 , то x’k = двоичный

нуль

Если у’k = 0, то х’k = двоичная единица

Декодированная бинарная

последовательность {хк} 0 1 0 1 1 0

Предварительное дифференциальное кодирование позволяет

декодировать последовательность {у’} путем принятия решения по каждой принятой выборке отдельно, не обращаясь к предыдущим, которые могут быть ошибочными. Преимущество заключается в том, что при возникновении из-за помех ошибочной цифры ошибка не будет распространяться на другие цифры. Отметим, что первый бит двоичной последовательности {wk}, подвергаемой дифференциальному кодированию, выбирается произвольно. Если бы начальный бит последовательности {wk} был выбран равным 1, а не 0, результат декодирования был бы таким же.

Это упражнение осуществляет предварительное кодирование двубинарной

системы как описано выше

a) Запустите схему с упражнением

b) Поработайте над декодером символов, чтобы проверить критерии

принятия того или иного решения задачи.

Проверьте данные, начиная с Xk до входа фильтра Найквиста.