Самостоятельная работа студентов под руководством преподавателей (срсп). Срсп №1
Тема: Расчет спектральных характеристик периодических сигналов
Задание
Определить спектры амплитуд и фаз периодической последовательности прямоугольных импульсов длительностью τ=t2-t1, периодом Т и амплитудой u0, следующих с частотой ω1=2π/T. Исходные данные для расчета выбираются из Таблицы 1согласно варианту.
Таблица 1
№ варианта |
t1, с |
t2, с |
Т/ |
u0, В |
1 |
0 |
2 |
3 |
6 |
2 |
0 |
3 |
3 |
5 |
3 |
0 |
4 |
3 |
4 |
4 |
0 |
5 |
4 |
3 |
5 |
0 |
6 |
4 |
2 |
6 |
0 |
2 |
4 |
6 |
7 |
0 |
3 |
5 |
5 |
8 |
0 |
4 |
5 |
4 |
9 |
0 |
5 |
5 |
3 |
10 |
0 |
6 |
3 |
2 |
11 |
0 |
2 |
5 |
6 |
12 |
0 |
3 |
4 |
5 |
13 |
0 |
4 |
4 |
4 |
14 |
0 |
5 |
3 |
3 |
15 |
0 |
6 |
3 |
2 |
Вычислить двенадцать первых составляющих ряда Фурье для данной последовательности прямоугольных импульсов и проследить, как их сумма сходится к указанному ряду.
Указания к выполнению
Функция u(t), описывающая такую последовательность импульсов (рисунок 1), может быть задана в виде:
Рисунок 1
Комплексный спектр определяется выражением:
(1)
Амплитуды гармоник, включая постоянную составляющую равную А0/2, определяются из выражения:
,
при k=0,1,2…
(2)
Выбор начала отсчета на величину амплитуды гармоник не влияет. Огибающая спектра амплитуд определяется видом функции:
(3)
при ω=0 получаем A0=2u0τ/T (4)
Характер изменения амплитуд диктуется функцией sinx/x и не зависит от частоты следования импульсов. На частотах, кратных 2π/τ огибающая равна 0.
Н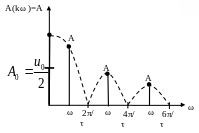
а
рисунке 2 приведена диаграмма спектра
амплитуд для случая T/τ=2,
т.е. ω1=π/τ
Опираясь на формулу (1) и принимая во внимание, что знаки функции Sin(kω1τ/2) чередуются на последовательности интервалов частот Δω=2π/τ, выражение для спектра фаз запишем следующим образом:
φк=kω1(t1+τ/2)-(n-1)π (5)
где n-номер интервала частот Δω=2π/τ, отсчитываемого от ω=0.
Спектр фаз зависит от выбора начала отсчета. Если передний фронт прямоугольного импульса последовательности приходится на начало отсчета времени (t1=0), то на каждом интервале Δω фазы составляющих возрастают линейно.
На рисунке 2 приведена диаграмма спектра фаз для случая T/τ=2, t1=0.
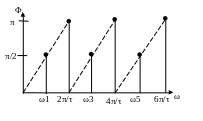
Рисунок 2
Опираясь на рассчитанные составляющие спектров амплитуд и фаз, исходный сигнал можно представить в виде зависимости (ряд Фурье):
(6)
Определим пять первых составляющих ряда Фурье (6) для периодической последовательности прямоугольных импульсов, у которых длительность равна половине периода (Т/=2). Примем также t1=0.
Воспользуемся результатами предыдущих вычислений. По формуле (4) определим постоянную составляющую А0, а по формулам (2) и (5) – амплитуды и фазы первых пяти гармоник. Данные расчетов сведены в таблицу 2. Четные гармоники в таблице не указаны, т.к. они равны 0.
Таблица 2
ωn=kω1 |
φk |
A(kω1) |
Составляющие |
0 |
0 |
u0 |
u(t)=u0/2 |
ω1 |
|
|
u1(t)= u0cos(ω1t- ) |
ω3 |
|
|
u3(t)= u0cos(3ω1t- ) |
ω5 |
|
|
u5(t)= u0cos(5ω1t- ) |
u0
u0
u0
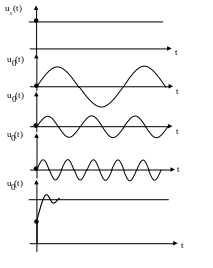
На рисунке 3 показаны составляющие сигнала u(t), а также их результирующая (сумма).
СРСП №2, №3, №4
Тема: «Квантование и дискретизация»
В этом разделе мы будем использовать квантователь из библиотеки функциональных значков SystemView, чтобы квантовать входной сигнал на фиксированное количество битов. Моделирование в предыдущих случаях входные сигналы различных лексем были с точностью плавающей точки, поэтому для большинства целей мы можем предположить, что (заметного) квантования нет.
Задание к СРСП №2
Квантование сигнала
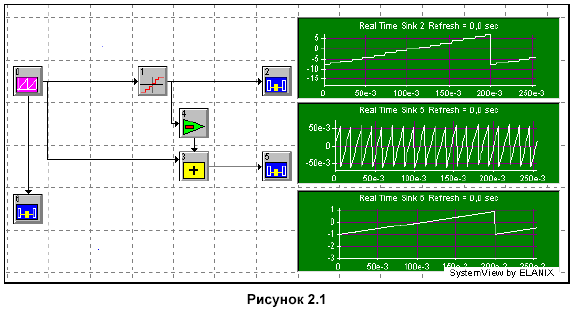
Соберите схему, приведенную на рисунке 2.1.
Установите следующие параметры в системе.
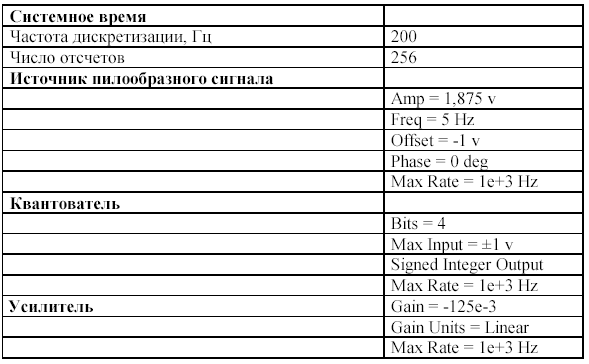
Система
берет (с точностью плавающей точки)
квантованный выходной сигнал генератора
пилообразного сигнала с амплитудой
напряжения 1,875 В и преобразует его в
целое квантованное число. Все источники
выходных сигналов в SystemView, по умолчанию
установлены на точность с плавающей
точкой (исключая, конечно, источники,
которые считываются из файла, которые
могут быть установлены на точность с
фиксированной точкой).
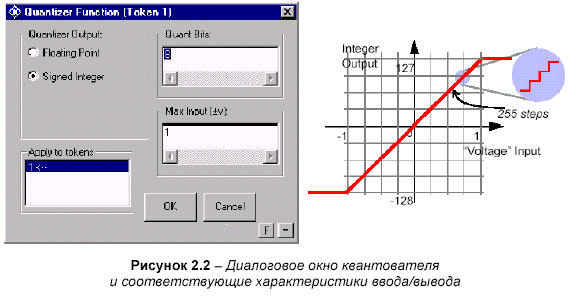
(а) Просмотрите параметры значка 4-х битного квантователя и убедитесь, что имеет входные/выходные характеристики показанные на рисунке 5.2
Обратите внимание, входной квантователь является восьмибитным, поэтому вторичная амплитуда дополнения находится в пределах от -23 до 23, например: -8 до +7.
(б) Запустите систему и затем в окне анализа убедитесь, что значения
выборок такие, как предполагались на выходе квантователя рассмотренного выше. (Не забудьте нажать мерцающую синим цветом
кнопку
«Загрузить обновленные данные блока»
,
чтобы увидеть
обработанные данные только прошедшего процесса моделирования).
(в) Определите погрешность квантования, вычисление которой
осуществляется модулями 3, 4 и 5. Объясните полученные результаты.
(г)
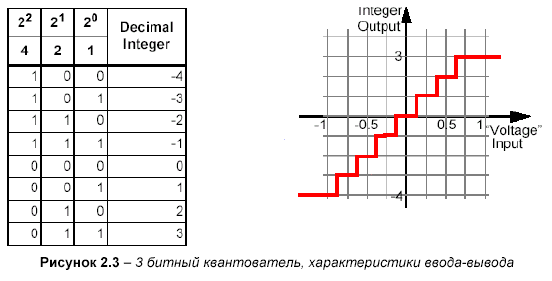
Модифицируйте параметры квантователя
так, чтобы обеспечить трехбитное
квантование (8 уровней как показано на
рисунке 5.3) с таким же ±1 колебанием
напряжения как раньше. Запустите систему
и убедитесь, что результаты такие, как
предполагалось, и совпадают с данными
таблицами, показанными на рисунке 5.3.
(д) Модифицируйте систему так, чтобы амплитуда пилообразного сигнала на входе была равна 2 В. Запустите систему и обратите внимание на эффект «сжимания» ADC. Это происходит потому, что присутствует проблема нелинейности, которая появляется тогда, когда входное напряжение на ADC слишком высокое.
(е) Обратите внимание, что в диалоговом окне параметров квантователя, можно настроить вывод так, что он будет выводиться в форме с плавающей точкой или как целое число. Произвести такую настройку можно при помощи радио-кнопок показанных на рисунке 2.2.
Теперь установите форму вывода «с плавающей точкой», запустите процесс моделирования и объясните то, что теперь показывается на выходе
.
(ж) Измените модуль генератора прямоугольных импульсов на
генератор синусоидальных сигналов (ГСН), запустите систему повторно
при значении выходных напряжений ГСН, равных 1,75, 1,875 и 2,0 В.
Объясните полученные результаты.