Пример. Структурная схема системы автоматического управления имеет вид, показанный на рисунке

, , , .

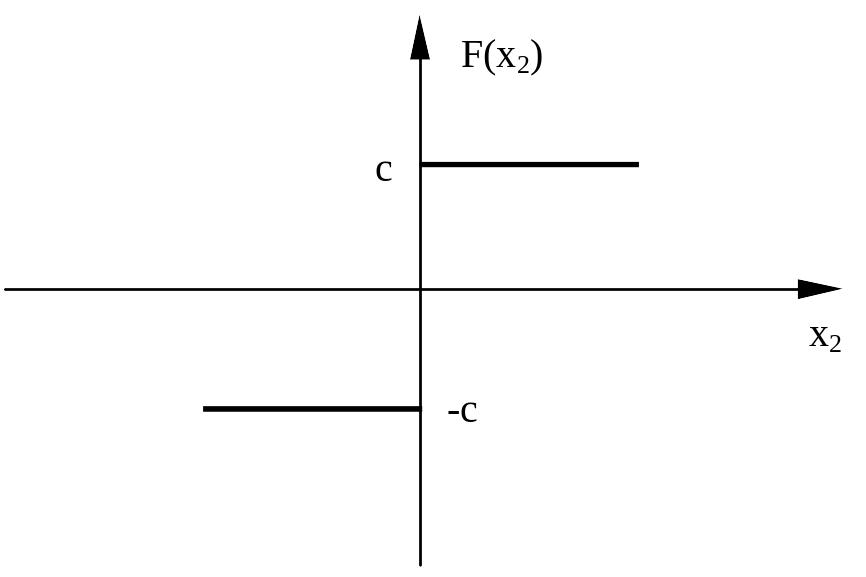
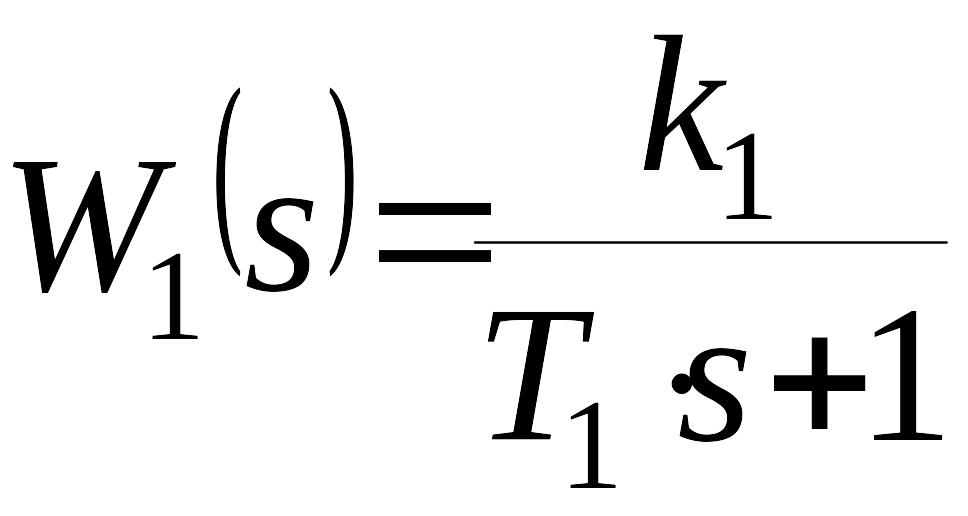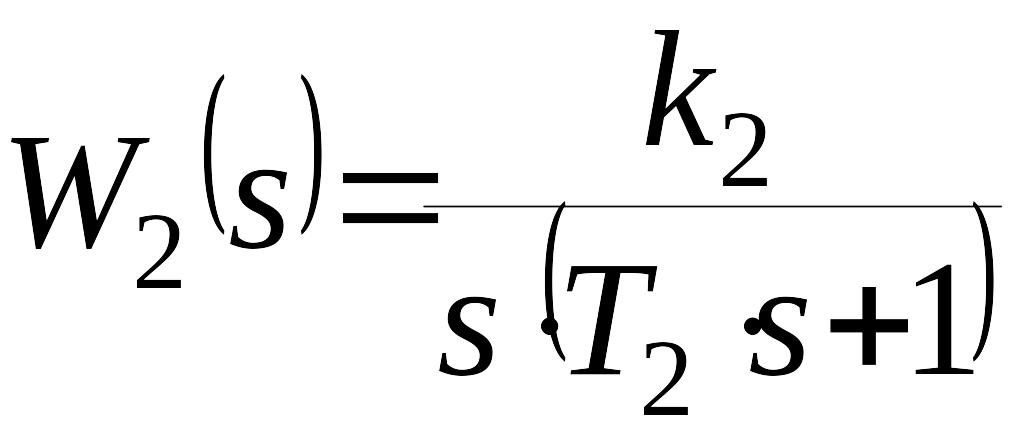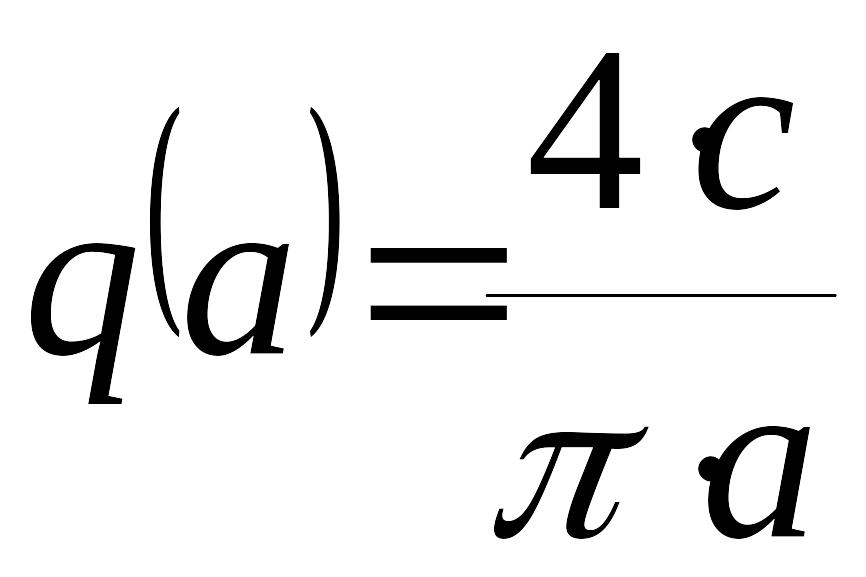Определить параметры возможных периодических процессов в системе.

Решение. В соответствии с выше принятыми обозначениями

, ,

, .

,

.

Структурная схема гармонически линеаризованной системы

y

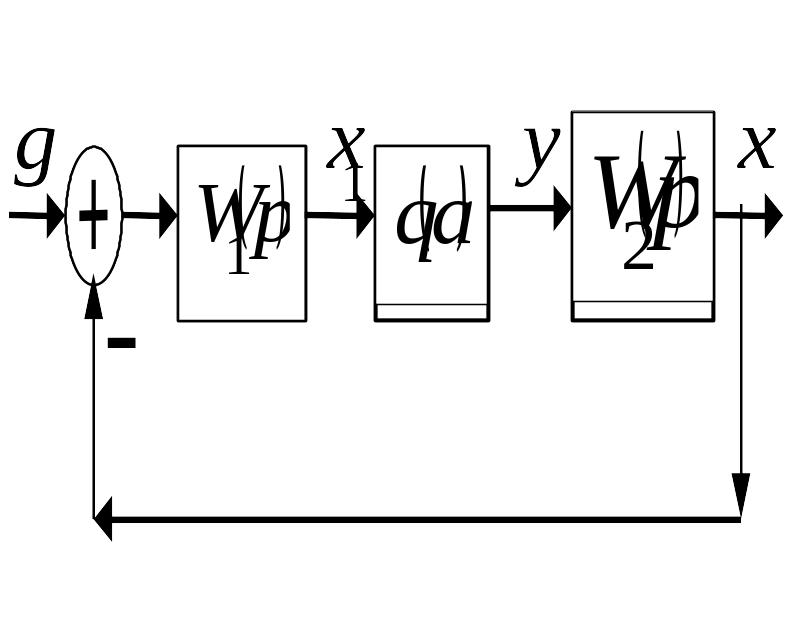
Характеристическое уравнение гармонически линеаризованной системы

,

,

,

.

Выделяем действительную и мнимую части в последнем уравнении и приравниваем их нулю

, .

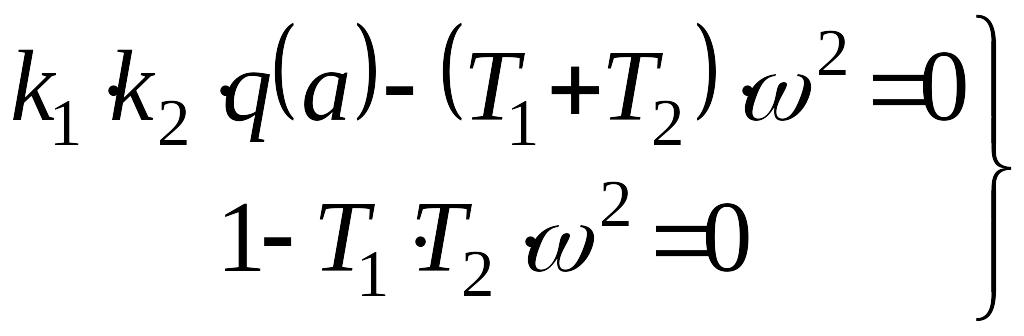Из второго уравнения полученной системы

, ,

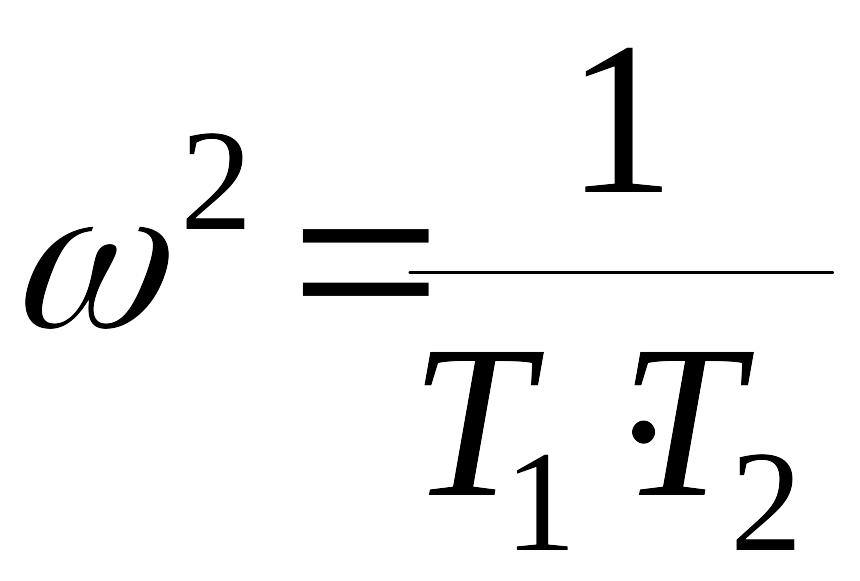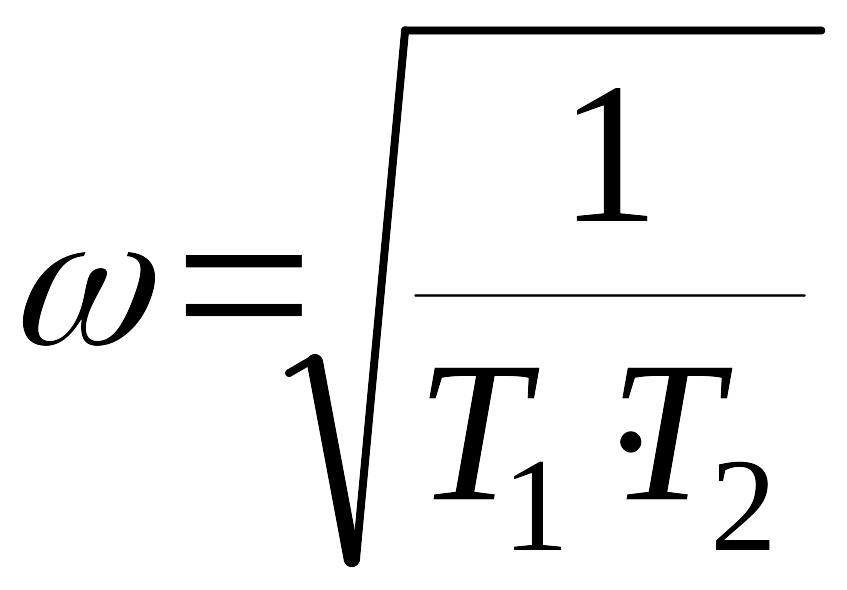из первого уравнения системы

, ,

.

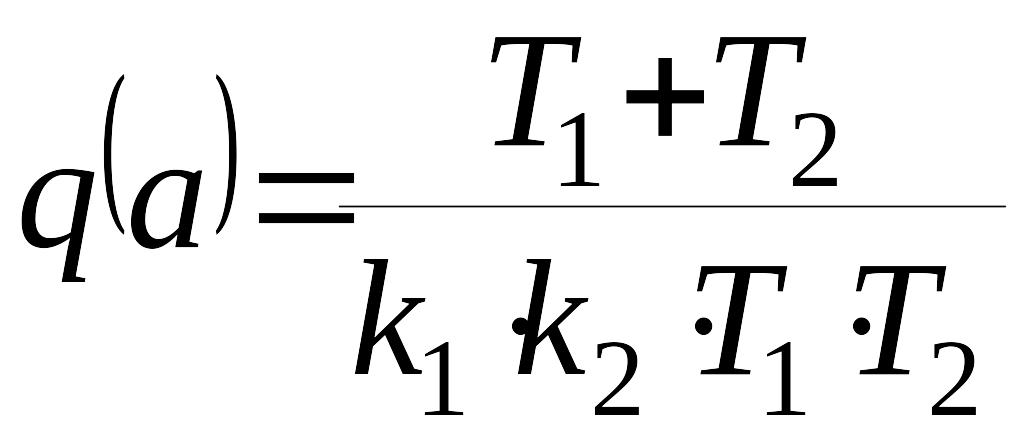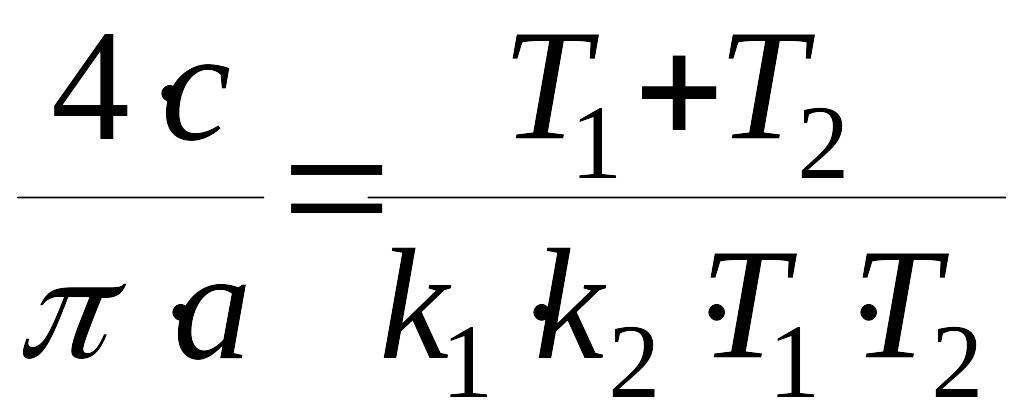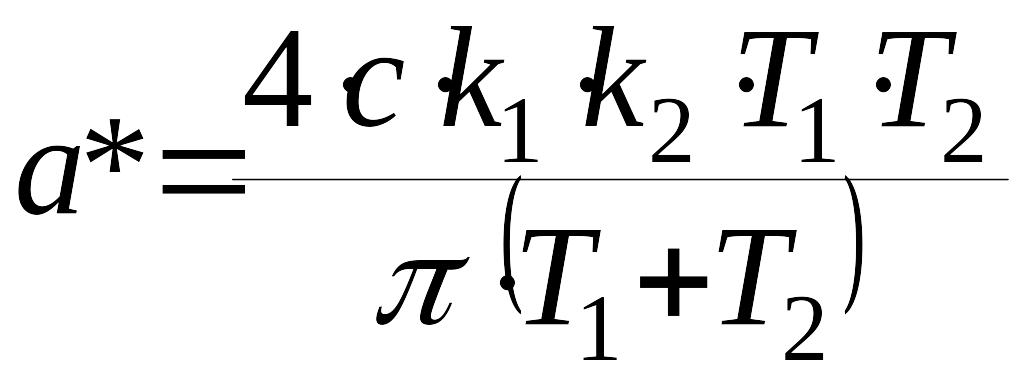Практическое занятие 7. Исследование устойчивости периодического решения.

Пример. Структурная схема системы автоматического управления представлена на рисунке

Определить параметры периодического решения. Исследовать устойчивость периодического решения.

Решение. Гармоническая линеаризация нелинейного звена дает следующие коэффициенты гармонической линеаризации:

, .

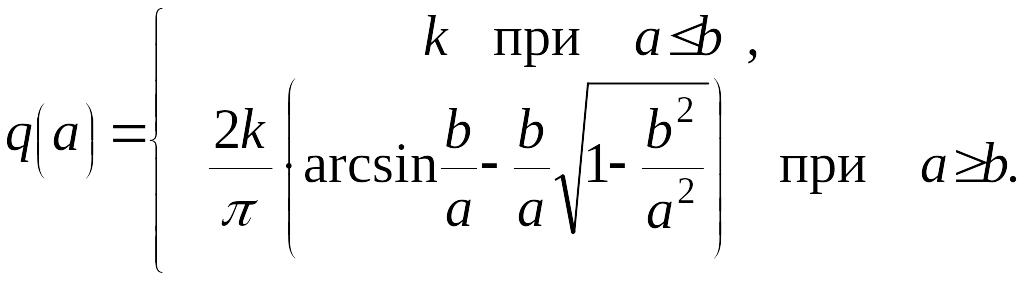Гармонически линеаризованное уравнение замкнутой системы имеет вид

, (1)

Характеристическое уравнение

. (2)

Подстановка в уравнение (2) дает

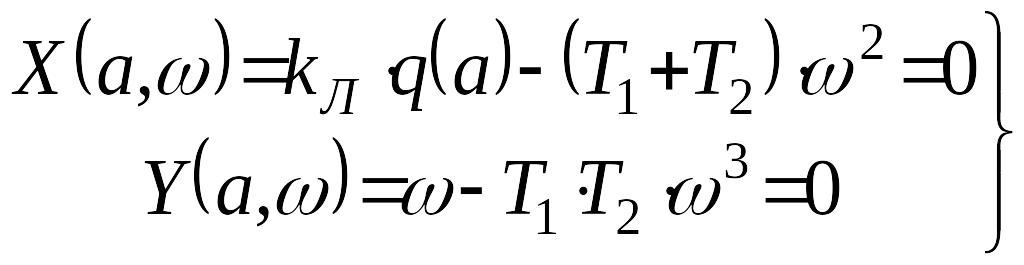. (3)

Из второго уравнения системы (3) получаем частоту периодического решения

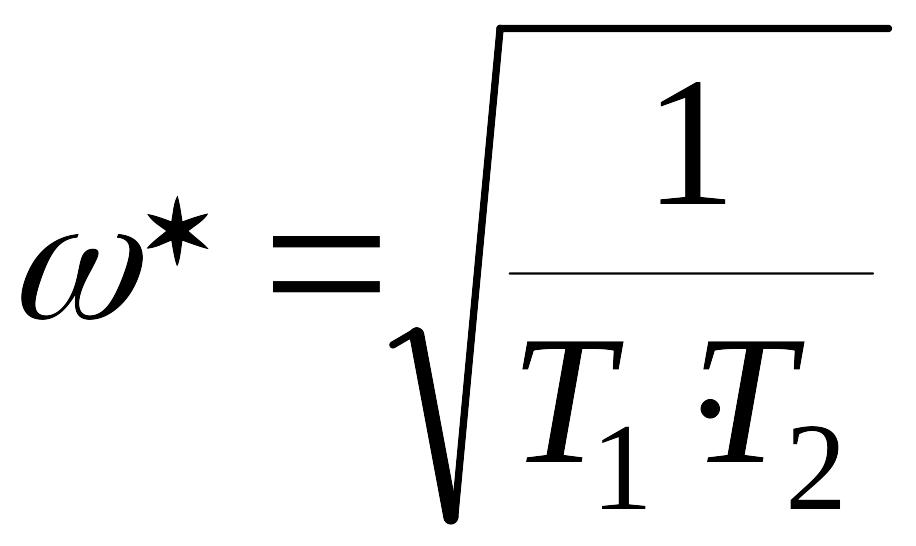, . (4)

Из первого уравнения системы (3) получаем

. (5)

Найти решение (амплитуду периодического решения) можно используя график функции так как показано на рисунке

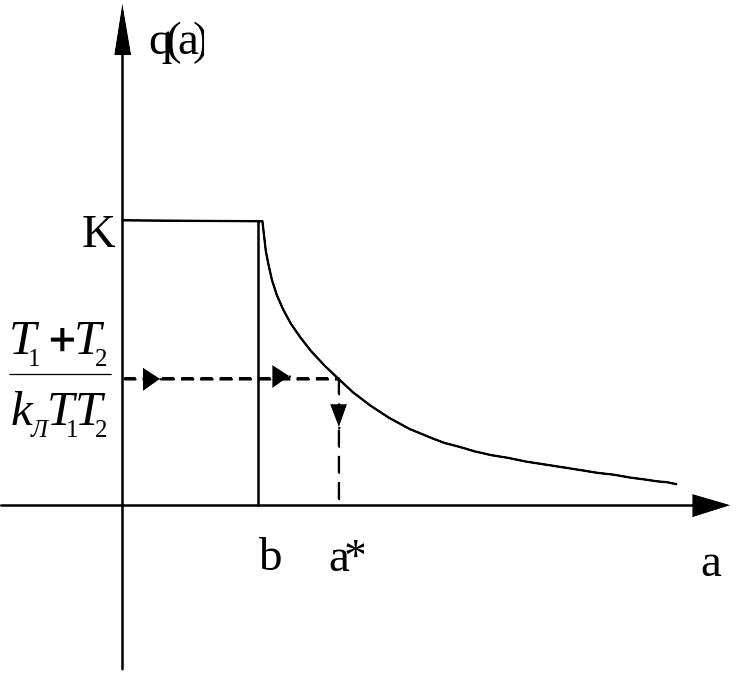
Таким образом, определены параметры периодического решения .

Исследуем устойчивость периодического решения. Для этого надо найти производные и по и при и и исследовать знак выражения

, (*)

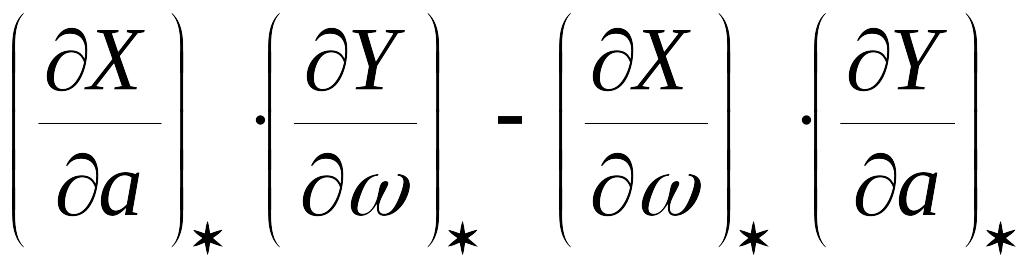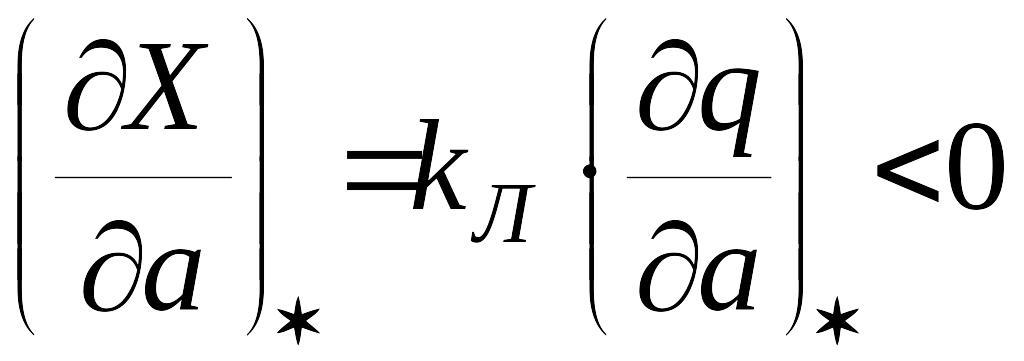это можно установить из графика ,

, ,

.

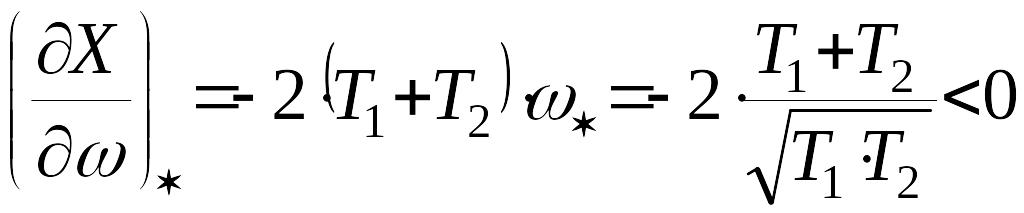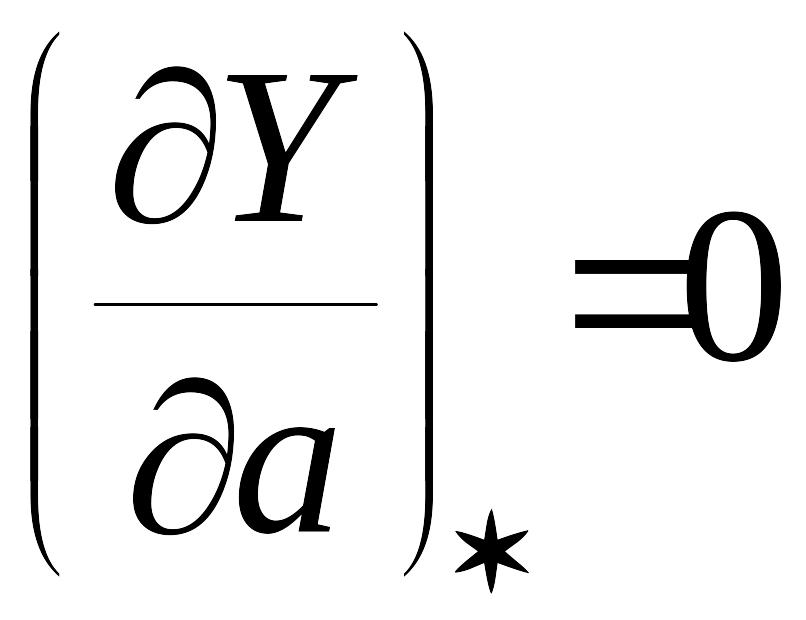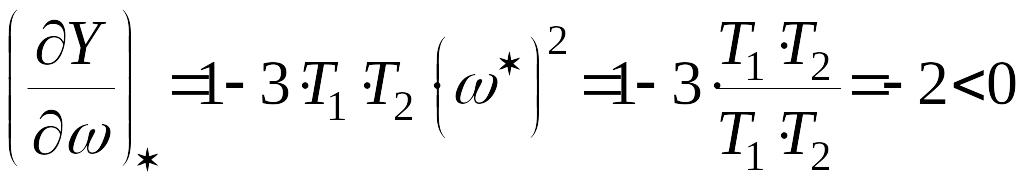Тогда выражение (*) имеет знак

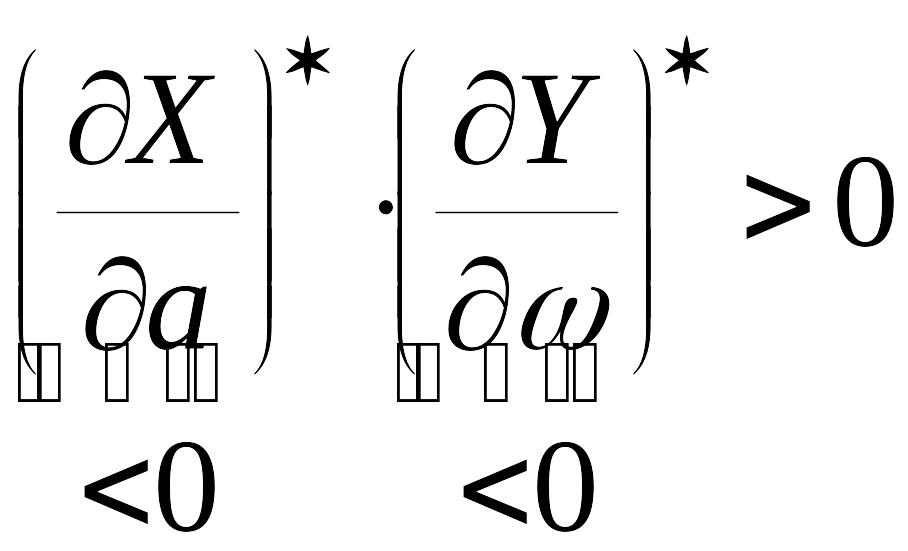
Следовательно, (*) положительно. Проверим второе условие устойчивости периодического решения. Корни этого полинома

должны иметь отрицательные вещественные части. Поделим характеристический полином (2) на

.

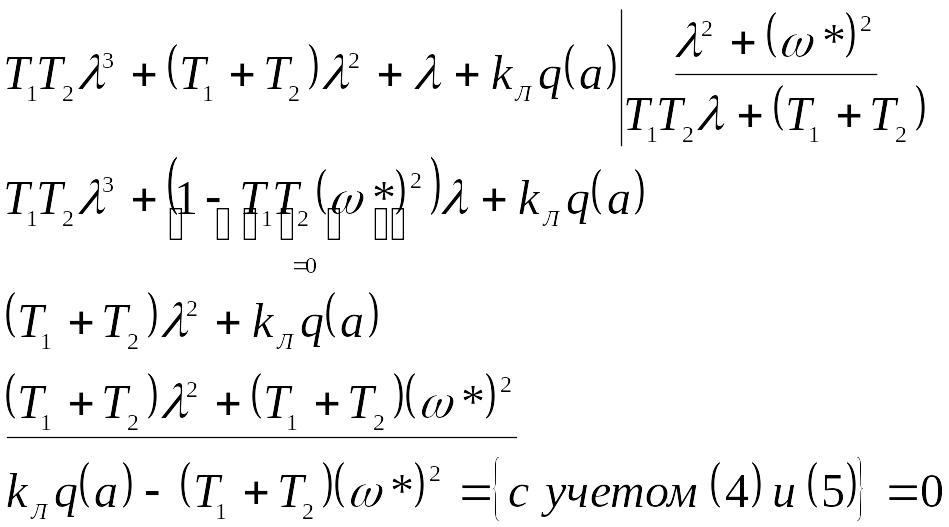Остаток от деления равен нулю (все верно!). Следовательно,

.

Корень последнего полинома

.

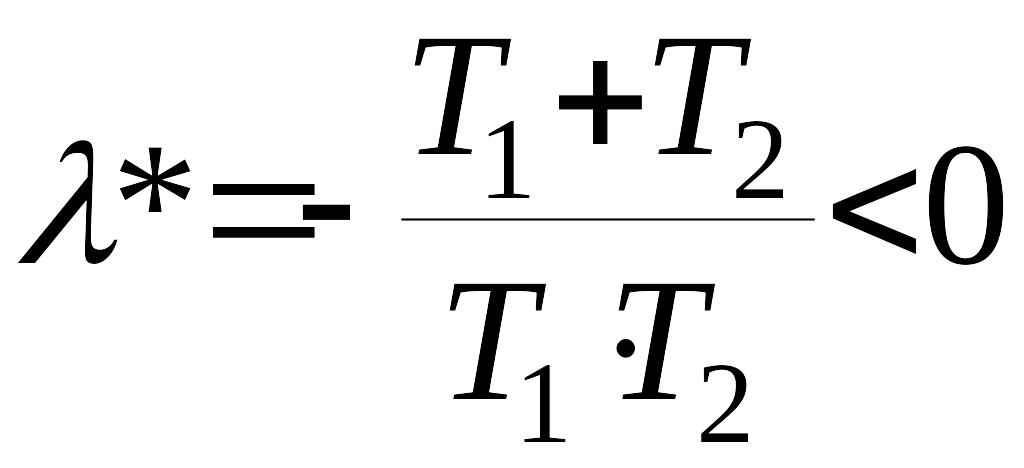Второе условие критерия устойчивости выполняется. Поэтому выполняется критерий устойчивости периодического решения.

Вывод. Периодическое решение с параметрами устойчиво, следовательно в системе есть автоколебания с амплитудой и частотой .

Практическое занятие 8. Применение метода гармонической линеаризации

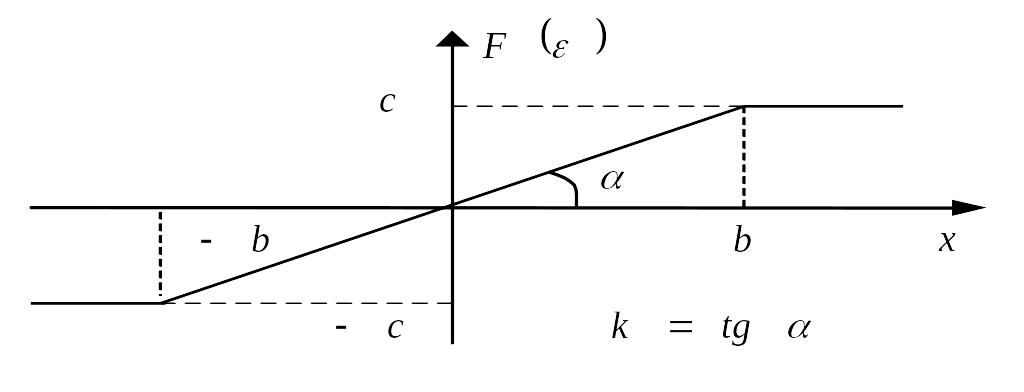
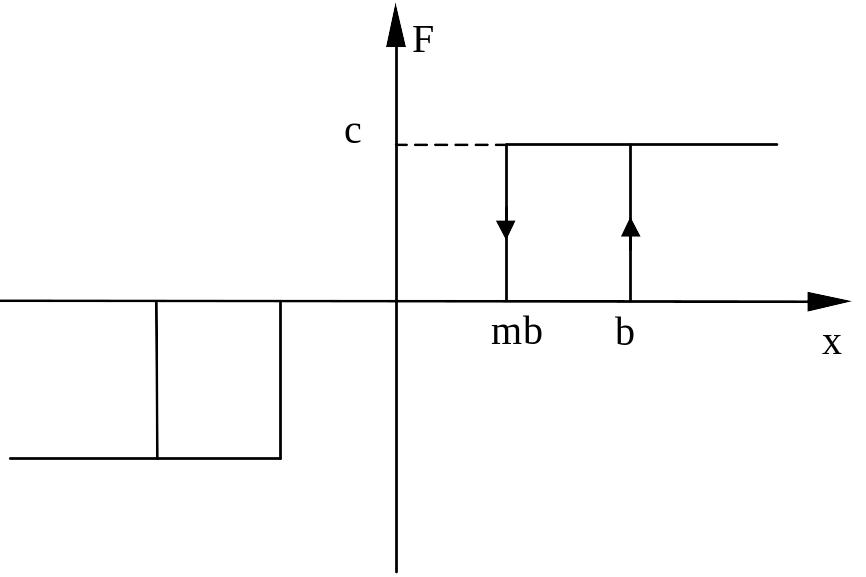
Пример. Выполнить гармоническую линеаризацию нелинейного звена системы автоматического управления, характеристика которого представлена на рисунке.

Решение. Имеем , , , .

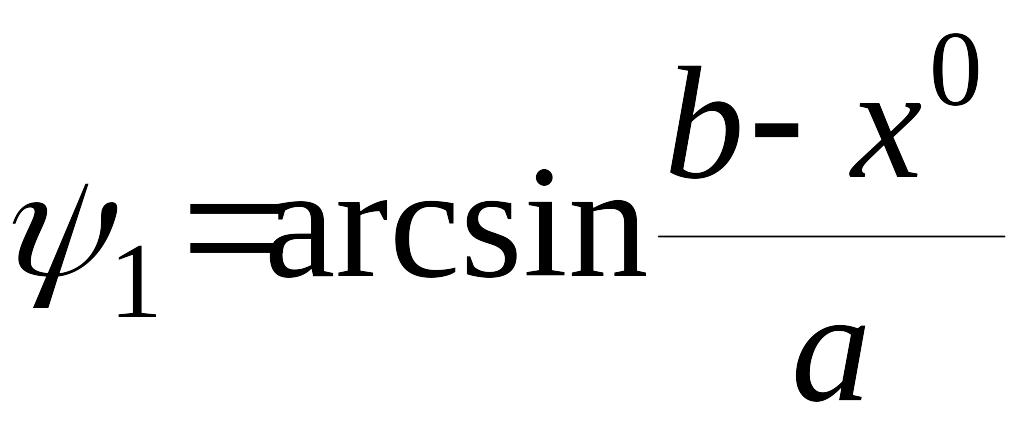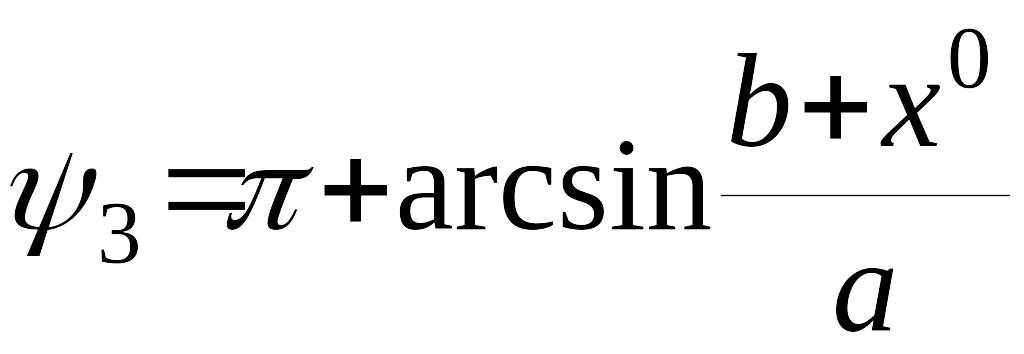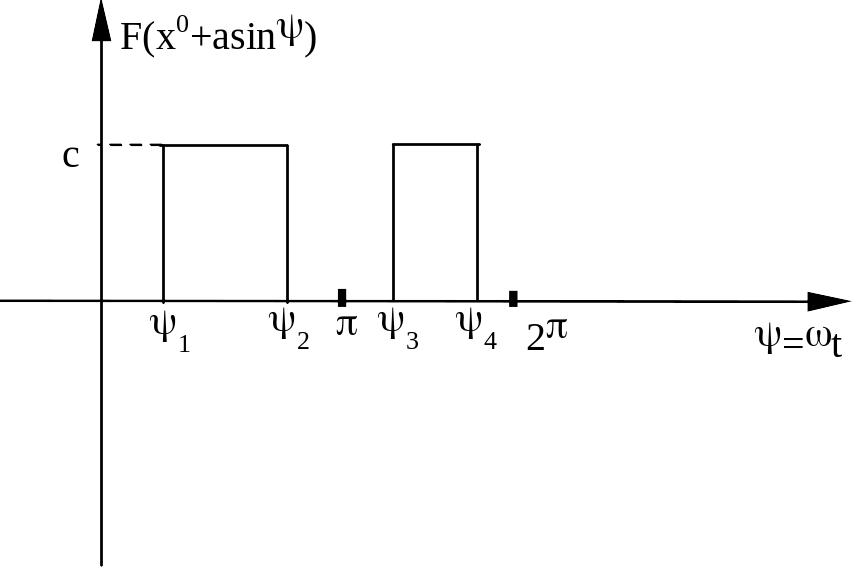
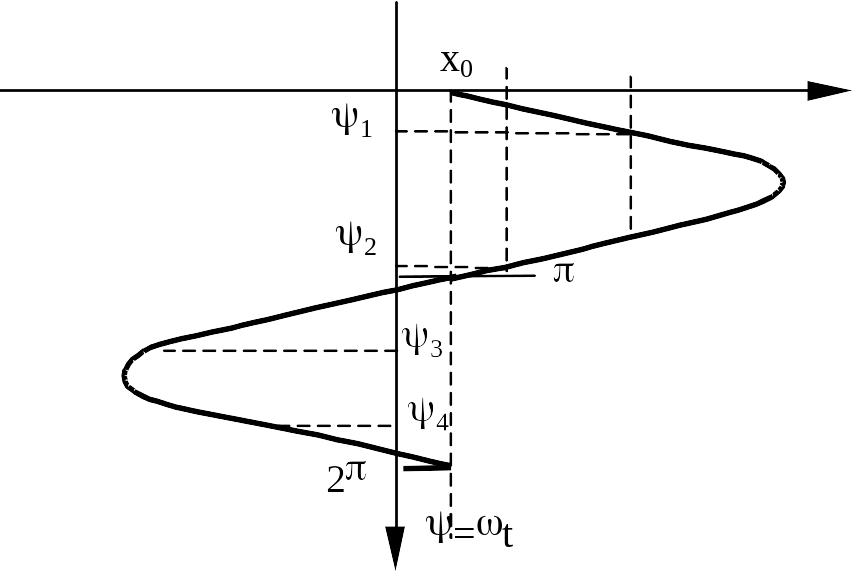
Далее получаем

,

,

.

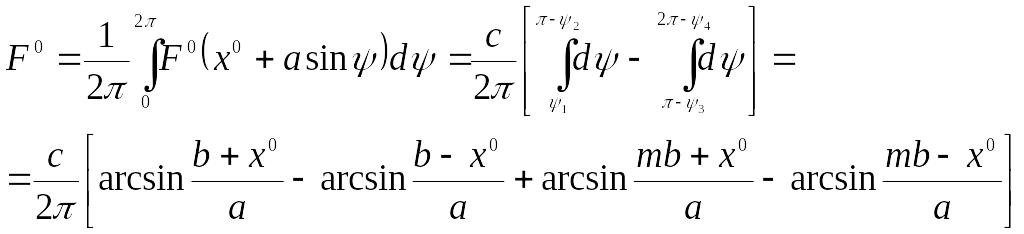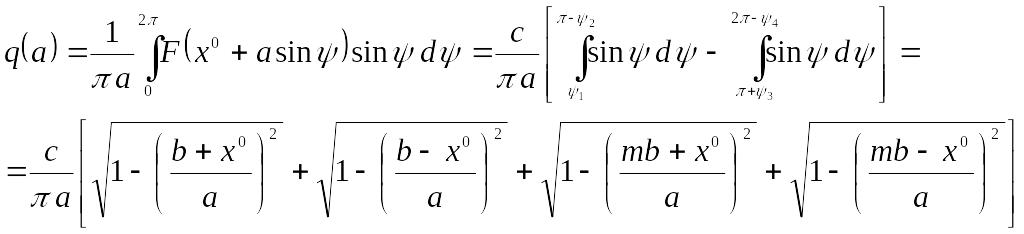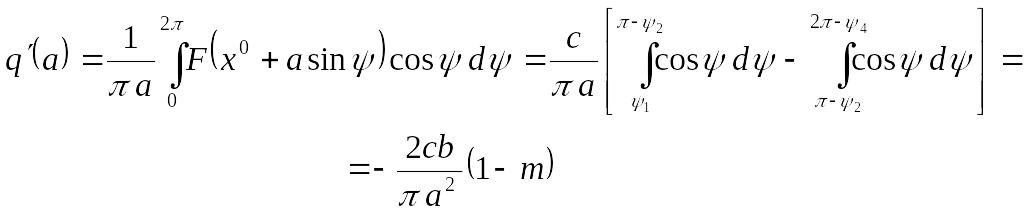Формулы справедливы при .

Практическое занятие 9. Гармоническая линеаризация нелинейности

Пример. Рассмотрим систему без внешнего воздействия, но при несимметричной нелинейности, структурная схема которой имеет вид

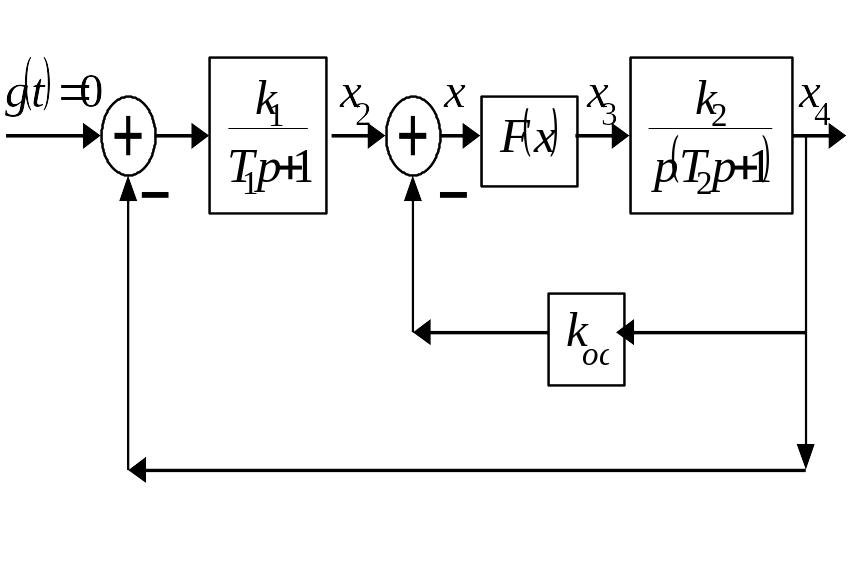
Нелинейное звено системы имеет следующую характеристику

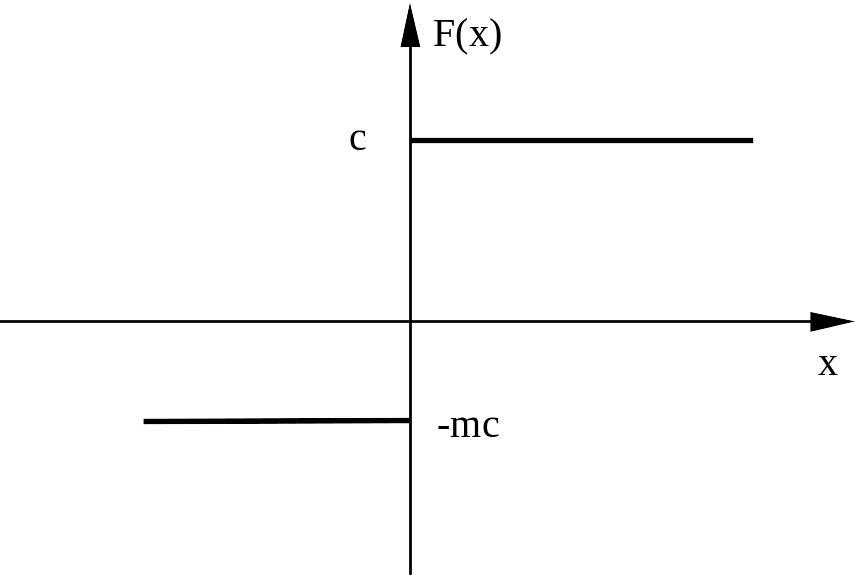
В соответствии с заданной структурной схемой динамика системы описывается следующими уравнениями

(*)

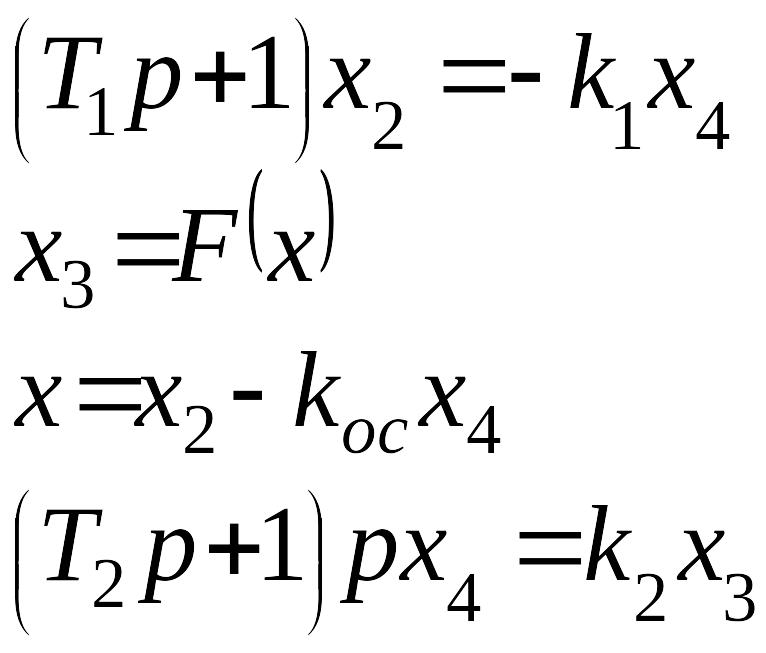Гармоническая линеаризация нелинейности:

, .

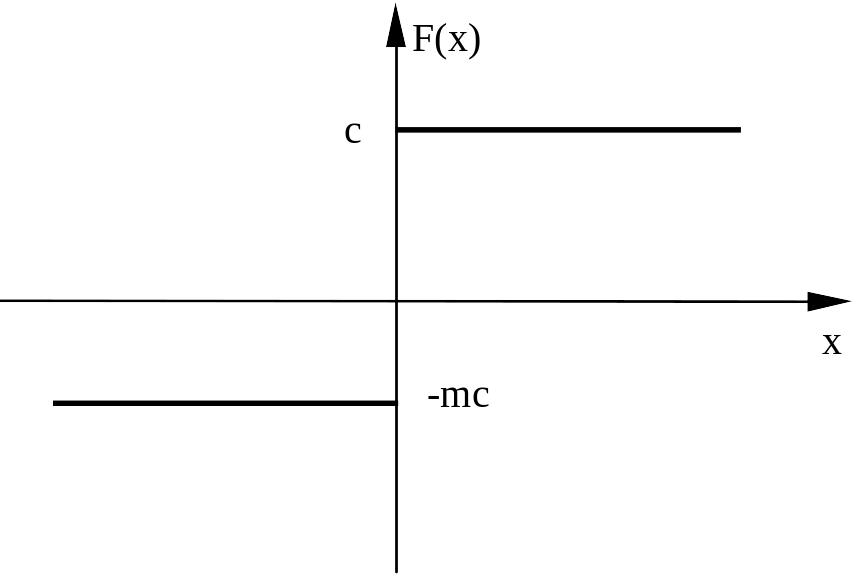
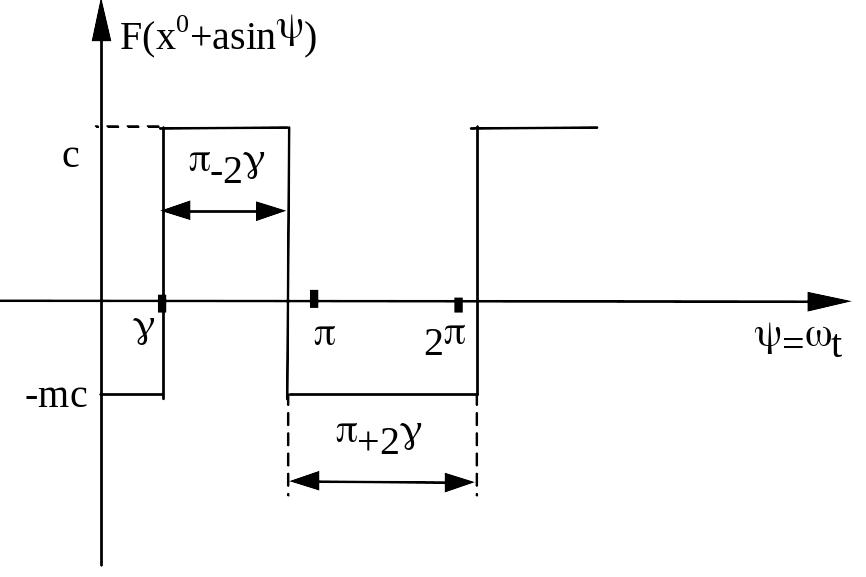
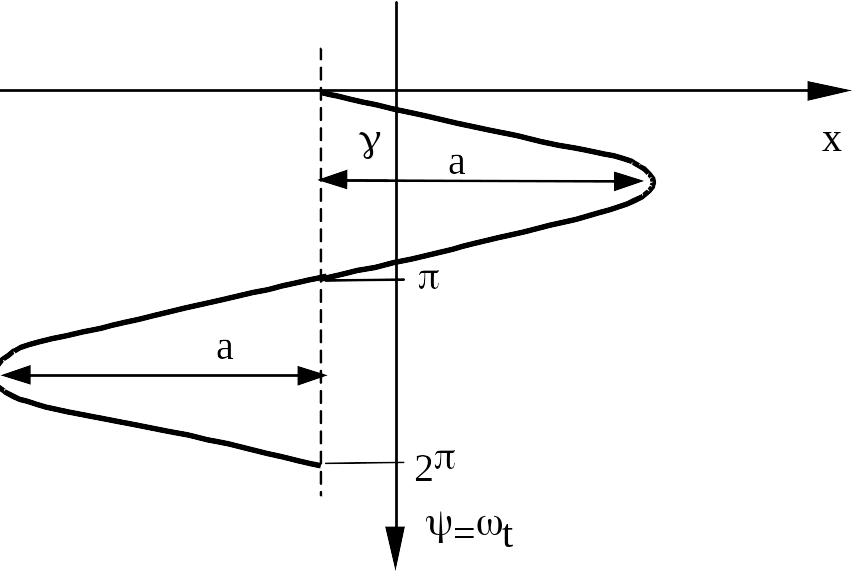
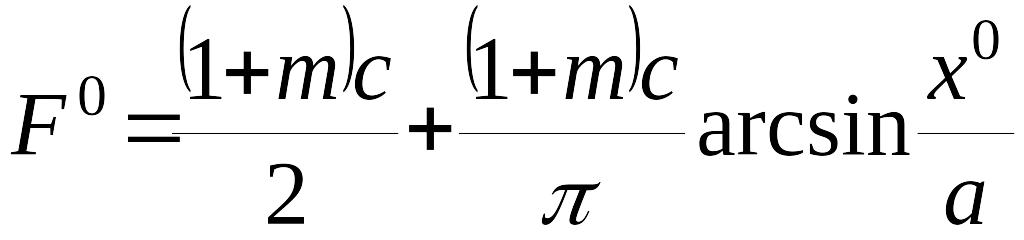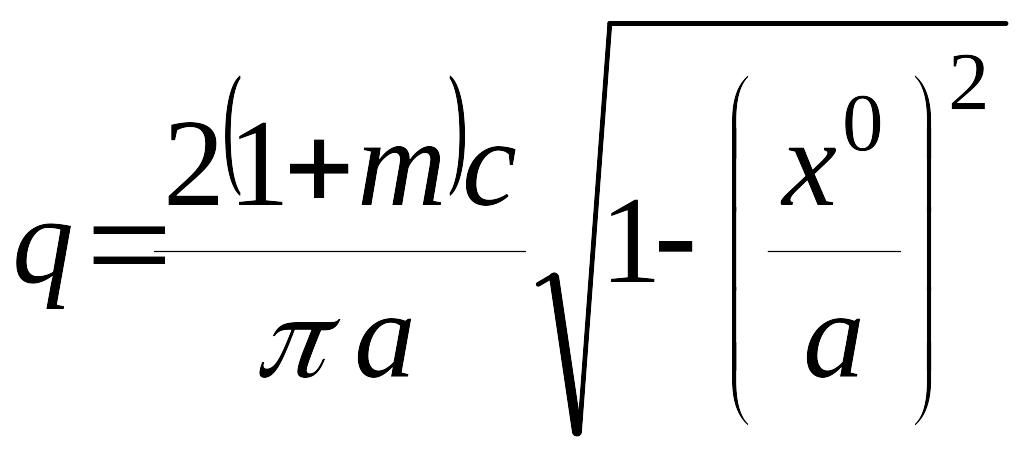Решение ищется в форме

.

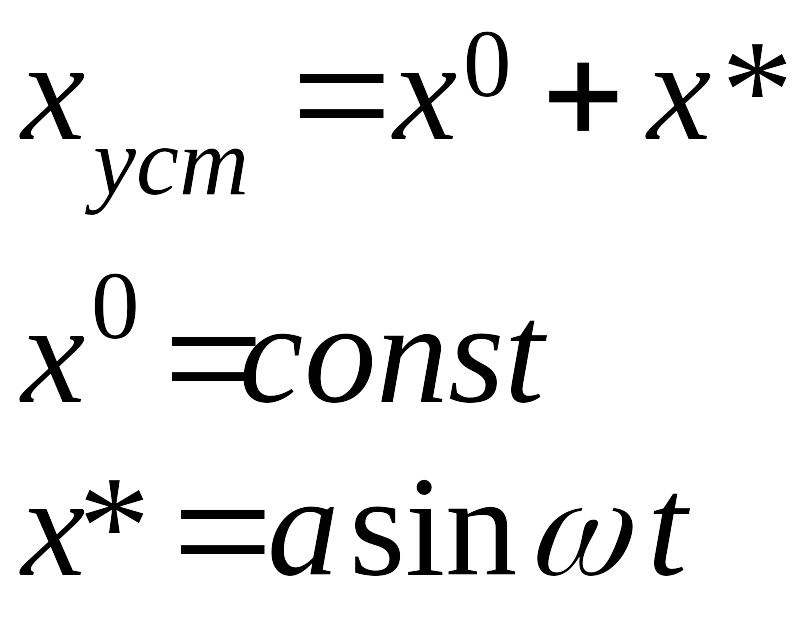Уравнение согласно системе (*) принимает вид или . Откуда находим

.

Подставив это в выражение для получаем

.

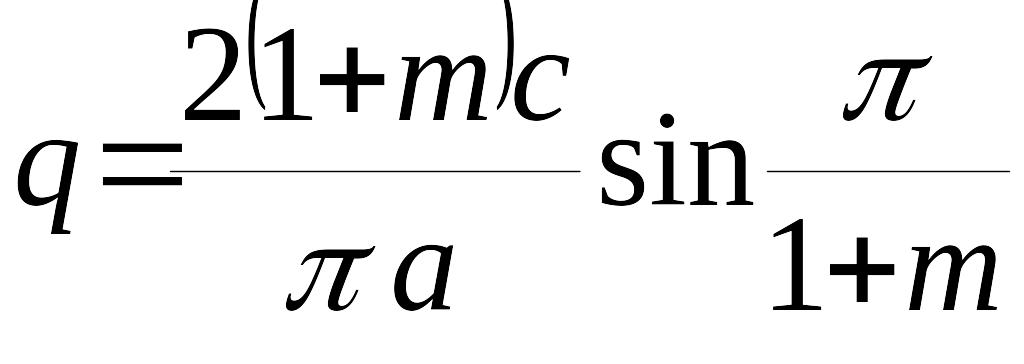Уравнение

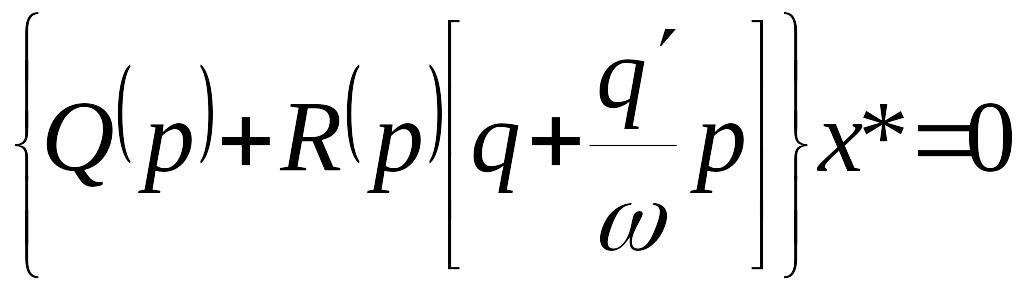
для данной системы будет иметь вид

.

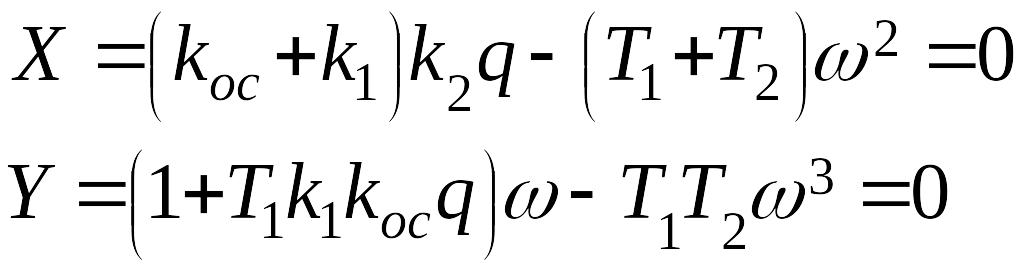С учетом этого получаем

,

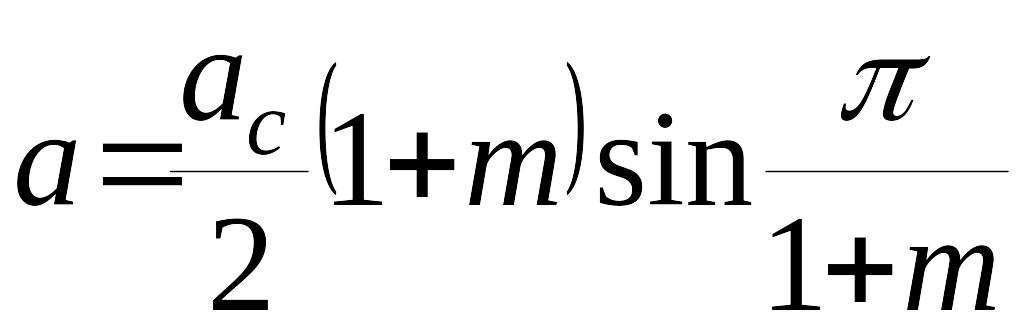где 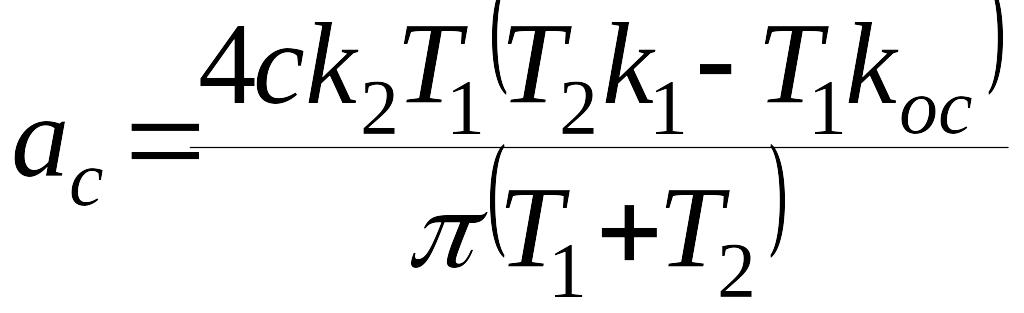– амплитуда автоколебаний в этой же системе, но для симметричной нелинейности. Частота автоколебаний

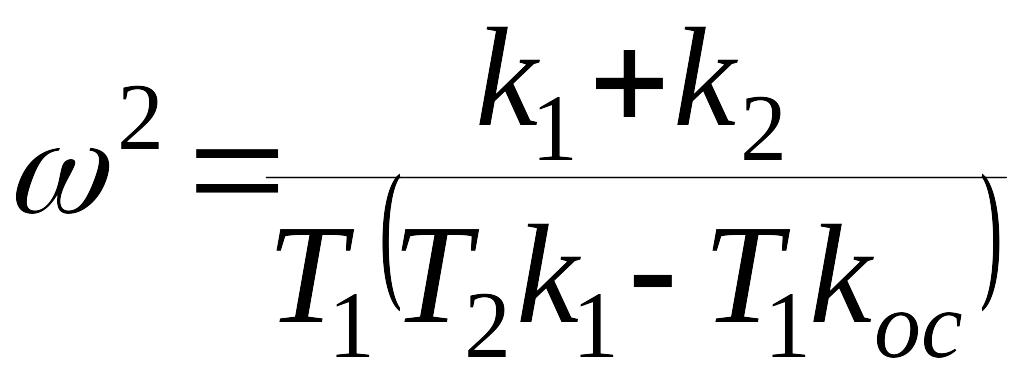
та же самая, что и в системе с симметричной нелинейностью.