Влияние параметров системы управления на тип особой точки. Бифуркация.

Рассматривается линейная система автоматического управления, собственное движение которой описывается линейными дифференциальными уравнениями

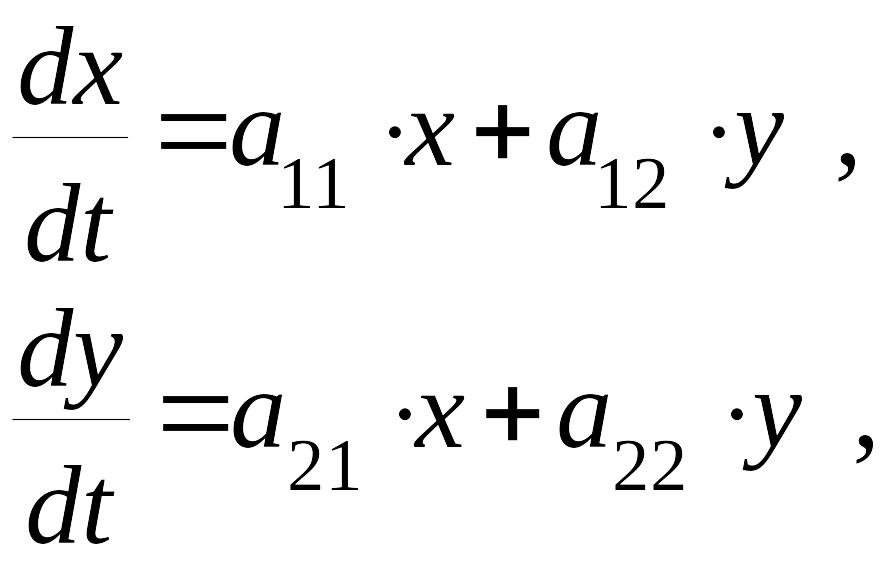
где ; начальные условия , считаются заданными.

Характеристическое уравнение системы

.

Координаты особой точки . В зависимости от корней характеристического уравнения определяется тип особой точки – характер собственных движений системы в окрестностях особой точки. В характеристическом уравнении системы

обозначим , . Тогда характеристическое уравнение перепишется следующим образом

.

Корни характеристического уравнения вычисляются согласно равенства

.

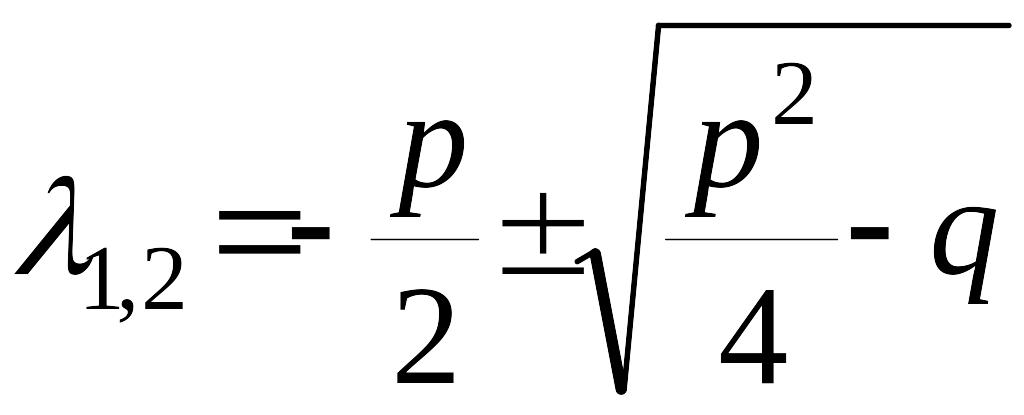В плоскости параметров системы и можно выделить области, занимаемые различными типами состояния равновесия (типами особых точек см. рисунок).

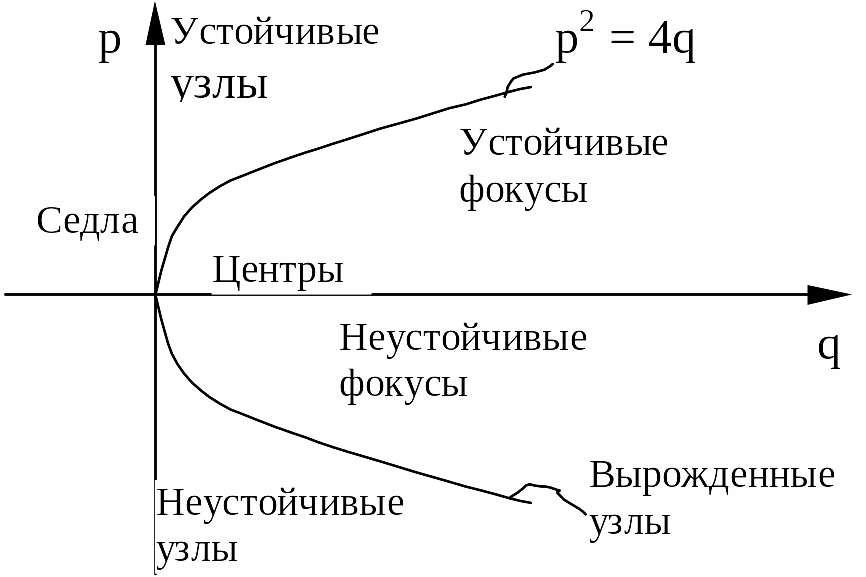
Парабола отделяет колебательные движения системы от апериодических (фокусы - узлы); – седла. Центры занимают пограничную линию между устойчивыми и неустойчивыми фокусами.

При изменении параметров системы качественные свойства особой точки (тип особой точки) изменяются.

Изменение типа особой точки системы при изменении значений ее параметров называется БИФУРАКЦИЕЙ.

Из рисунка видно, как может меняться тип особой точки при изменении значения того или иного параметра системы ; : неустойчивый фокус  центр  устойчивый фокус  устойчивый узел.

Практическое занятие 3. Построение фазового портрета нелинейной системы.

Пример. Установить типы особых точек нелинейной системы

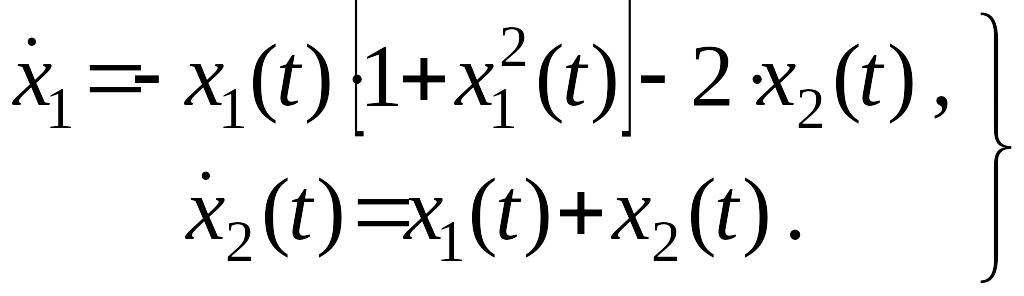
Построить фазовый портрет.

Решение. Определим координаты особых точек

, ,

, ,

, , .

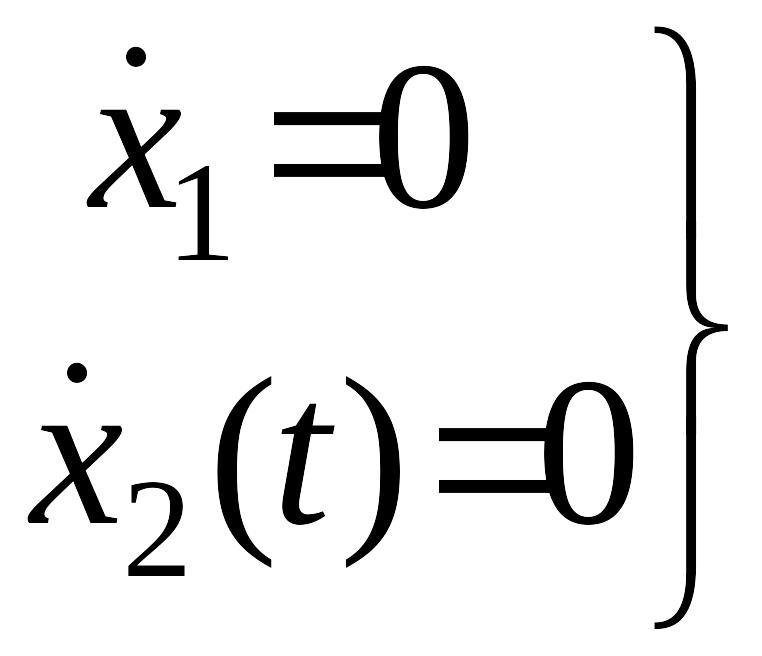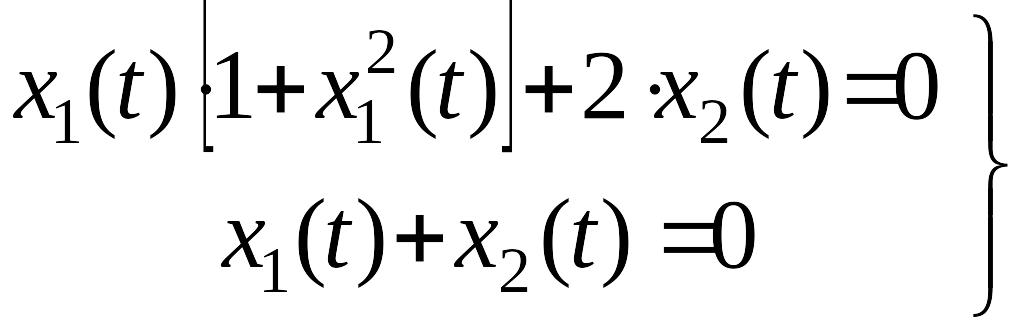Координаты особых точек:

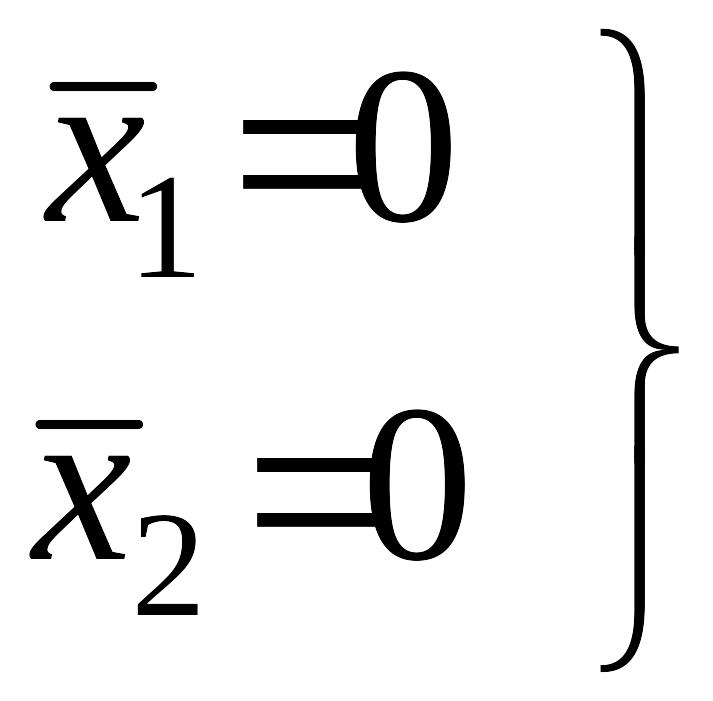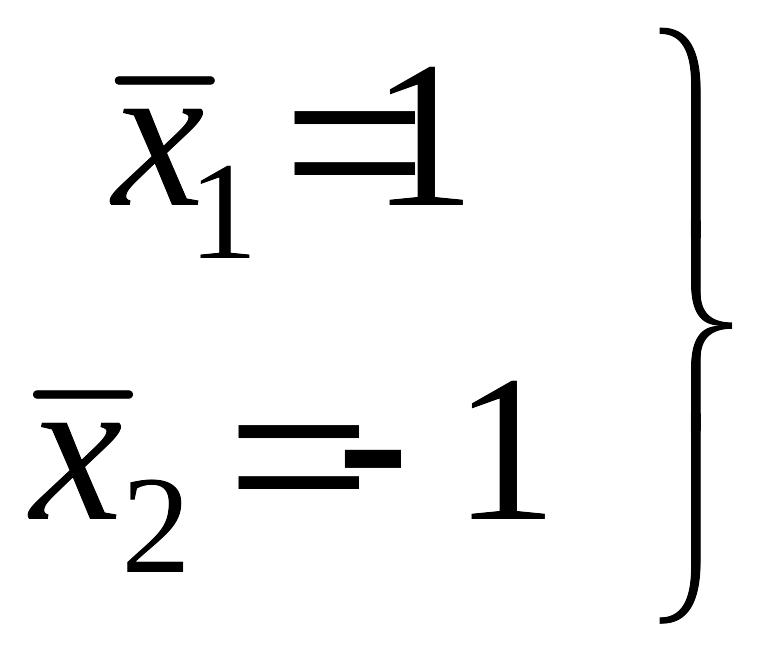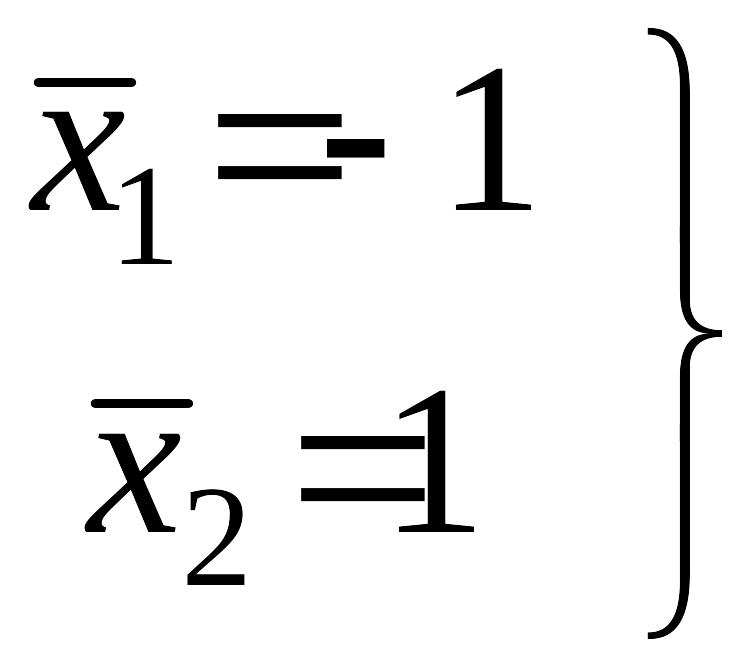(I) , (II) , (III)

Исследуем типы особых точек:

(I) особая точка , ее координаты .

В окрестности этой особой точки является бесконечно малой более высокого порядка малости чем переменные и . Поэтому уравнения системы первого приближения (уравнения в отклонениях) будут иметь вид

.

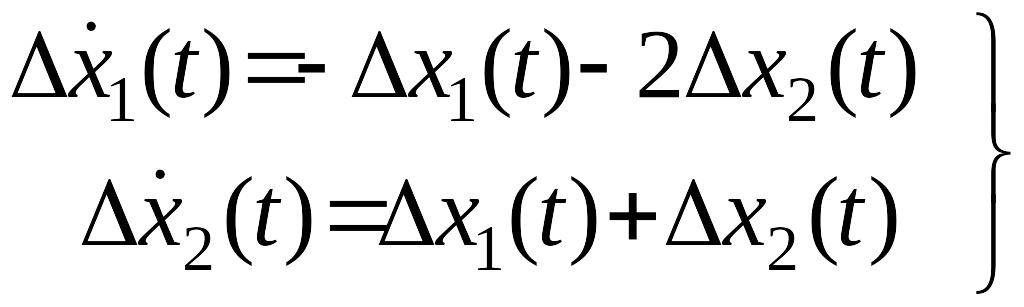Это линейная система дифференциальных уравнений относительно и . Определим тип этой особой точки. Характеристическое уравнение

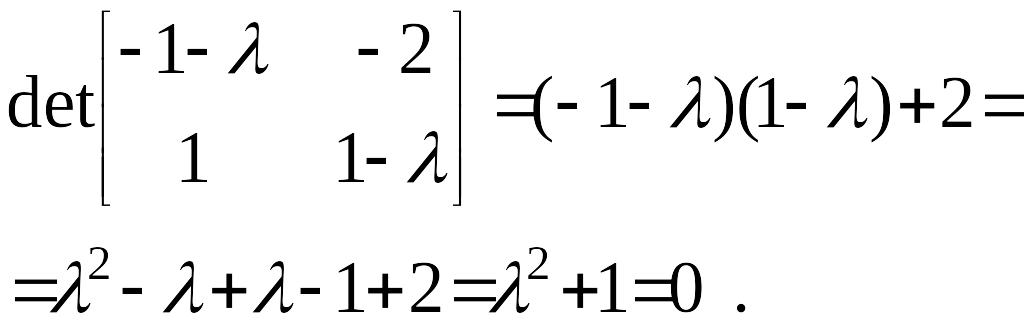
– корни характеристического уравнения чисто мнимые, следовательно, особая точка типа ЦЕНТР.

(II) особая точка, ее координаты .

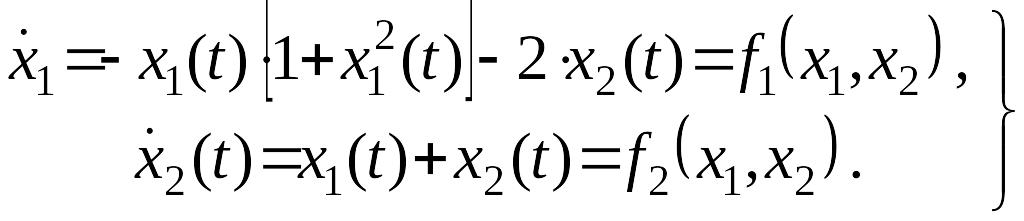
Составим уравнение в отклонениях:

,

, , .

.

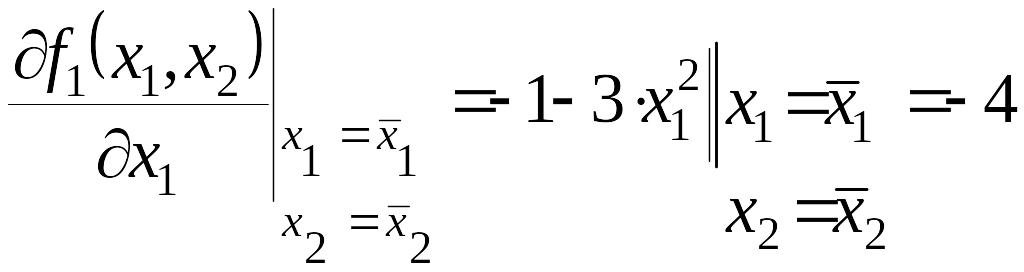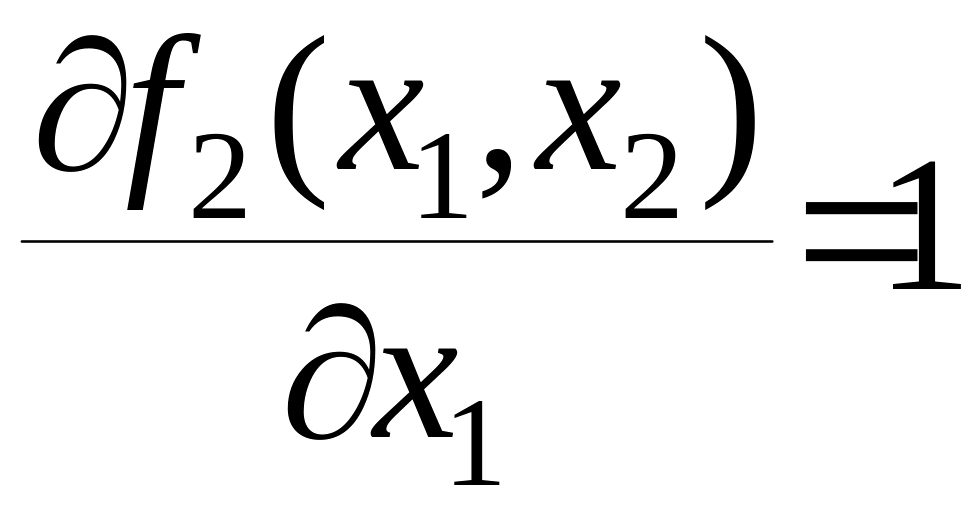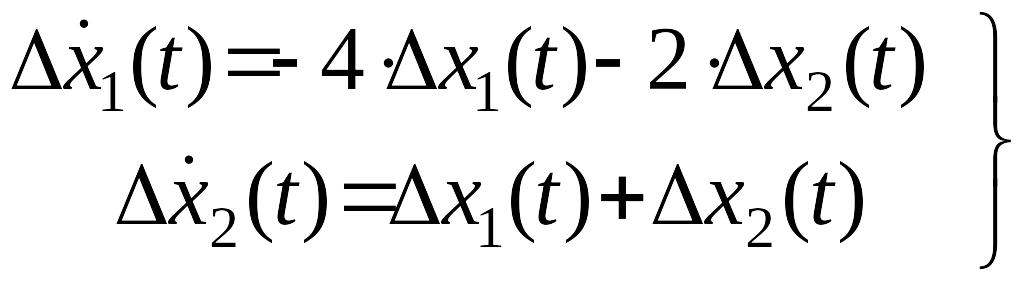Определим тип этой особой точки. Характеристическое уравнение

,

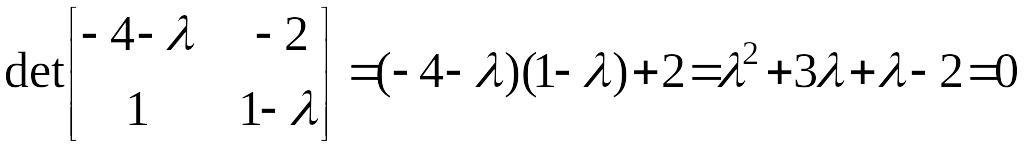корни характеристического уравнения

.

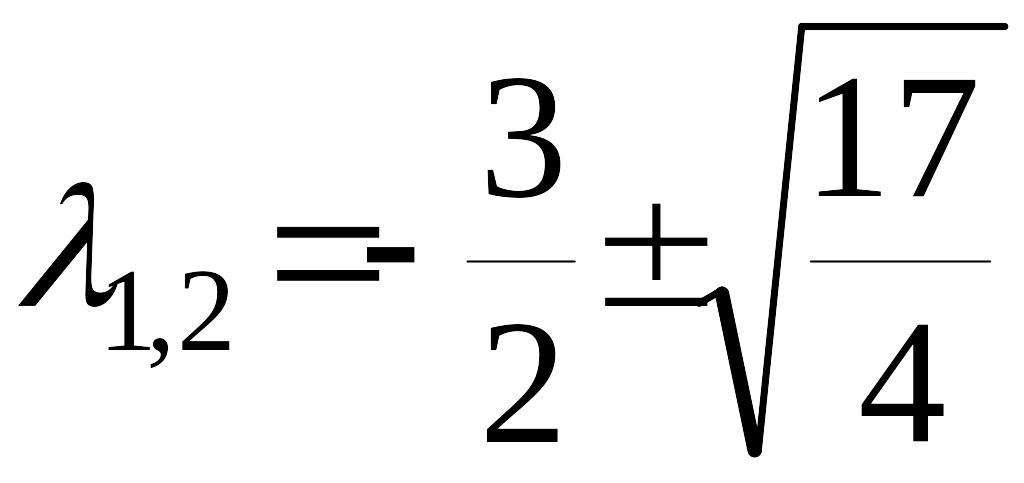Корни характеристического уравнения действительные различного знака; особая точка СЕДЛО.

(III) особая точка ее координаты .

Другой способ определения уравнений первого приближения: перенос начала координат: , ,

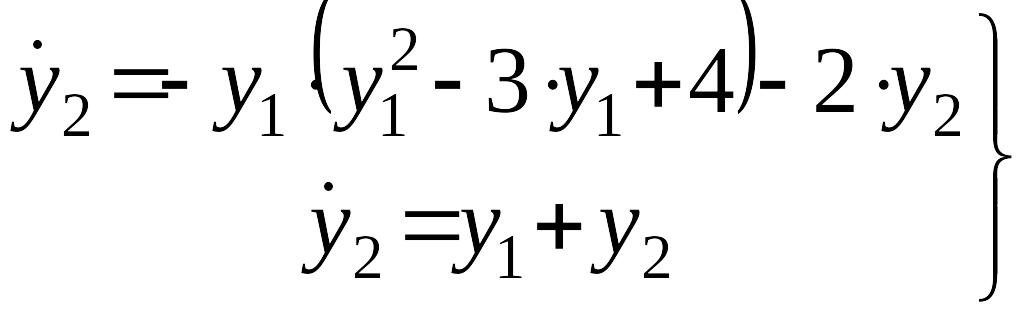
Теперь в новых координатах особая точка .Аналогично первой особой точке является в окрестности бесконечно малой более высокого порядка, чем и .Тогда уравнения первого приближения принимают вид

.

Определим тип этой особой точки. Характеристическое уравнение

,

корни характеристического уравнения

,

следовательно, особая точка – СЕДЛО.

Оси эллипсов в окрестности особой точки (I). Дифференциальные уравнения системы в окрестности этой особой точки

,

дифференциальное уравнение фазовых траекторий

,

, ,

,

,

, , .

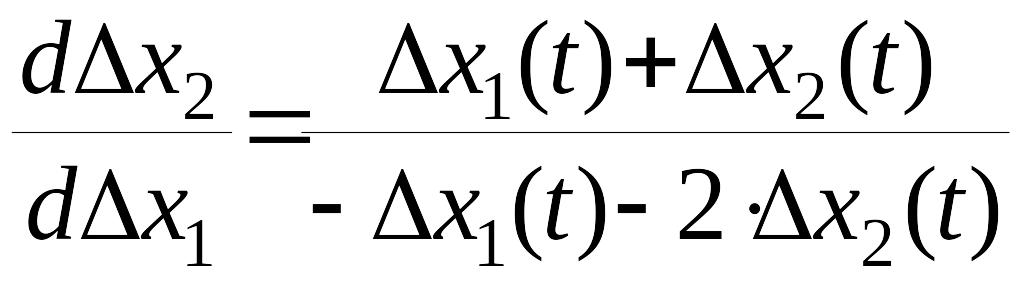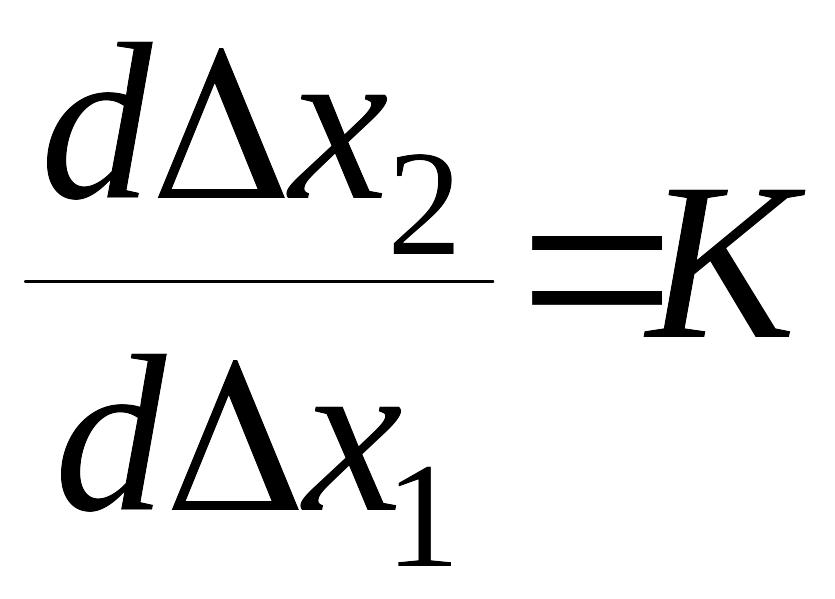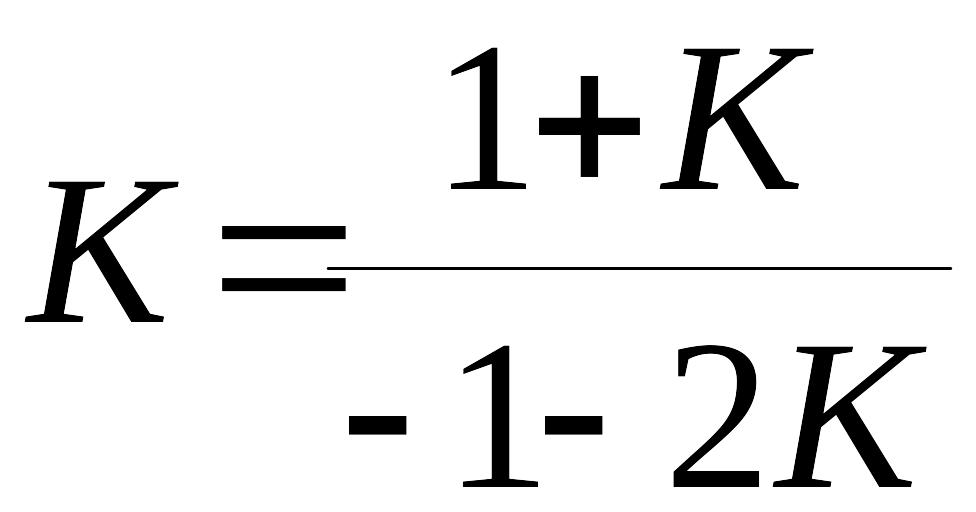Прямая ось эллипса.

Асимптоты в особой точке (II).

,

Дифференциальное уравнение фазовых траекторий

,

, ,

, ,

, ,

,

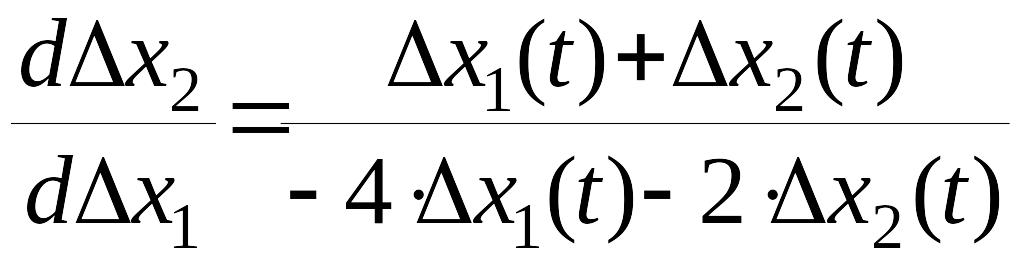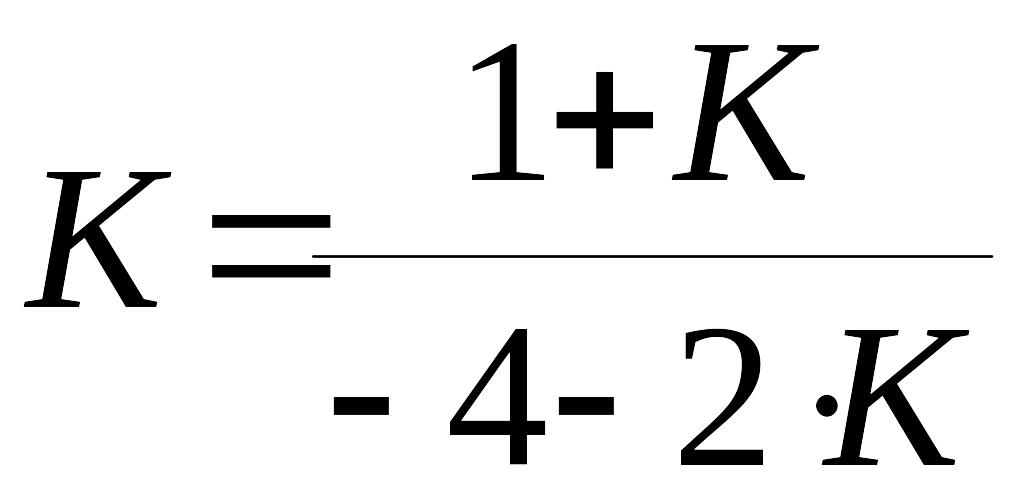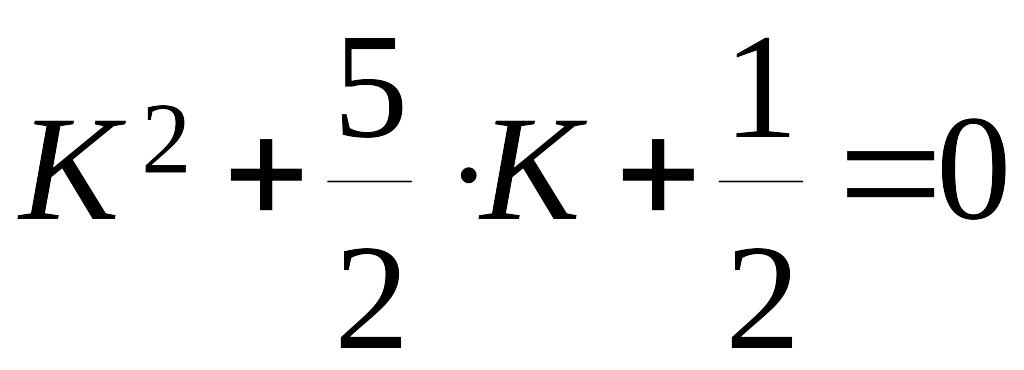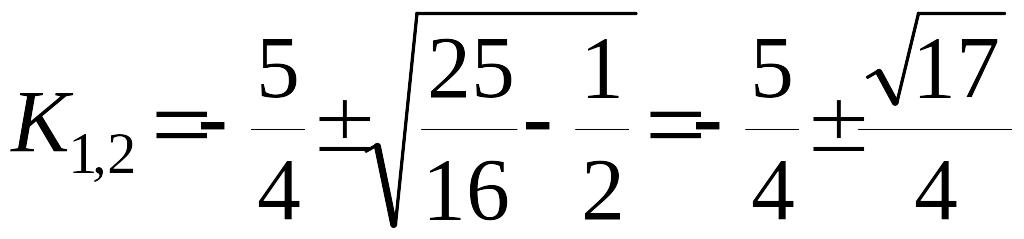Асимптоты в окрестностях особой точки (III).

, , .

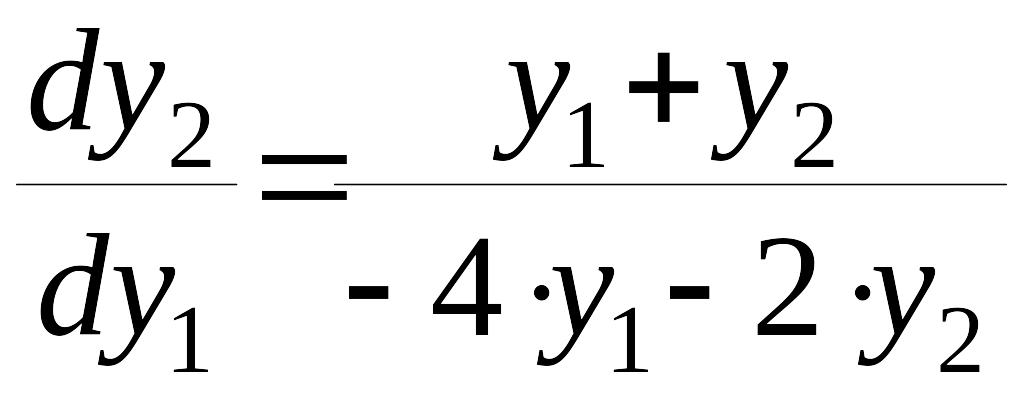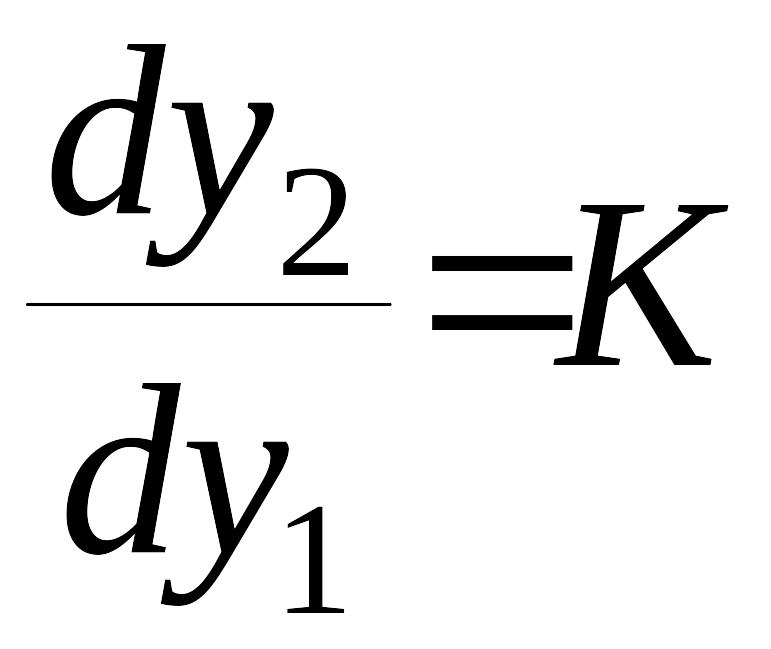Асимптоты в особых точках (II) и (III) совпадают совпадают тангенсы углов наклона этих асимптот.

Для определения движения изображающей точки по фазовым траекториям найдем компоненты вектора фазовой скорости в точке пересечения асимптоты, проходящую через точку с угловым коэффициентом

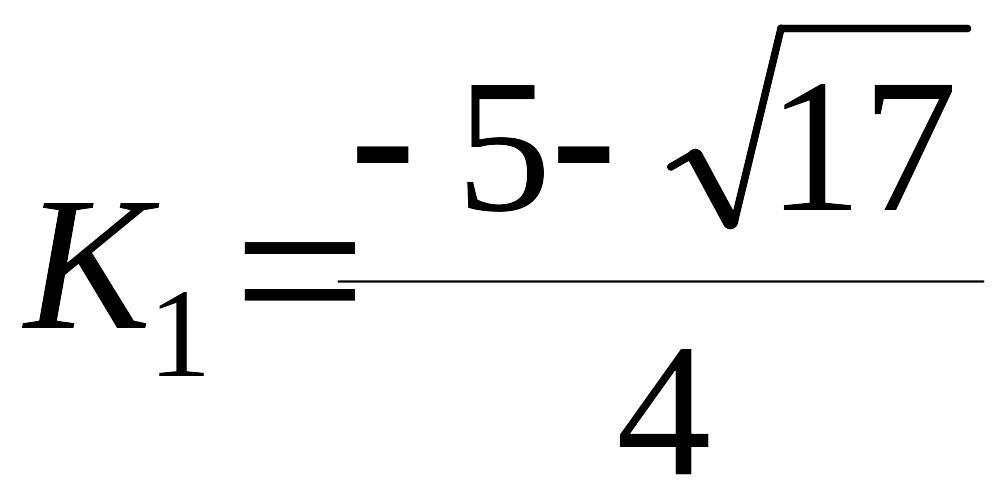
и осью ; уравнение асимптоты

,

координаты точки :

, ,

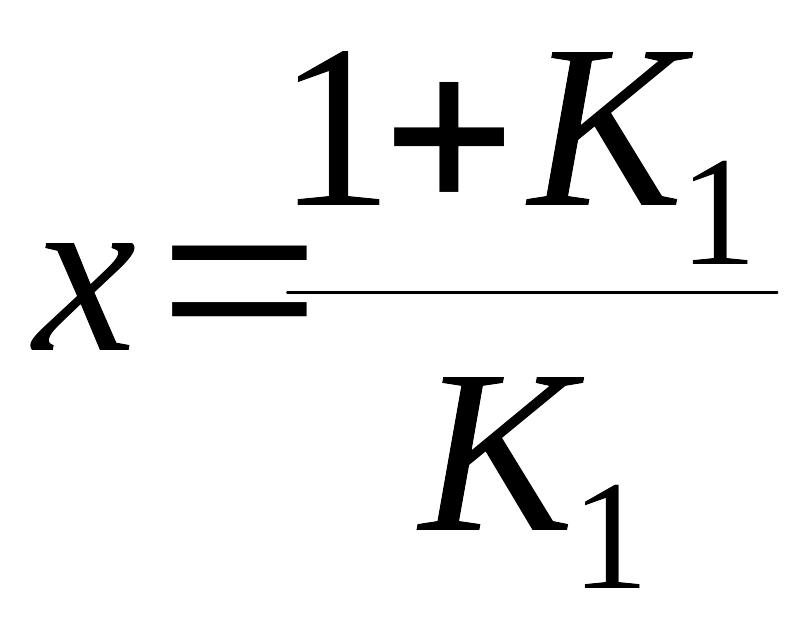компоненты вектора скорости в точке :

, .

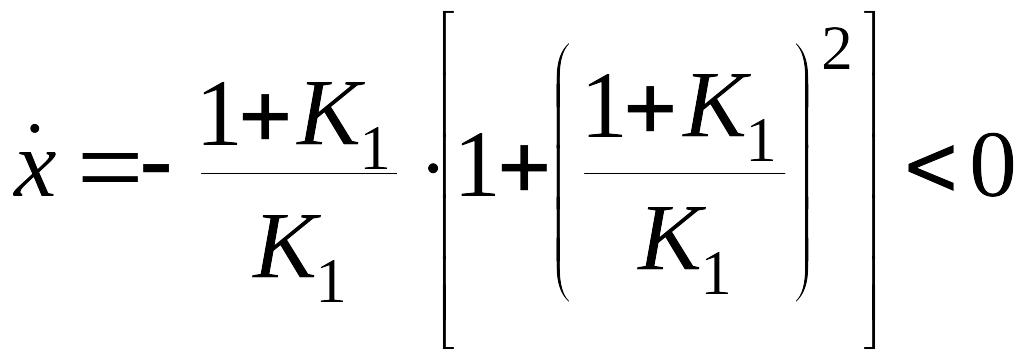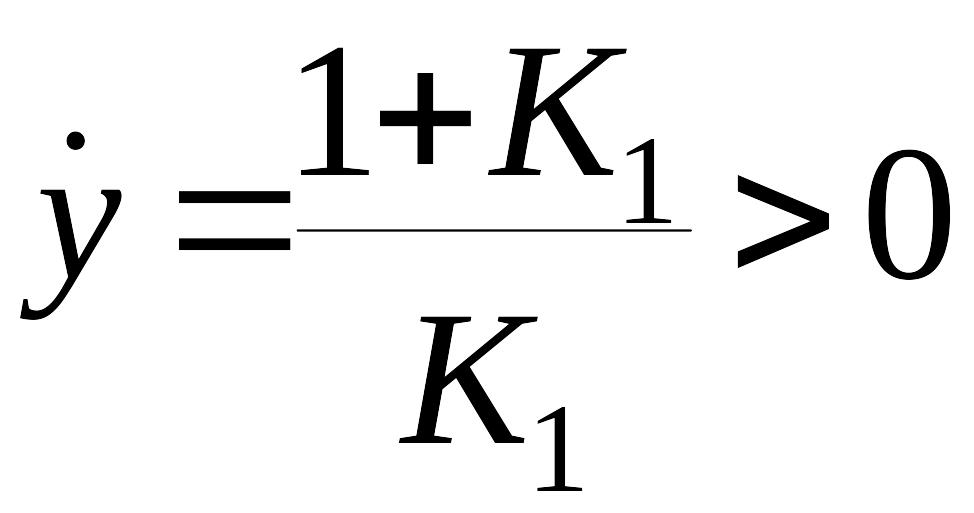Фазовый портрет системы

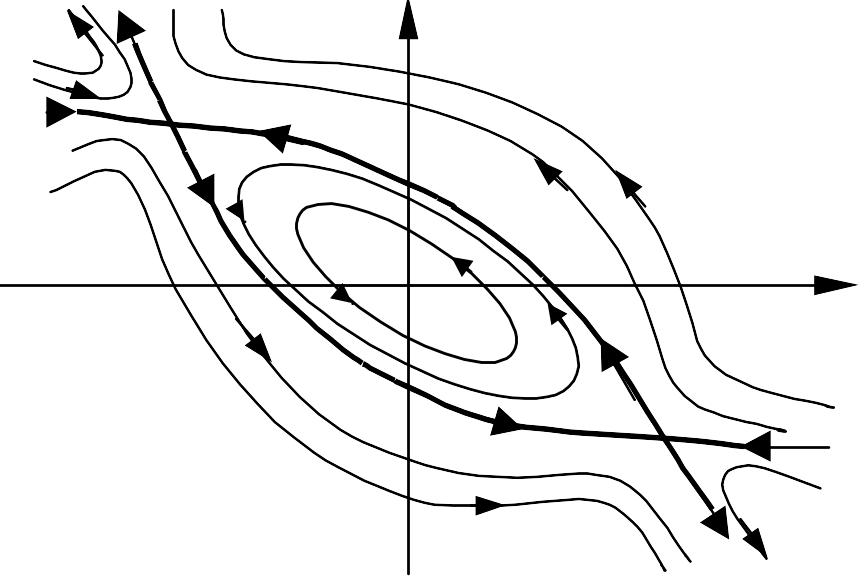
Практическое занятие 4. Качественный анализ систем управления

Задача. Провести качественный анализ процессов в системе управления методом фазовой плоскости при . Исследуем собственные движения системы.

РЕШЕНИЕ. Согласно заданной структурной схеме математической моделью процессов в исследуемой системе являются следующие уравнения

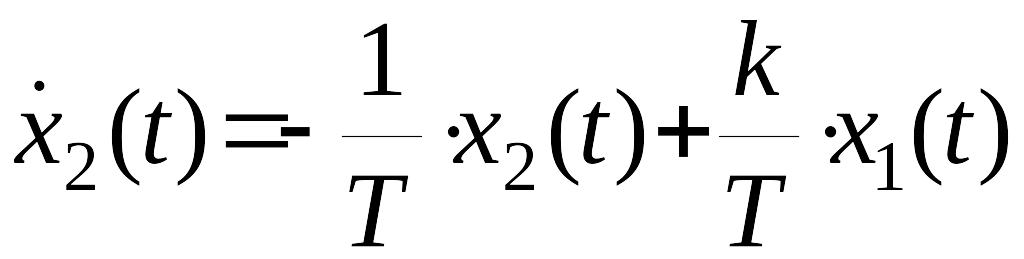, (1)

, (2)

Уравнение (2) записано с учетом свойства нечетности заданной релейной характеристики.

Для того, чтобы упростить аналитические выкладки, выполним преобразование исходной математической модели (1) (2) системы управления. Продифференцируем уравнение (1), а затем подставим в него уравнение (2). В результате получаем

, (3)

Уравнение (3) запишем относительно переменных состояния в следующем виде

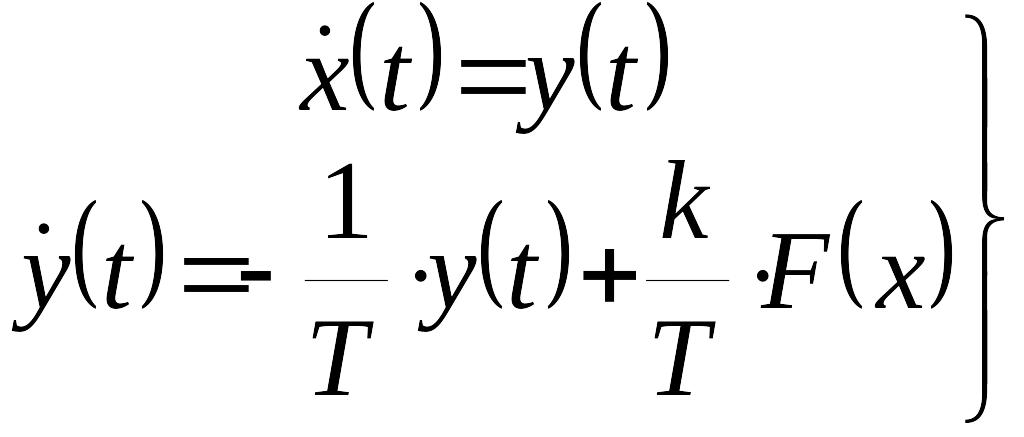. (4)

Здесь обозначено – выходная переменная системы – скорость изменения выходной переменной системы. Из полученной системы уравнений (4) получим дифференциальное уравнение фазовых траекторий, поделив второе уравнение системы (4) на первое

. (5)

Как следует из заданной характеристики нелинейного звена, нелинейное звено с характеристикой можно представить в виде следующей математической модели.

Если , то

,

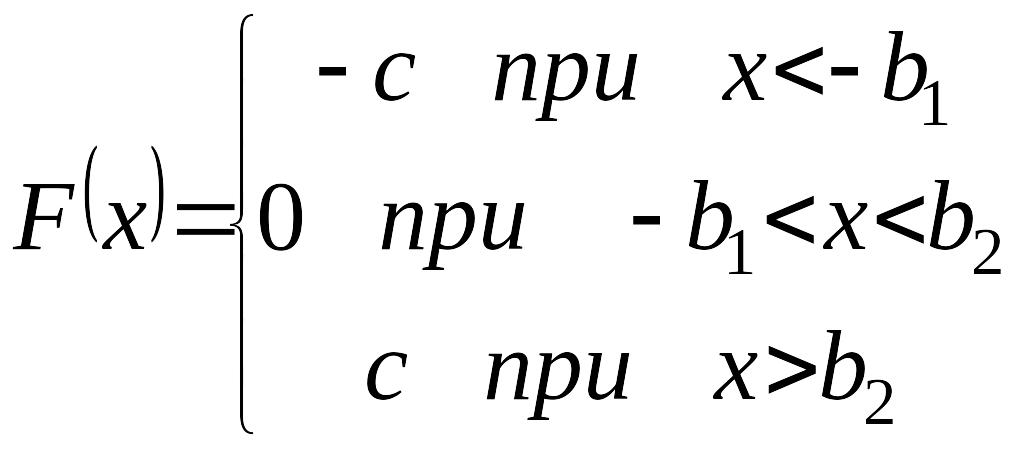если , то

.

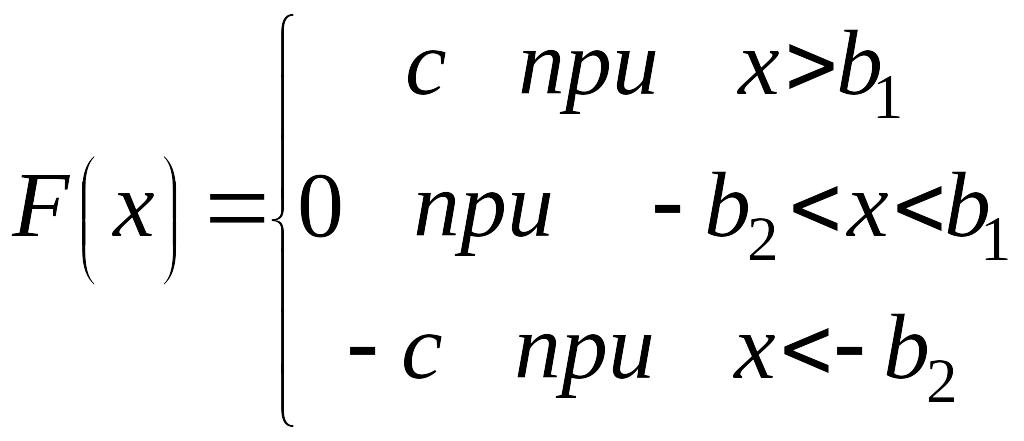В связи с этим на фазовой плоскости можно выделить три области: область I, где , область II, где и область III, где .

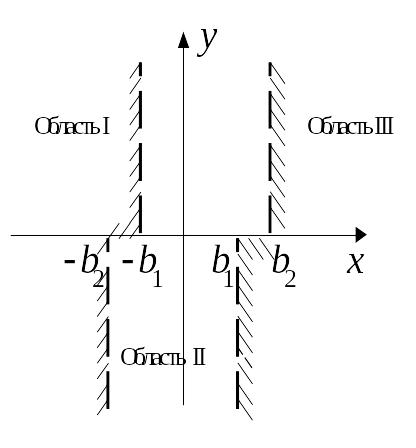
Линии, разделяющие фазовую плоскость на различные области – линии переключения (пунктирные линии на рисунке). Такую фазовую плоскость часто называют многолистной. На каждом листе (области I, II,III,) получаем свой вид фазовых траекторий. По линиям переключения эти листы (области) «сшиваются». Фазовые траектории переходят из одной области (с одного листа) на другой последовательно пересекая линии переключения, на которых меняется скачком значение , за исключением особых случаев, когда фазовые траектории встречаются.

Получим уравнение для фазовых траекторий в каждой из данных областей.

ОБЛАСТЬ I. В этой области и, следовательно, дифференциальное уравнение фазовых траекторий принимает вид

. (6)

Уравнение (6) является линейным дифференциальным уравнением с разделяющимися переменными. Решим его

, ,

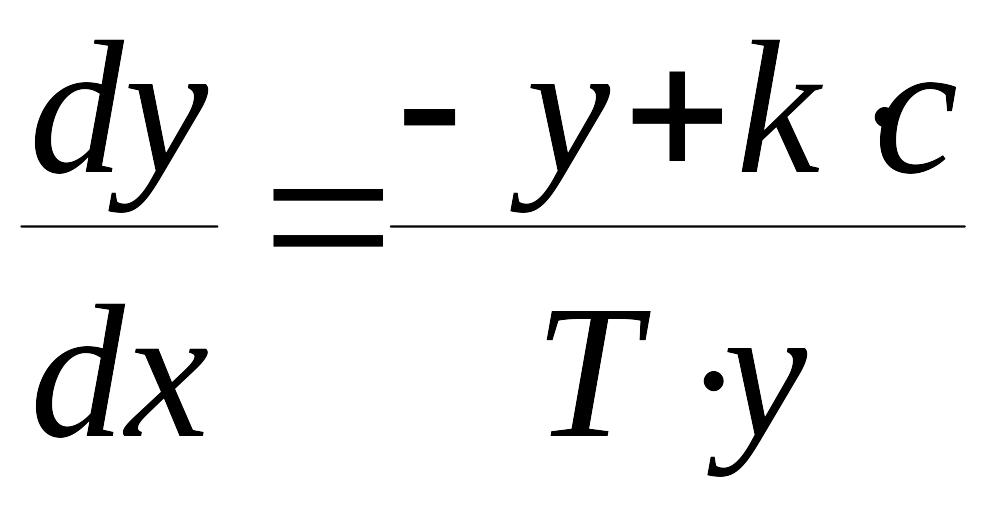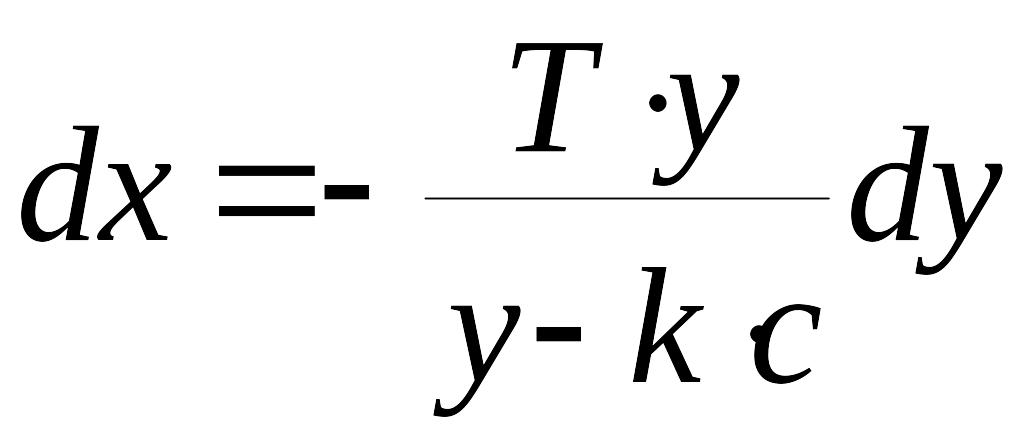, (6.1)

Вычислим интеграл, стоящий в правой части равенства (6.1)

.

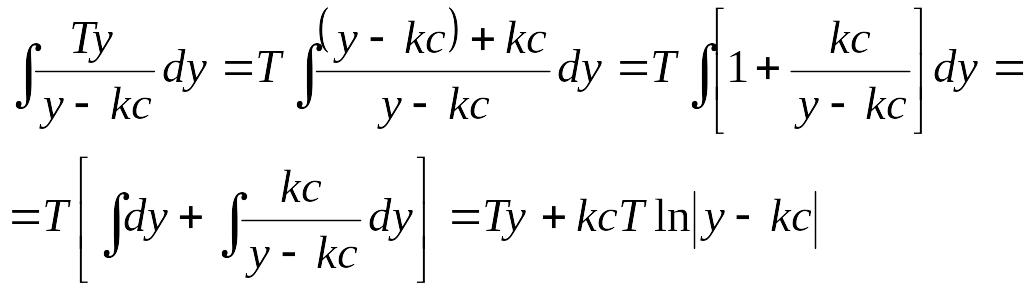Таким образом, интегрирование уравнения (6) в области I дает следующий результат

, (7)

где – постоянная интегрирования, которая определяется начальными условиями. Уравнение (7) – это уравнение фазовых траекторий системы в области (I). Из уравнения (7) следует, что фазовые траектории имеют асимптоту

. (8)

Движение изображающей точки по фазовым траекториям, где происходит слева направо; в нижней полуплоскости, где – справа налево. На рисунке изображены фазовые траектории системы для области I. Напомним, что для этой области .

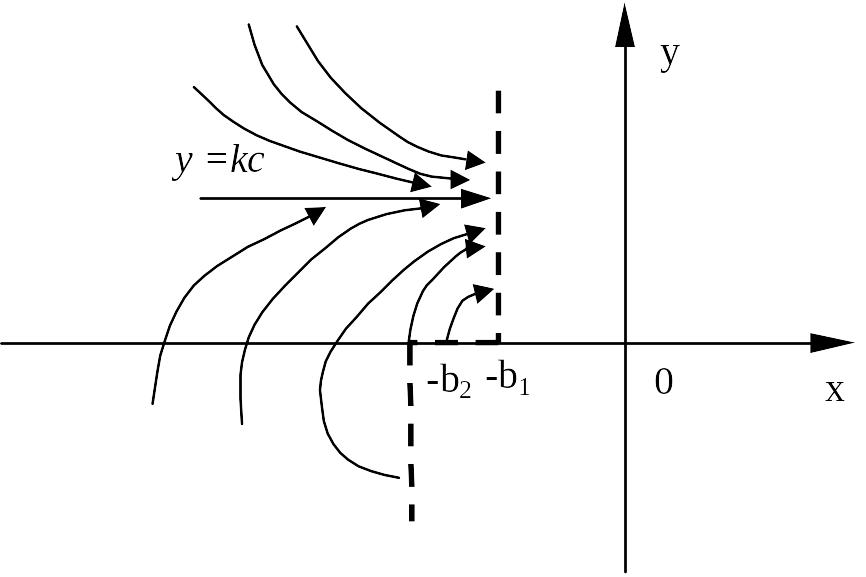
ОБЛАСТЬ II. В области II значение и равенство (6) принимает вид

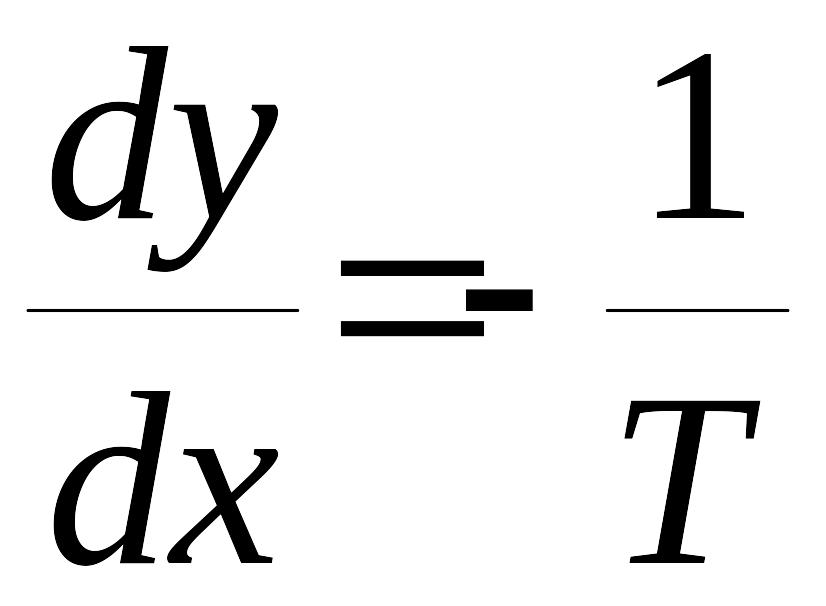. (9)

Уравнение (9) – это дифференциальное уравнение фазовых траекторий в этой области. Проинтегрировав его получим уравнение фазовых траекторий

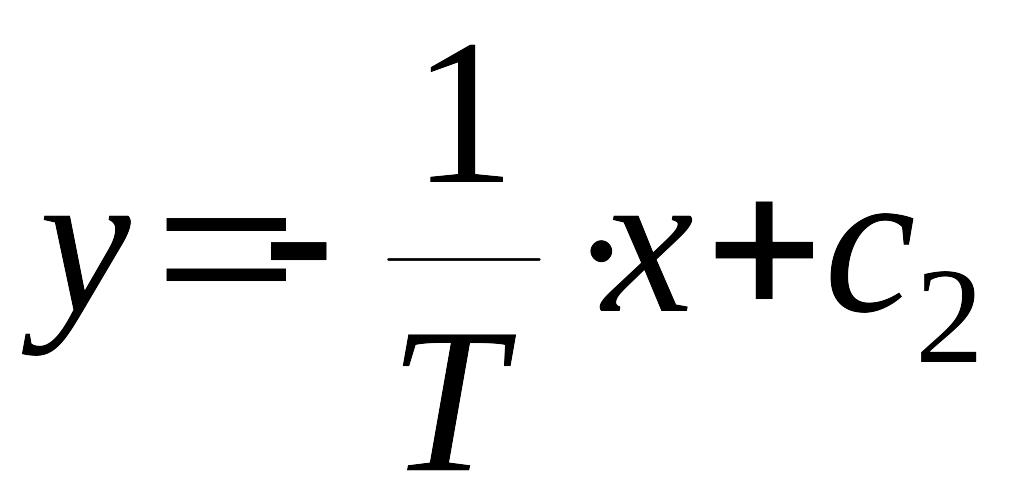. (10)

Из уравнения (10) следует, что во второй области фазовые траектории – это прямые. В верхней полуплоскости движение изображающей точки будет происходить слева направо так как . В нижней полуплоскости движение изображающей точки будет происходить справа налево так как .

На рисунке изображены фазовые траектории системы для области II. Напомним, что для этой области .

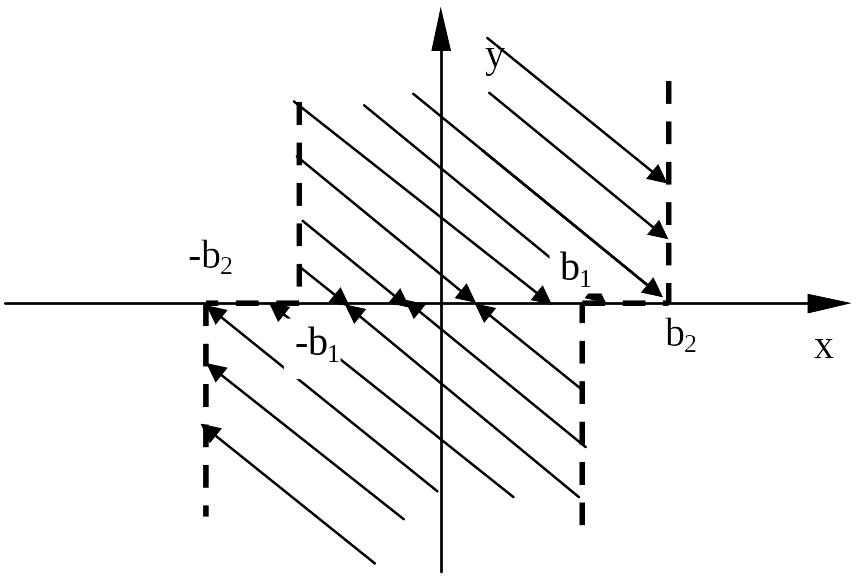
ОБЛАСТЬ III. В этой области и уравнение (5) принимает вид

. (11)

Уравнение (11) – линейное дифференциальное уравнение с разделяющимися переменными. Найдем решение дифференциального уравнения (11).

,

, ,

,

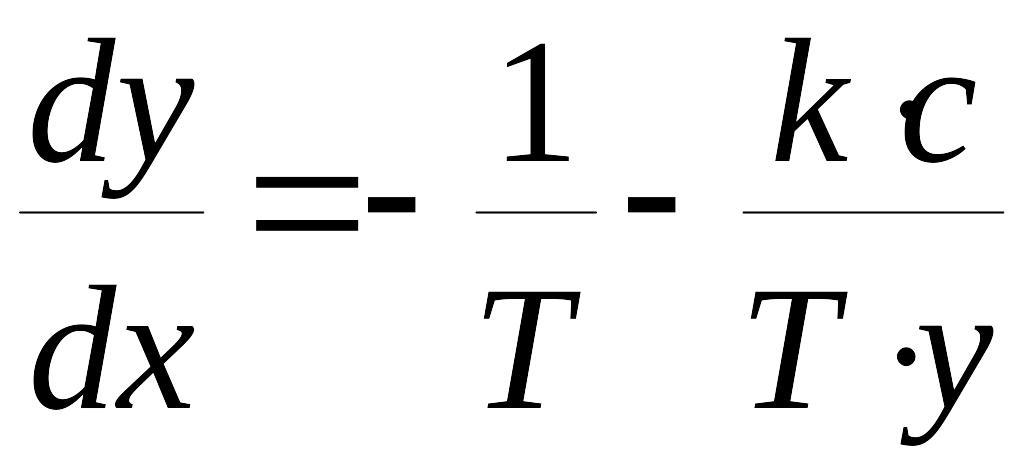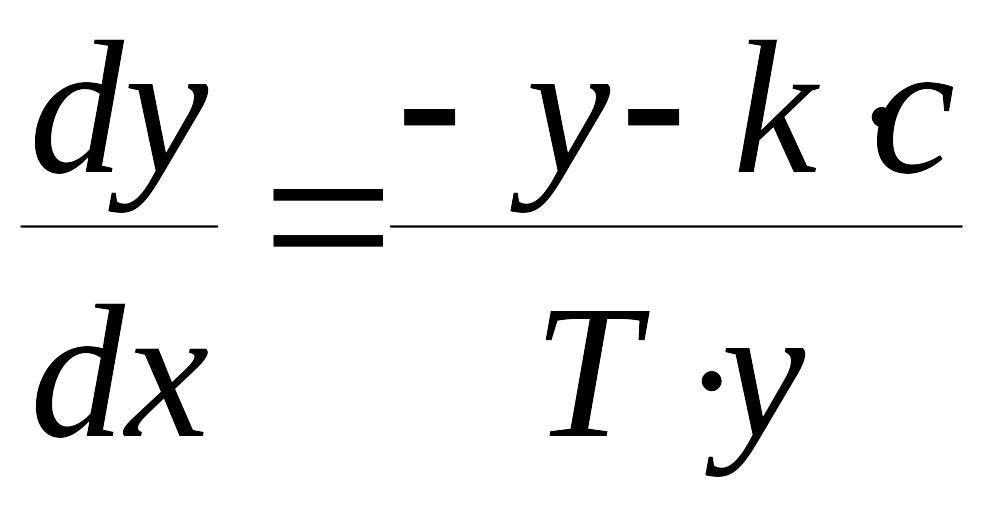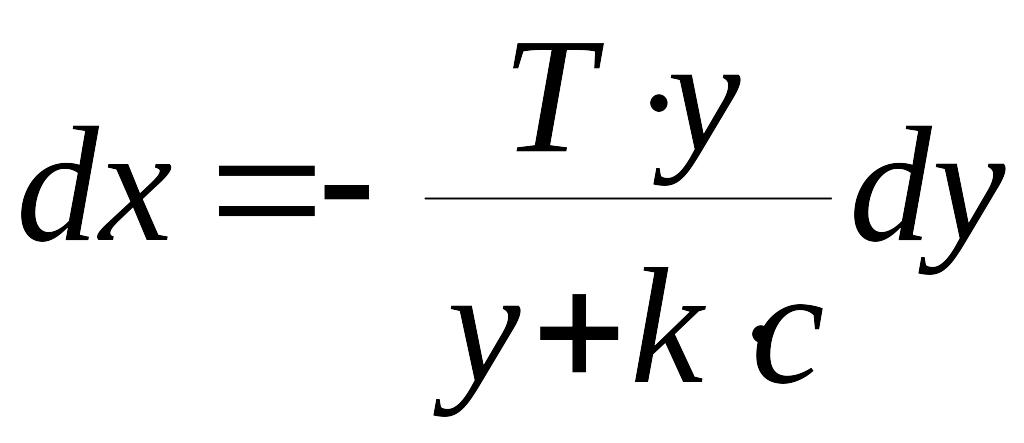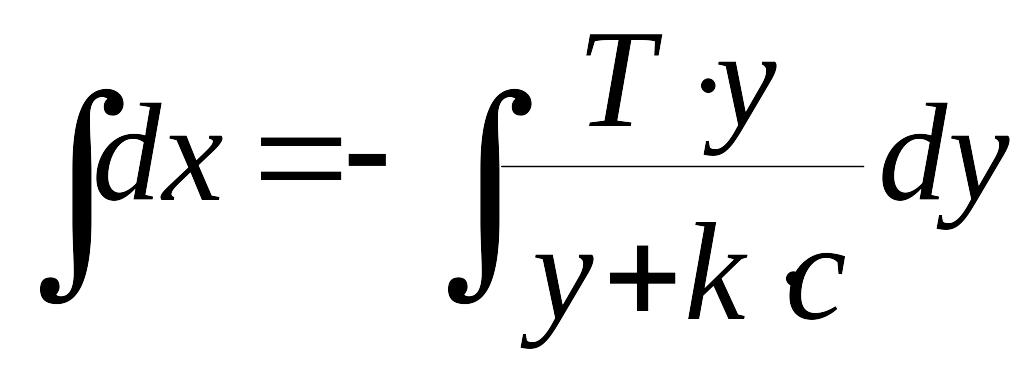Вычислим интеграл, стоящий в правой части полученного равенства

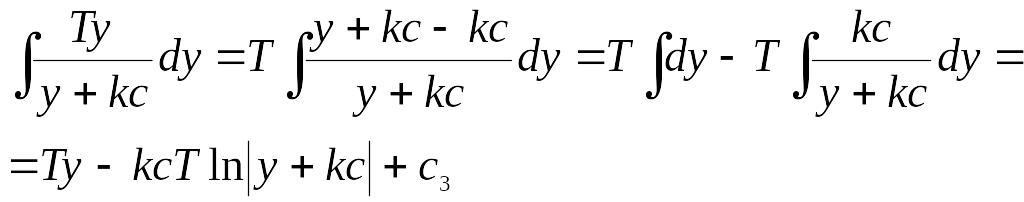
Таким образом, интегрирование уравнения (11) в области III дает следующий результат

, (12)

где – постоянная интегрирования, которая определяется начальными условиями. Уравнение (12) – это уравнение фазовых траекторий системы в области Ш. Из уравнения (12) следует, что фазовые траектории имеют асимптоту

. (8)

Движение изображающей точки по фазовым траекториям в верхней полуплоскости, где происходит слева направо; в нижней полуплоскости, где – справа налево. На рисунке изображены фазовые траектории системы для области III. Напомним, что для этой области .

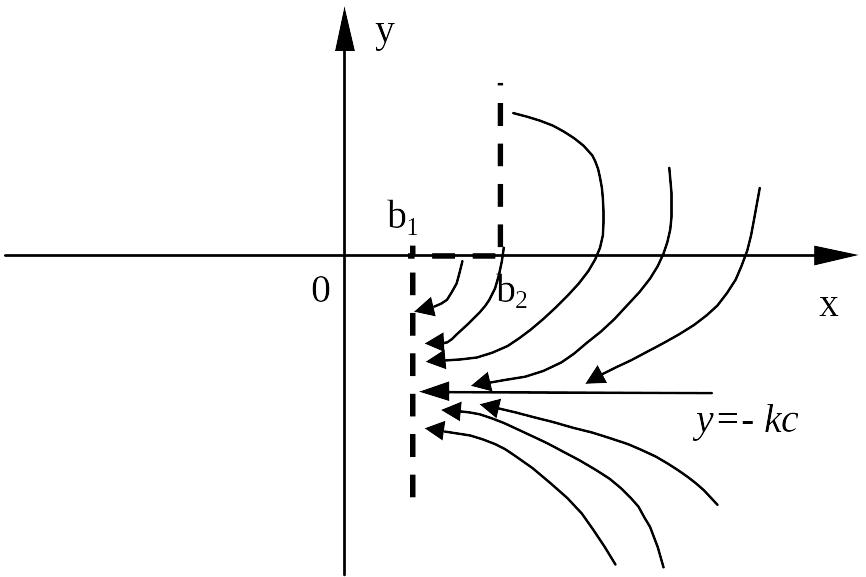
«Сшивая» области I, II и III фазовой плоскости по линии переключения получим фазовый портрет исследуемой системы.

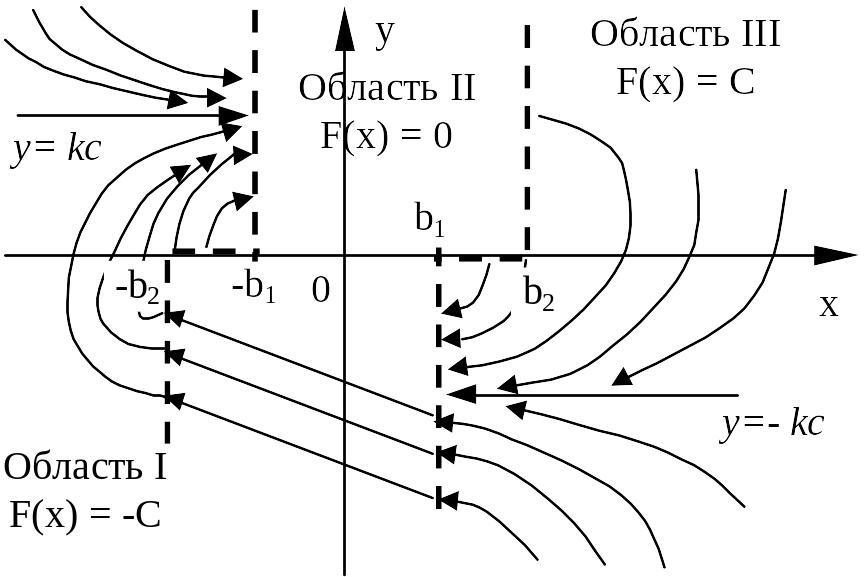
В целом фазовые траектории имеют спиралевидную форму. Это соответствует затухающим колебательным процессам. Но колебательный процесс затухает не до нуля, а до некоторого значения на интервале , при , т.е. внутри зоны нечувствительности реле.

По какой из фазовых траекторий пойдет переходный процесс в системе и каково установившееся значение выходной переменной определяется начальными условиями и имеет вид

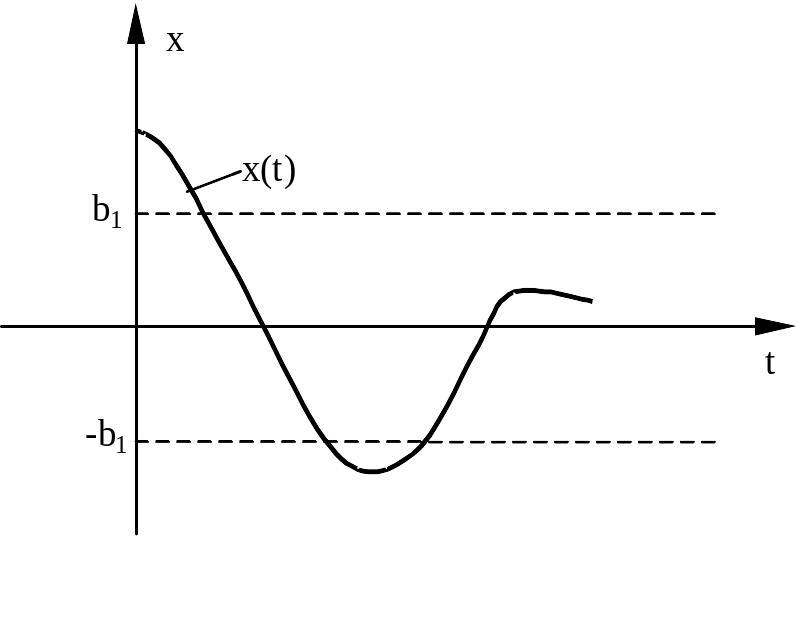
В рассматриваемом случае вместо особой точки получается ОСОБЫЙ отрезок равновесных состояний .Такой случай xарактерен только для нелинейных систем – отрезок состояний равновесия.

Практическое занятие 5. Вычисление коэффициентов гармонической линеаризации.

Задано нелинейное звено, которое описывается нелинейным уравнением .

Входная переменная нелинейного звена гармоническая функция

,

где – амплитуда, – частота. Период входного гармонического сигнала равен 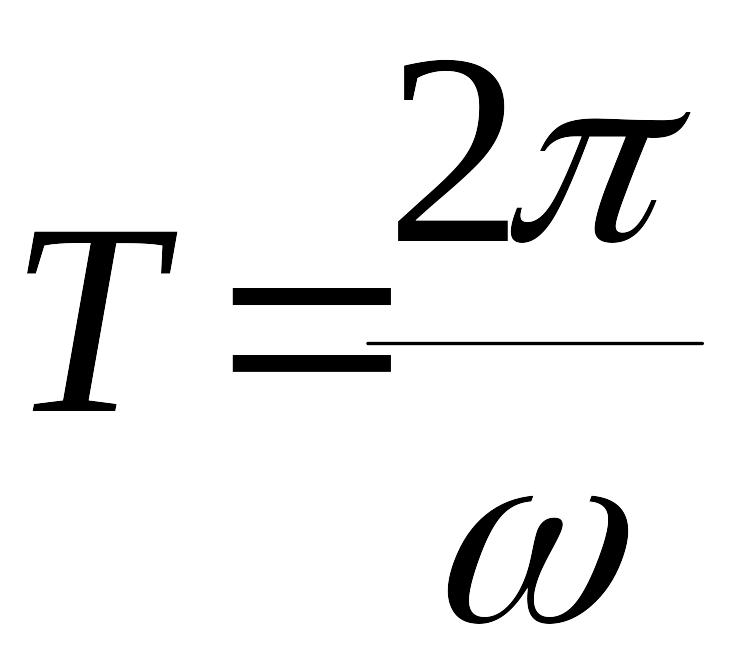. Выходной сигнал представляет собой периодическую функцию с периодом . Периодичность функций и одинакова.

Задача. Вычислить коэффициенты гармонической линеаризации и по формулам

,

,

где .

Цель вычисления коэффициентов гармонической линеаризации: замена нелинейного звена системы управления гармонически линеаризованным (квазилинейным) звеном с передаточной функцией .

При вычислении коэффициентов гармонической линеаризации следует:

1. Графо-аналитическим способом определить характерные особенности периодического сигнала на выходе нелинейного элемента

• Четность, нечетность периодической функции

• Характерные точки графика функции

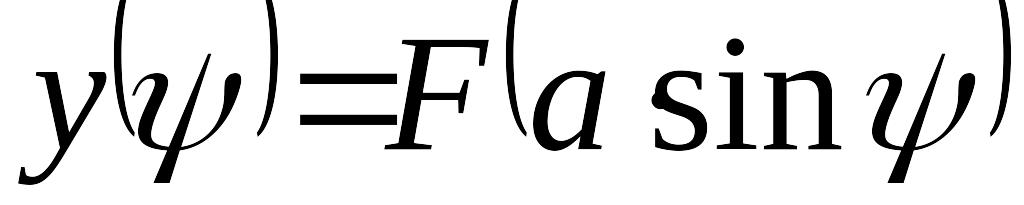
2. С учетом свойств функции вычислить коэффициенты гармонической линеаризации и по формулам

,

.

При вычислении коэффициентов гармонической линеаризации наиболее часто используются следующие тригонометрические равенства:

, , ,

, , ,

.

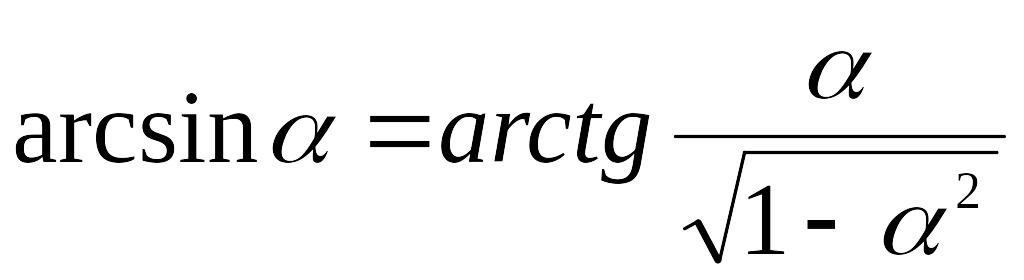ПРИМЕР. Вычислить коэффициенты гармонической линеаризации для нелинейного звена с релейной характеристикой общего вида.

, , .

,

,

,

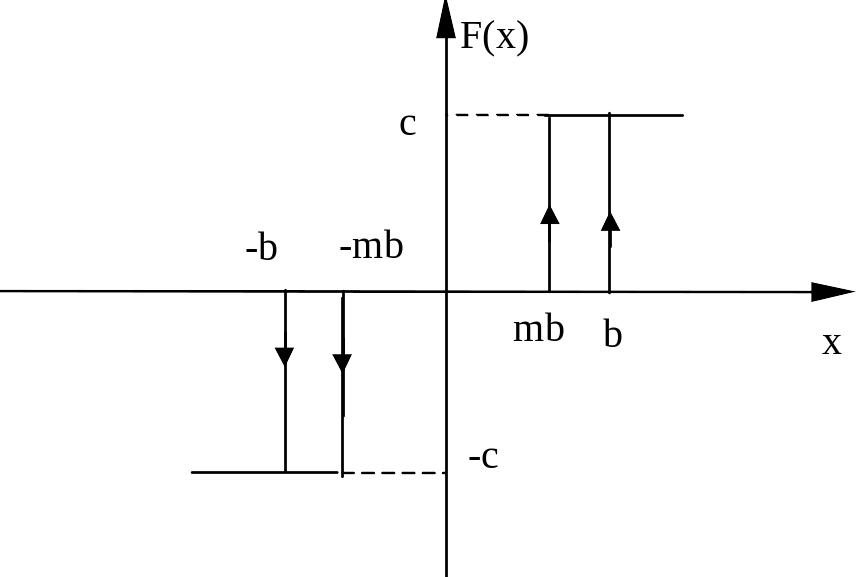
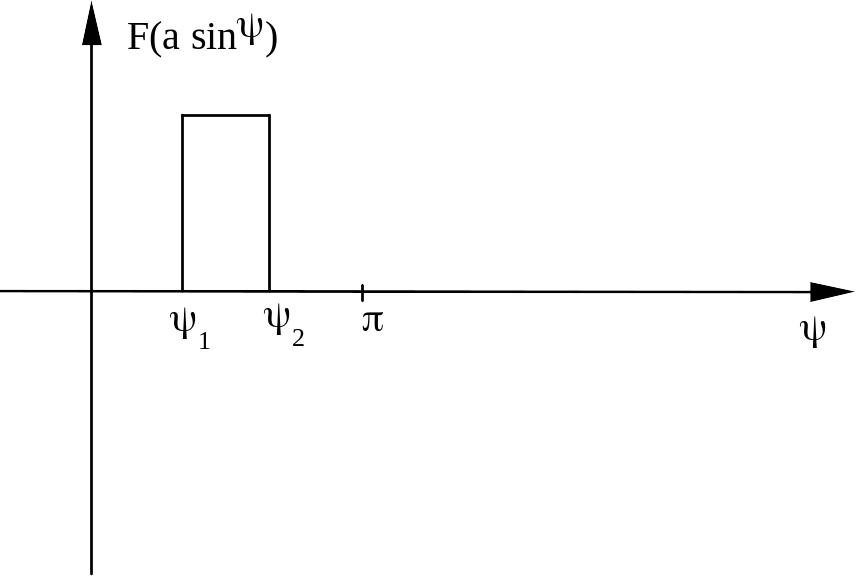
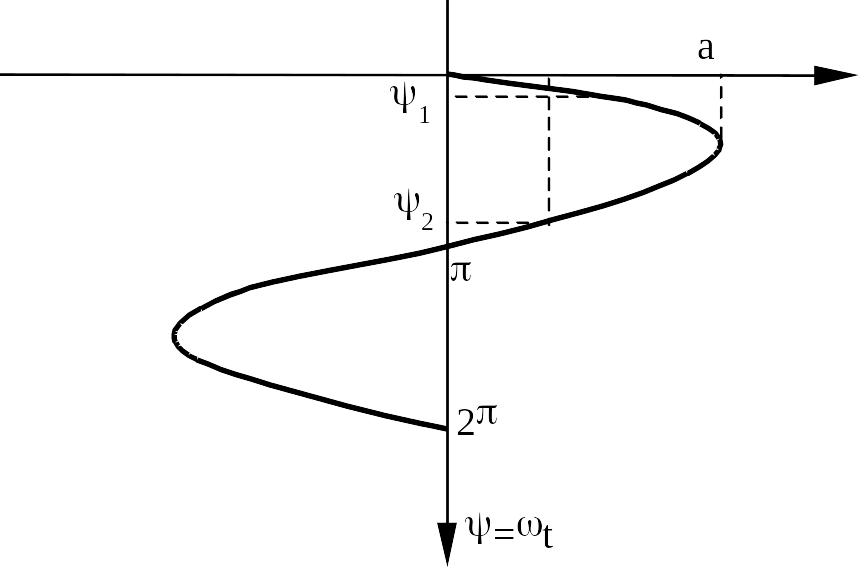
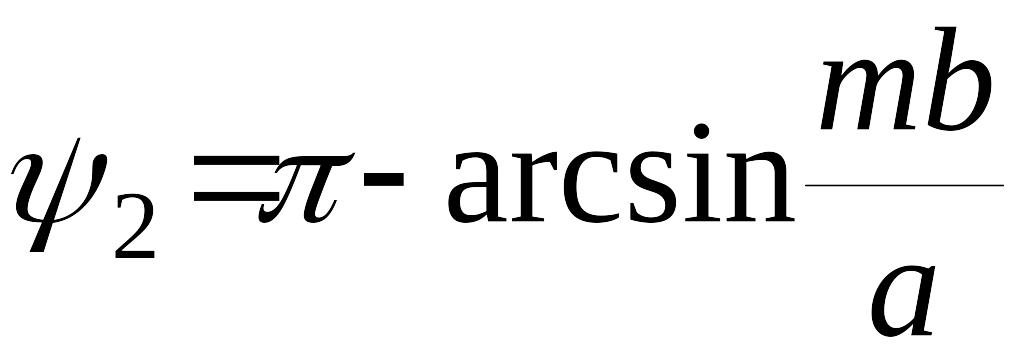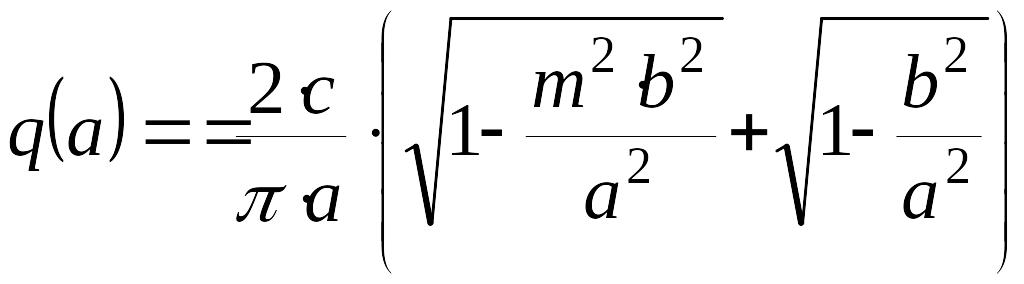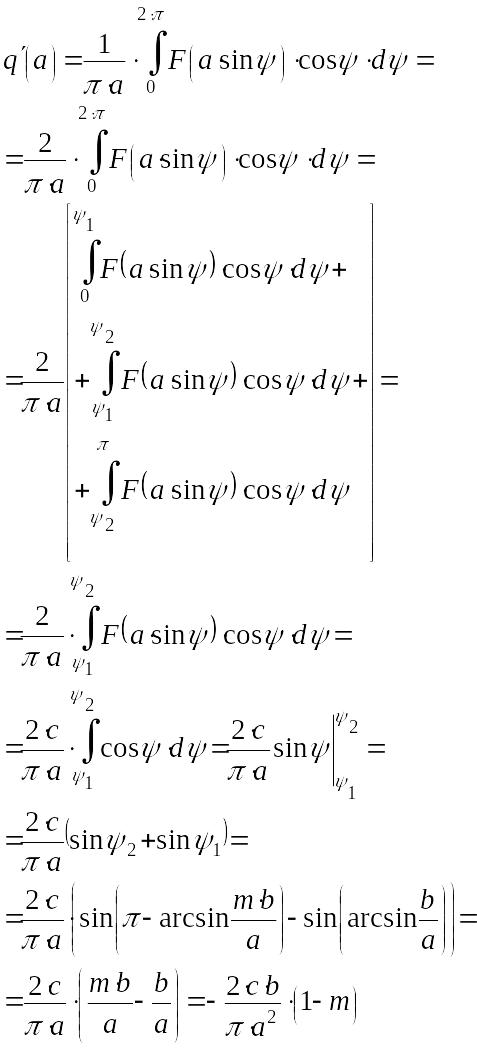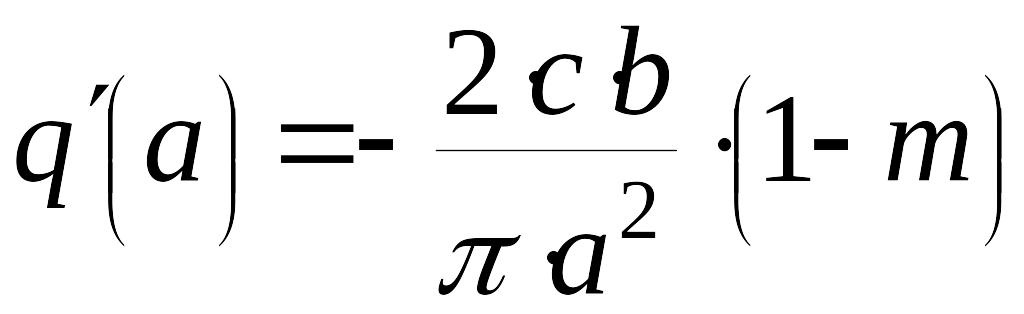
Практическое занятие 6. Переходные процессы в системе управления