
- •Содержание
- •Глоссарий
- •2. Конспект лекционных занятий лекция 1. Введение. Математические модели нелинейных элементов систем автоматического управления
- •Требования, предъявляемые к математическим моделям систем автоматического управления.
- •Математические модели нелинейных элементов систем автоматического управления.
- •Характеристика с насыщением (ограничение).
- •2. Реле с зоной нечувствительности.
- •3. Реле с гистерезисом.
- •4. Нелинейное звено типа "Люфт".
- •5. Нелинейное звено типа "Вязкое трение".
- •6. Нелинейное звено типа "Сухое трение".
- •Лекция 2. Основные особенности нелинейных систем автоматического управления
- •Основные методы исследования нелинейных систем:
- •Понятие о методе фазовой плоскости исследования нелинейных систем.
- •Лекция 3. Типы особых точек и фазовые портреты линейных систем второго порядка.
- •Лекция 4. Способы построения фазовых портретов нелинейных систем по уравнениям первого приближения.
- •Случай 1. Корни характеристического уравнения – чисто мнимые (Центр).
- •Корни характеристического уравнения
- •Случай 2. Корни характеристического уравнения – комплексно-сопряженные (фокус)
- •Случай 4 Корни характеристического уравнения действительны и разных знаков (седло)
- •Решение уравнения (1) аналогично предыдущему случаю имеет вид
- •Случай 5 Корни характеристического уравнения равны кратные (вырожденный узел ). Рассмотрим систему
- •Матрица динамики системы
- •Лекция 5. Линеаризация уравнений систем автоматического управления. Уравнения первого приближения.
- •Так как в особой точке справедливо и , то окончательно получаем
- •Фазовые траектории нелинейных систем автоматического управления.
- •Лекция 6. Построение фазовых портретов нелинейных систем управления по уравнениям первого приближения.
- •Лекция 7. Исследование процессов в нелинейных системах методом фазовой плоскости. Реле с гистерезисом и зоной нечувствительности.
- •Исследование процессов в нелинейных системах методом фазовой плоскости. Реле с гистерезисом.
- •Лекция 8. Исследование процессов в нелинейных системах методом фазовой плоскости. Скользящие процессы в релейных системах.
- •Вывод 3. Уравнение движения системы вдоль линии переключения
- •Процессы в релейных системах со скользящим режимом.
- •Лекция 9. Основы исследования систем автоматического управления методом гармонической линеаризации
- •Математическая модель исследуемой системы автоматического управления.
- •II. В системе возникли автоколебания.
- •Математическая основа метода гармонической линеаризации.
- •Свойство фильтра линейной части системы.
- •Коэффициенты гармонической линеаризации.
- •VI. Гармонически линеаризованное нелинейное звено.
- •Исследования автоколебаний в нелинейных системах методом гармонической линеаризации.
- •Лекция 10. Методы определения амплитуды и частоты автоколебаний в нелинейных системах автоматического управления
- •Исходные положения.
- •Линейная часть системы управления обладает свойством фильтра, т.Е. , , следовательно, переменную можно представить в виде , .
- •Лекция 11. Алгебраический метод определения параметров периодических решений нелинейных систем.
- •Частотные методы определения параметров периодических решений.
- •Лекция 12. Устойчивость периодического решения
- •Применение критерия Михайлова для исследования устойчивости периодического решения.
- •Аналитическая форма критерия устойчивости периодического решения.
- •Применение критерия Гурвица для исследования устойчивости периодического решения.
- •Решение. Гармоническая линеаризация нелинейного звена дает следующие коэффициенты гармонической линеаризации
- •Несимметричные автоколебания. Постоянные ошибки
- •Выделим отсюда уравнение для постоянных составляющей
- •Лекция 13. Исследование устойчивости нелинейных систем. Определение устойчивости, функции ляпунова.
- •Теоремы Ляпунова.
- •Лекция 14. Устойчивость нелинейных управляемых систем. Критерий в.-м. Попова.
- •Интерпретация функции .
- •Видоизмененная частотная характеристика.
- •Способ построения диаграмм качества.
- •Лабораторная работа № 1 Моделирование систем управления в пакете Simulink
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 2 Моделирование нелинейных систем управления Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 3 Программирование в среде Matlab Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 4 Оптимизация нелинейных систем Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 7 Цифровая реализация непрерывного регулятора Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •4. Практические занятия Практическое занятие 1. Разработка алгоритма исследования линейных систем автоматического управления методом фазовой плоскости.
- •Пример. Структурная схема системы автоматического управления имеет вид, показанный на рисунке
- •Влияние параметров системы управления на тип особой точки. Бифуркация.
- •Пример. Установить типы особых точек нелинейной системы
- •Решение. Определим координаты особых точек
- •Пример. Структурная схема системы автоматического управления имеет вид, показанный на рисунке
- •Решение. В соответствии с выше принятыми обозначениями
- •Самостоятельная работа студентов под руководством преподавателей (срсп). Срсп №1
- •Задание
- •Указания к выполнению
- •Задание к срсп №3 Тема: Дискретизация и наложение спектров (aliasing)
- •Задание к срсп №4 Тема: Восстановление дискретизированных Сигналов
- •Задание к срсп №5 Тема: Дуобинарное упражнение
- •Самостоятельная работа студентов
- •7. Экзаменационные вопросы
- •Понятие о методе фазовой плоскости исследования нелинейных систем.
- •Коэффициенты гармонической линеаризации.
- •Список рекомендуемой литературы Основная литература:
Основные методы исследования нелинейных систем:
Методы фазовой плоскости (фазового пространства).
Методы линеаризации (уравнения первого приближения, гармоническая линеаризация).
Специальные методы.
Понятие о методе фазовой плоскости исследования нелинейных систем.
Пусть нелинейная система автоматического управления описывается системой дифференциальных уравнений вида
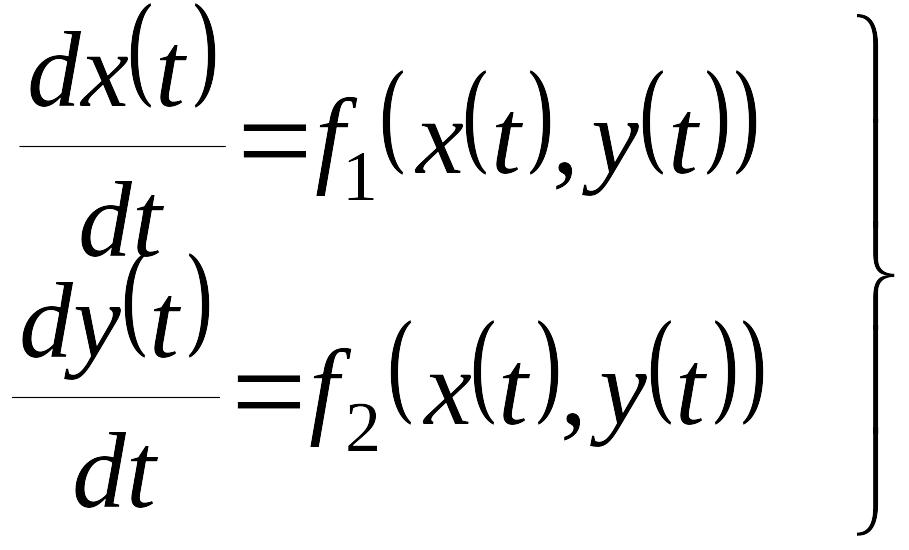 . (1)
. (1)
Далее
считаем, что начальные условия для
системы уравнений (1)
![]() и
и
![]() заданы.
заданы.
Состояние
системы в любой момент времени
характеризуется двумя значениями
![]() ,
,
![]() .
.
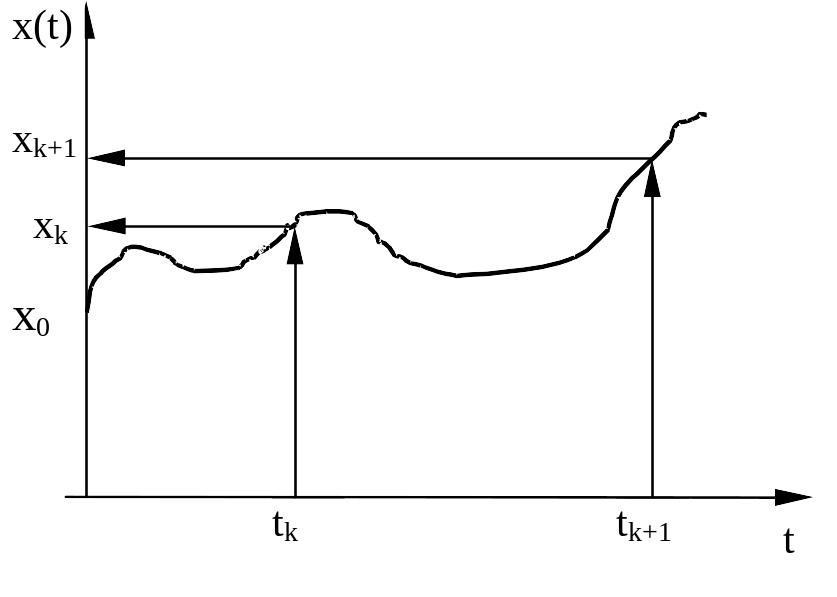
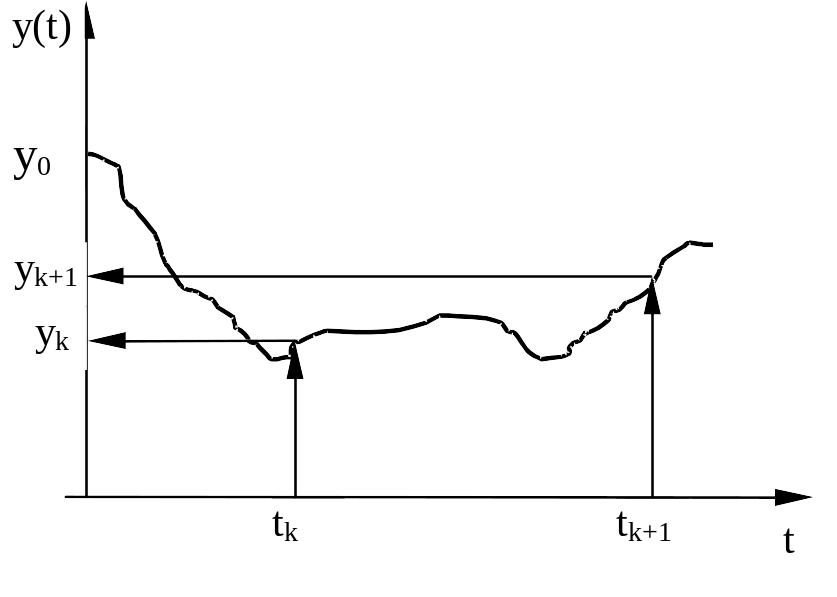
Введем
в рассмотрение плоскость с координатными
осями
![]() и
и
![]() .
Зафиксируем момент времени
.
Зафиксируем момент времени
![]() и вычислим при этом значении времени
величины
и вычислим при этом значении времени
величины
![]() и
и
![]() .
В плоскости
.
В плоскости
![]() отметим точку
отметим точку
![]() с координатами
с координатами
![]() .
Вычислим следующее значение времени
.
Вычислим следующее значение времени
![]() ,
где
,
где
![]() – постоянное число. При этом значении
– постоянное число. При этом значении
![]() аналогично предыдущему определим
значения
аналогично предыдущему определим
значения
![]() и
и
![]() .
.
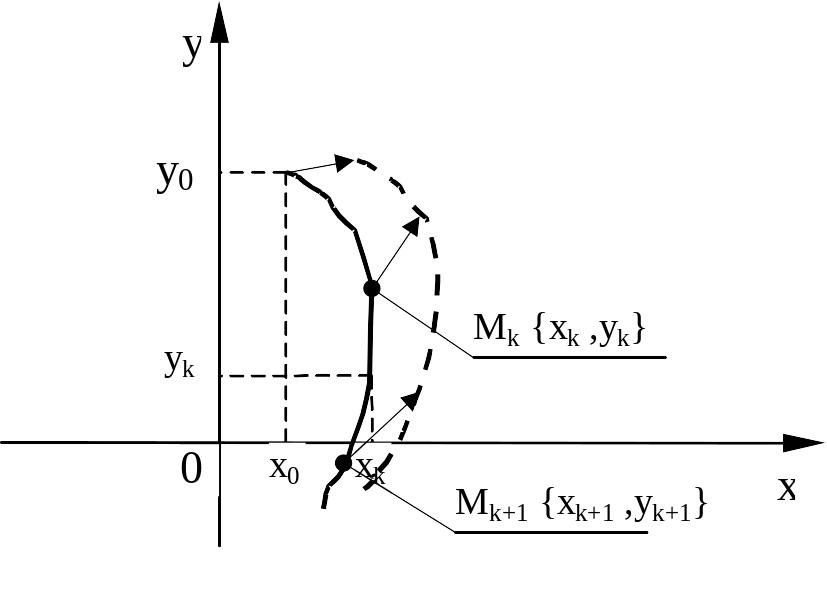
На
плоскости
нанесем точку с координатами
с координатами
![]() .
Проведем вышеописанное построение для
.
Проведем вышеописанное построение для
![]() .
В результате чего получим на плоскости
последовательность точек
.
В результате чего получим на плоскости
последовательность точек
![]() ,
,
![]() ,…,
,
соединив которые получим графическое
изображение кривой
,…,
,
соединив которые получим графическое
изображение кривой
![]() ,
которая называется фазовой траекторией
нелинейной системы (1).
,
которая называется фазовой траекторией
нелинейной системы (1).
Точка
![]() называется изображающей
точкой –
при изменении
от 0 до
называется изображающей
точкой –
при изменении
от 0 до![]() изображающая точка на плоскости
описывает кривую – фазовую
траекторию.
Плоскость
– называется
фазовой плоскостью.
изображающая точка на плоскости
описывает кривую – фазовую
траекторию.
Плоскость
– называется
фазовой плоскостью.
Каждому
новому значению начальных условий
![]() будет соответствовать на фазовой
плоскости своя
фазовая траектория.
будет соответствовать на фазовой
плоскости своя
фазовая траектория.
Множество фазовых траекторий на фазовой плоскости называется фазовым портретом системы автоматического управления.
Значение
нелинейных функций
![]() и
и
![]() ,
стоящие в правой части системы (1) в
каждый момент времени
,
стоящие в правой части системы (1) в
каждый момент времени
![]() определяют проекции скорости движения
изображающей точки на оси координат
и
соответственно. Это потому, что они
согласно дифференциальным уравнениям
(1) соответственно равны
определяют проекции скорости движения
изображающей точки на оси координат
и
соответственно. Это потому, что они
согласно дифференциальным уравнениям
(1) соответственно равны
![]() и
и
![]() .
.
На
фазовой плоскости
существуют характерные точки, которые
определяются нулевыми значениями
проекции вектора скорости:
![]() ,
,
![]() ,
следовательно
,
следовательно
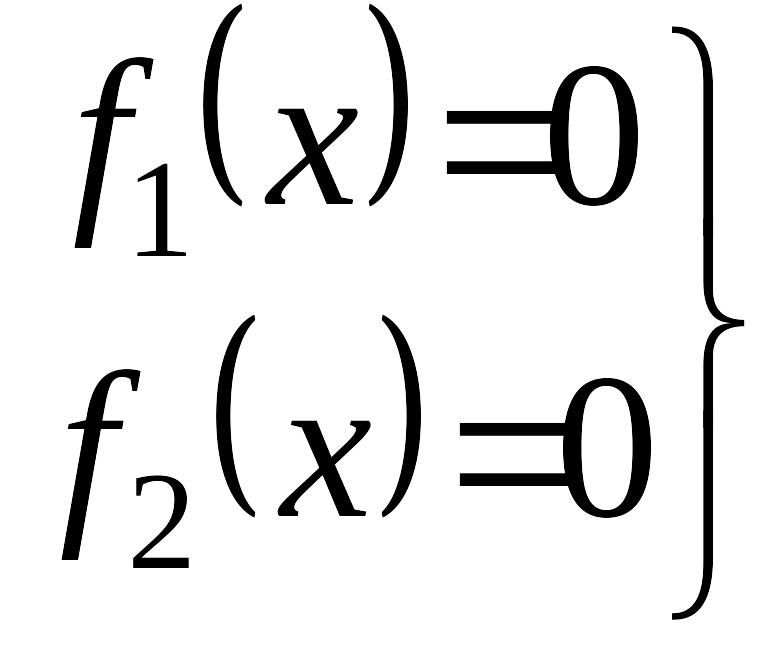 (2)
(2)
Координаты особых точек определяются как решение системы нелинейных алгебраических уравнений (2). Их может быть несколько.
Пример. Математическая модель системы управления задана уравнениями
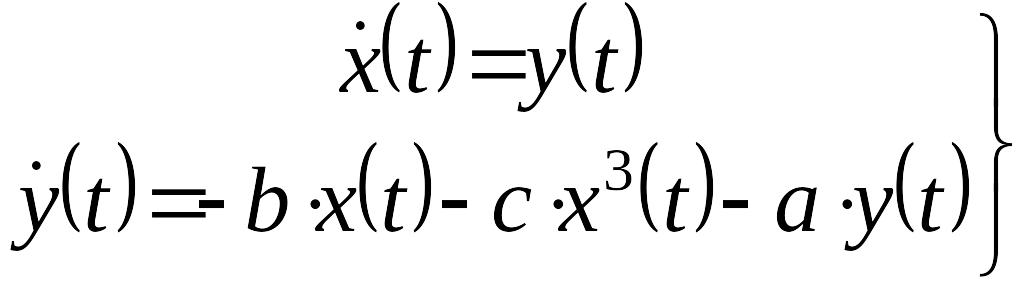 .
.
Требуется найти координаты особых точек (точек равновесного состояния).
Решение.
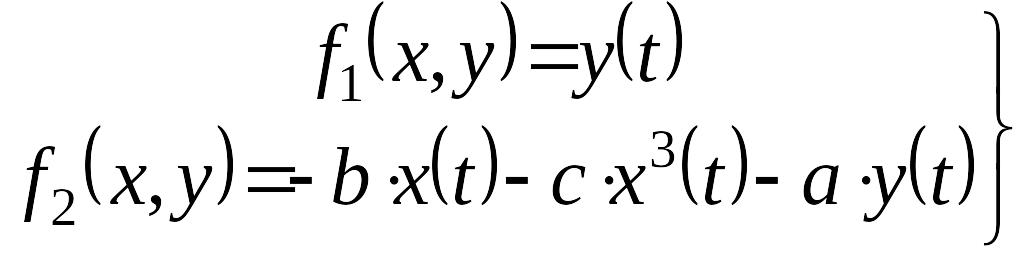 ,
,
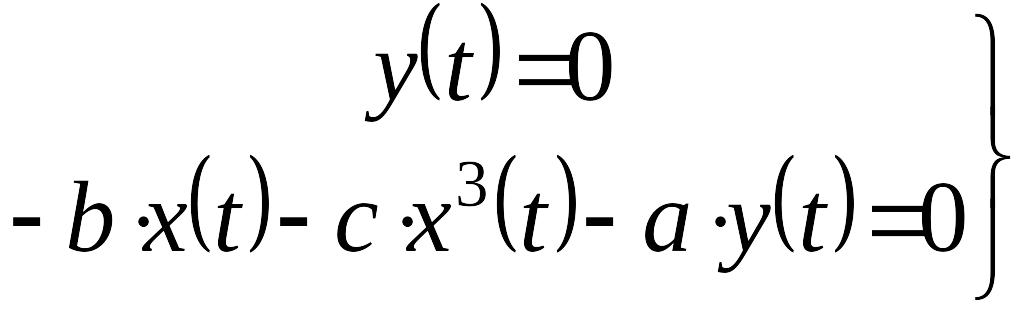
Это система уравнений для определения координат особых точек. Решим ее:
![]() ,
,
![]() ,
,
![]() .
.
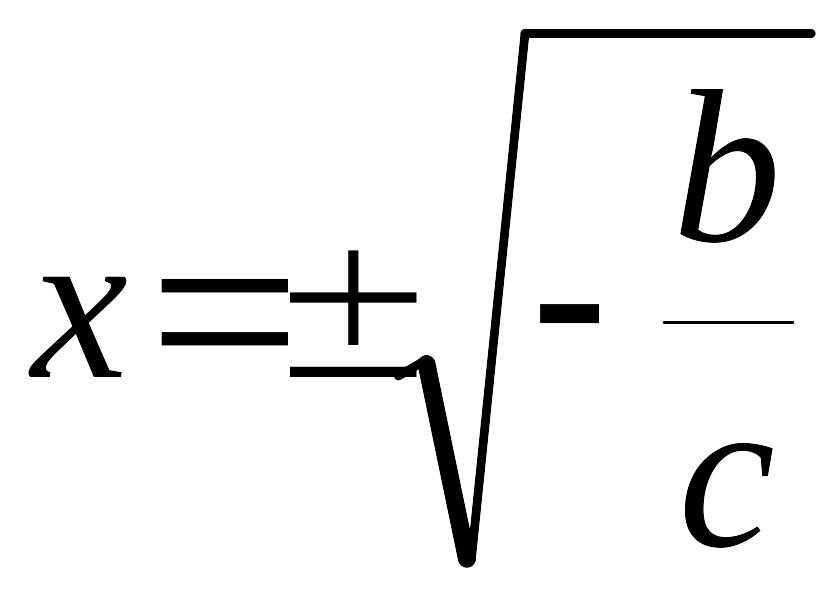 .
.
Система
обладает тремя состояниями равновесия
при условии, что параметры системы
и
![]() имеют разные знаки.
имеют разные знаки.
![]()
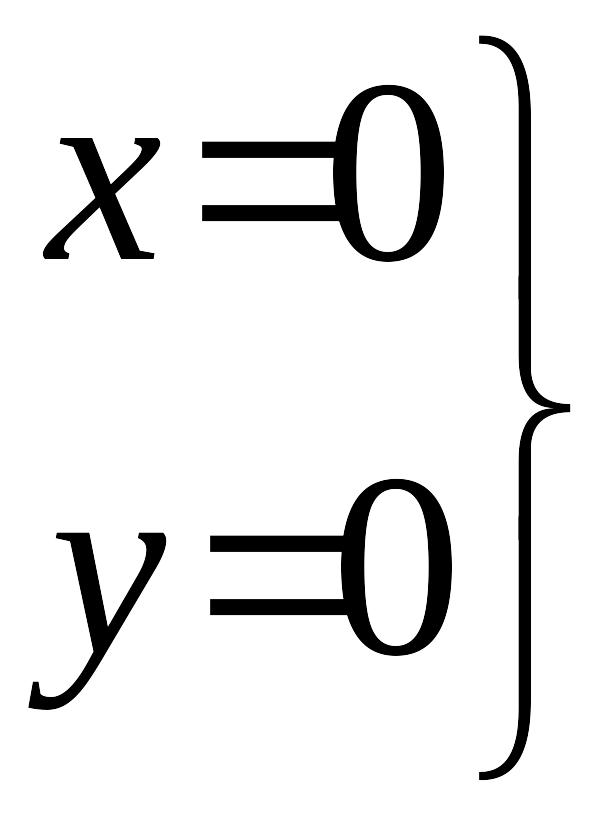 Координаты
первой особой точки.
Координаты
первой особой точки.
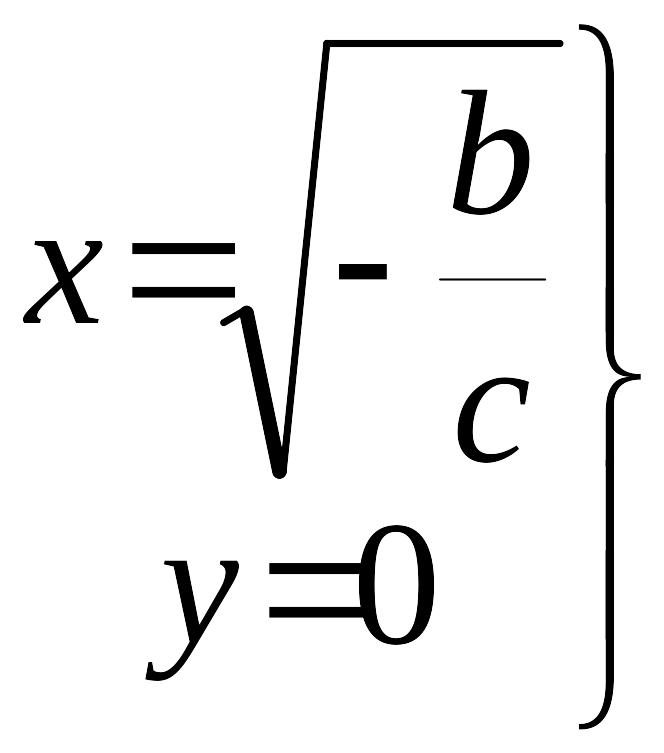 Координаты
второй особой точки
Координаты
второй особой точки
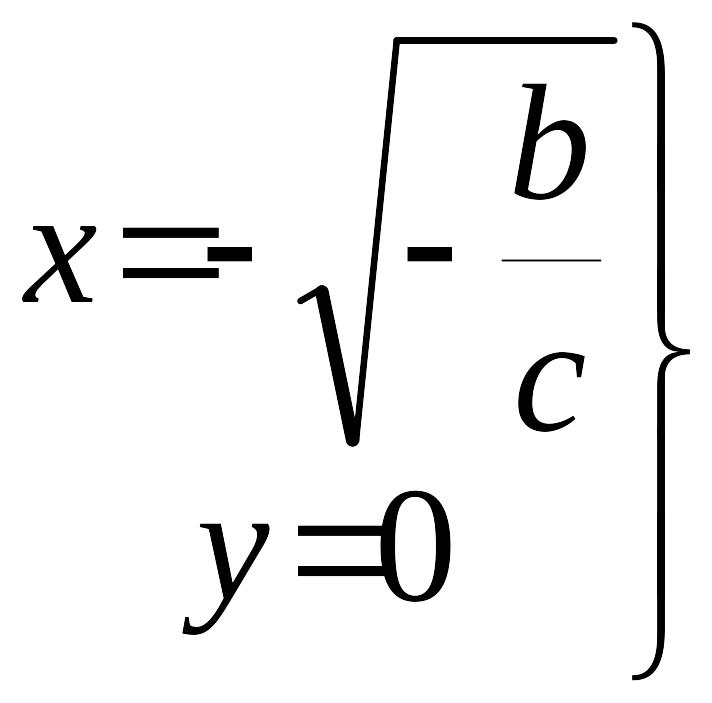 Координаты
третьей особой точки
Координаты
третьей особой точки
Если
и
– имеют одинаковые знаки, то у системы
одна точка состояния равновесия, ее
координаты -
и
![]() .
.
В особых точках вектор фазовой скорости нулевой. Это – состояния равновесия системы.
Равенство нулю вектора фазовой скорости создает неопределенность в правой части системы уравнений (1). Поэтому точки равновесия системы называются особыми точками системы на фазовой плоскости.
На фазовых траекториях как правило указывают направление движения изображающей точки. Направление движения определяется направлением фазовой скорости.
Если система дифференциальных уравнений (1) имеет вид
![]() ,
,
![]() , (3)
, (3)
то в этом случае можно сформулировать правило для определения направления движения изображающей точки по фазовым траекториям
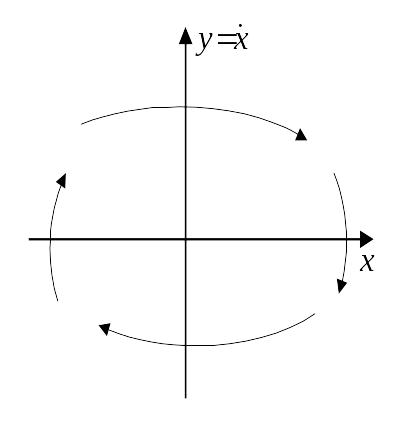
в верхней плоскости движение происходит слева направо, т.е. в сторону увеличения
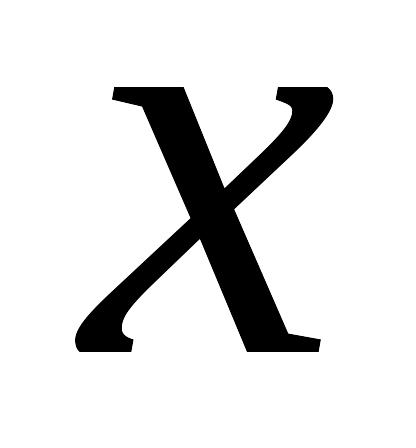 ,
т.к. там
,
т.к. там
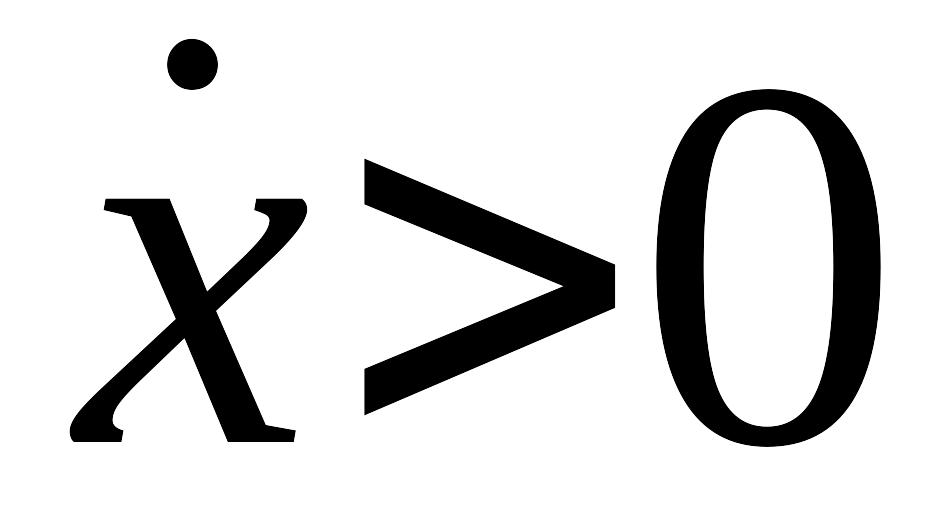
в нижней полуплоскости – движение справа налево, т.к. здесь
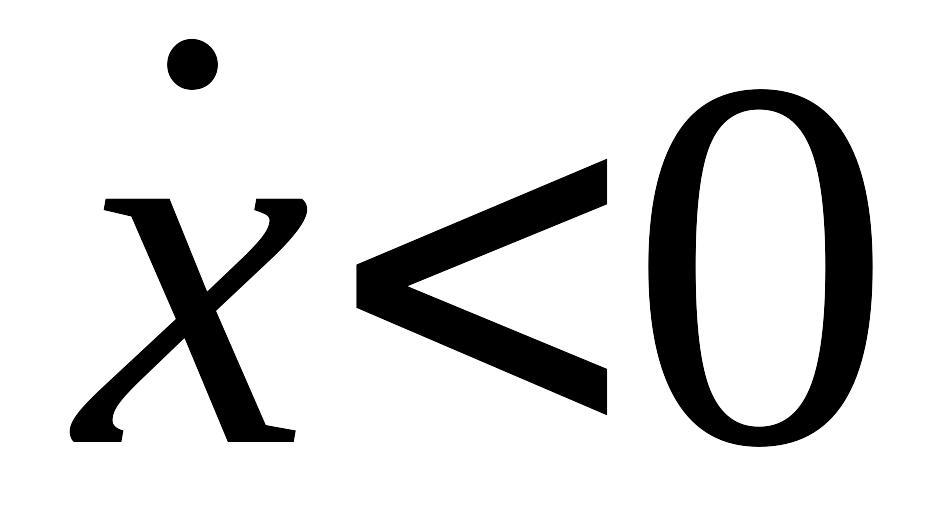 ,
величина
– уменьшается.
,
величина
– уменьшается.ось пересекается фазовыми траекториями под прямым углом, т.к. там скорость
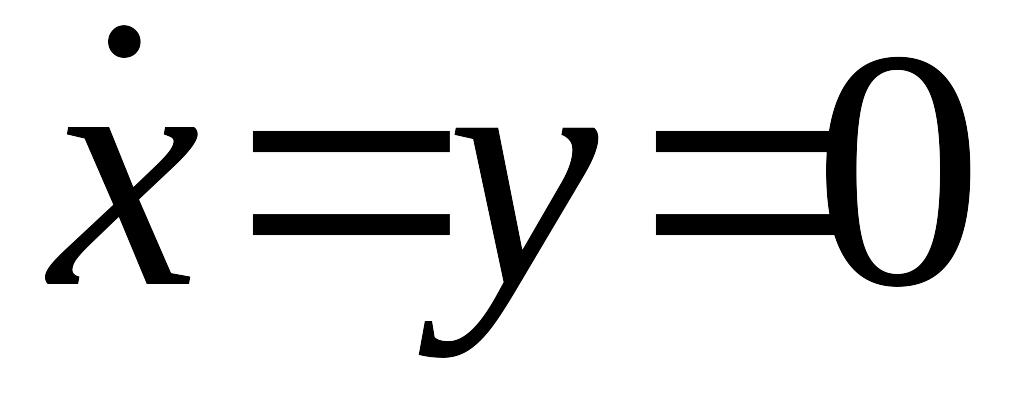 ,
т.е. имеет место максимум или минимум
величины
.
,
т.е. имеет место максимум или минимум
величины
.
(Правило не действительно в общем случае уравнений (1)).
Из системы дифференциальных уравнений (1) можно получить дифференциальные уравнения фазовых траекторий. Для того чтобы получить дифференциальные уравнения фазовых траекторий системы (1) нужно из них исключить время. Это достигается делением второго уравнения системы (1) на первое
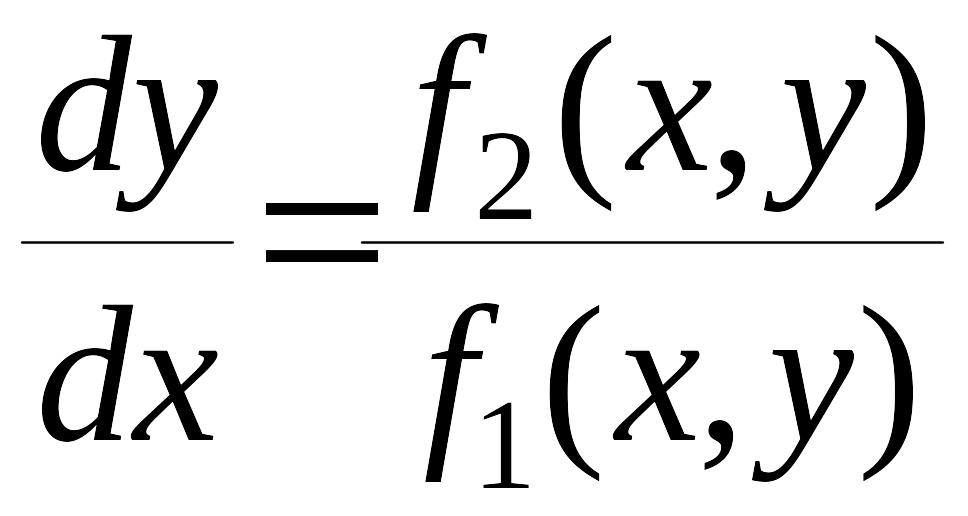 .
.
Существует соответствие между фазовыми траекториями системы управления и видом переходного процесса и наоборот.
Для
простоты рассмотрим систему уравнений
(3) и пусть состояние равновесия системы
– это точка на фазовой плоскости с
координатами
![]() .
.
Пусть далее, фазовая траектория системы имеет вид, показанный на рисунке. По заданной фазовой траектории построим переходный процесс в исследуемой системе (3)
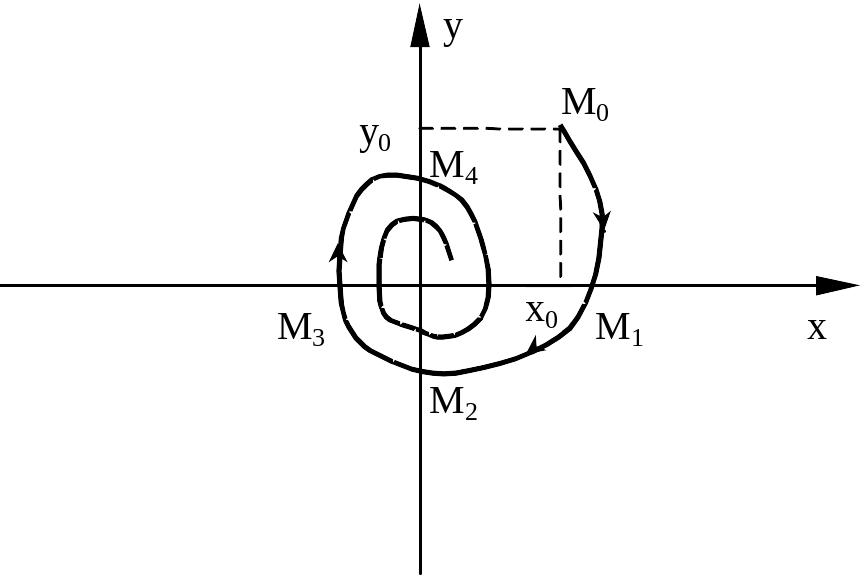
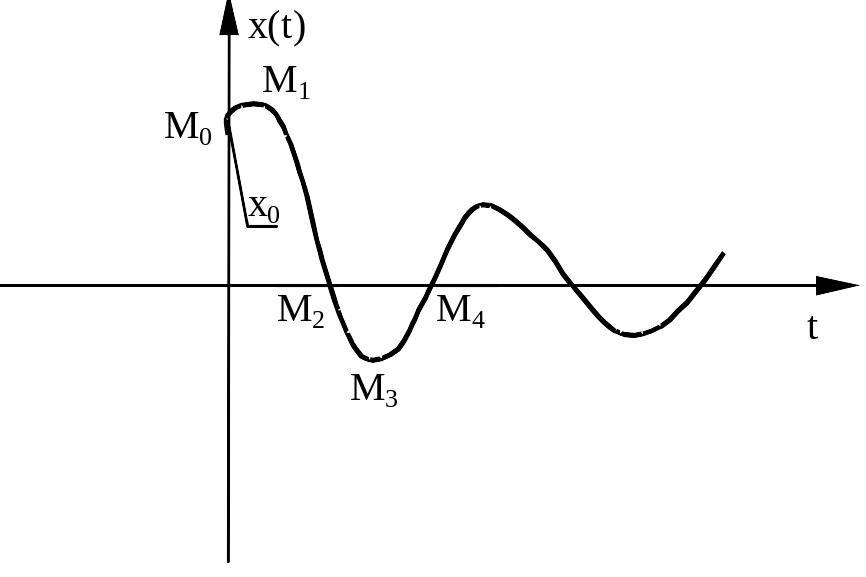
На фазовой траектории отметим характерные точки:
![]() – начальные
условия;
– начальные
условия;
![]() – возможен
экстремум,
– возможен
экстремум,
![]() или
или
![]()
![]() – значение
– график
пересекает ось
– значение
– график
пересекает ось
![]() .
.
![]() – возможен экстремум
графика функции
.
– возможен экстремум
графика функции
.
![]() – значение
– график функции
пересекает ось
.
– значение
– график функции
пересекает ось
.
Точка
находится первом квадрате
![]() ,
,
![]() .
Между точками
.
Между точками
![]()
![]() ,
следовательно
возрастает, между
,
следовательно
возрастает, между
![]()
![]() ,
следовательно
убывает. Это значит, что точке
соответствует максимум графика функции
.
Точке
,
следовательно
убывает. Это значит, что точке
соответствует максимум графика функции
.
Точке
![]() – соответствует точка пересечения
графика функции
оси
.
Между точками
– соответствует точка пересечения
графика функции
оси
.
Между точками
![]() ,
следовательно
продолжает убывать. Между точками
,
следовательно
продолжает убывать. Между точками
![]() y
> 0 и
начинает возрастать. Это значит, что
y
> 0 и
начинает возрастать. Это значит, что
![]() – соответствует точке минимума графика
функции
.
Точке
– соответствует точке минимума графика
функции
.
Точке
![]() соответствует точка пересечения графика
функции
оси
.
Продолжая аналогичные построения можно
построить весь переходный процесс.
соответствует точка пересечения графика
функции
оси
.
Продолжая аналогичные построения можно
построить весь переходный процесс.
По
переходному процессу можно построить
фазовую траекторию. Для этого в точках
,
,
…, вычисляют значение
![]() – производной
.
Считая, что эти вычисленные значения
,
– производной
.
Считая, что эти вычисленные значения
,
![]() – это координаты изображающей точки
наносим их на фазовую плоскость. Соединив
их, получим фазовую траекторию исследуемой
системы.
– это координаты изображающей точки
наносим их на фазовую плоскость. Соединив
их, получим фазовую траекторию исследуемой
системы.
Удобство изображения фазовых траекторий на плоскости состоит в том, что в виде единого «фазового портрета» представляется вся совокупность возможных форм процессов в системе управления.
Недостатком является то, что мы вынуждены ограничиваться рассмотрением лишь системами второго порядка. Для исследования систем высокого порядка применяются другие методы.
