- •Содержание
- •Глоссарий
- •2. Конспект лекционных занятий лекция 1. Введение. Математические модели нелинейных элементов систем автоматического управления
- •Требования, предъявляемые к математическим моделям систем автоматического управления.
- •Математические модели нелинейных элементов систем автоматического управления.
- •Характеристика с насыщением (ограничение).
- •2. Реле с зоной нечувствительности.
- •3. Реле с гистерезисом.
- •4. Нелинейное звено типа "Люфт".
- •5. Нелинейное звено типа "Вязкое трение".
- •6. Нелинейное звено типа "Сухое трение".
- •Лекция 2. Основные особенности нелинейных систем автоматического управления
- •Основные методы исследования нелинейных систем:
- •Понятие о методе фазовой плоскости исследования нелинейных систем.
- •Лекция 3. Типы особых точек и фазовые портреты линейных систем второго порядка.
- •Лекция 4. Способы построения фазовых портретов нелинейных систем по уравнениям первого приближения.
- •Случай 1. Корни характеристического уравнения – чисто мнимые (Центр).
- •Корни характеристического уравнения
- •Случай 2. Корни характеристического уравнения – комплексно-сопряженные (фокус)
- •Случай 4 Корни характеристического уравнения действительны и разных знаков (седло)
- •Решение уравнения (1) аналогично предыдущему случаю имеет вид
- •Случай 5 Корни характеристического уравнения равны кратные (вырожденный узел ). Рассмотрим систему
- •Матрица динамики системы
- •Лекция 5. Линеаризация уравнений систем автоматического управления. Уравнения первого приближения.
- •Так как в особой точке справедливо и , то окончательно получаем
- •Фазовые траектории нелинейных систем автоматического управления.
- •Лекция 6. Построение фазовых портретов нелинейных систем управления по уравнениям первого приближения.
- •Лекция 7. Исследование процессов в нелинейных системах методом фазовой плоскости. Реле с гистерезисом и зоной нечувствительности.
- •Исследование процессов в нелинейных системах методом фазовой плоскости. Реле с гистерезисом.
- •Лекция 8. Исследование процессов в нелинейных системах методом фазовой плоскости. Скользящие процессы в релейных системах.
- •Вывод 3. Уравнение движения системы вдоль линии переключения
- •Процессы в релейных системах со скользящим режимом.
- •Лекция 9. Основы исследования систем автоматического управления методом гармонической линеаризации
- •Математическая модель исследуемой системы автоматического управления.
- •II. В системе возникли автоколебания.
- •Математическая основа метода гармонической линеаризации.
- •Свойство фильтра линейной части системы.
- •Коэффициенты гармонической линеаризации.
- •VI. Гармонически линеаризованное нелинейное звено.
- •Исследования автоколебаний в нелинейных системах методом гармонической линеаризации.
- •Лекция 10. Методы определения амплитуды и частоты автоколебаний в нелинейных системах автоматического управления
- •Исходные положения.
- •Линейная часть системы управления обладает свойством фильтра, т.Е. , , следовательно, переменную можно представить в виде , .
- •Лекция 11. Алгебраический метод определения параметров периодических решений нелинейных систем.
- •Частотные методы определения параметров периодических решений.
- •Лекция 12. Устойчивость периодического решения
- •Применение критерия Михайлова для исследования устойчивости периодического решения.
- •Аналитическая форма критерия устойчивости периодического решения.
- •Применение критерия Гурвица для исследования устойчивости периодического решения.
- •Решение. Гармоническая линеаризация нелинейного звена дает следующие коэффициенты гармонической линеаризации
- •Несимметричные автоколебания. Постоянные ошибки
- •Выделим отсюда уравнение для постоянных составляющей
- •Лекция 13. Исследование устойчивости нелинейных систем. Определение устойчивости, функции ляпунова.
- •Теоремы Ляпунова.
- •Лекция 14. Устойчивость нелинейных управляемых систем. Критерий в.-м. Попова.
- •Интерпретация функции .
- •Видоизмененная частотная характеристика.
- •Способ построения диаграмм качества.
- •Лабораторная работа № 1 Моделирование систем управления в пакете Simulink
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 2 Моделирование нелинейных систем управления Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 3 Программирование в среде Matlab Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 4 Оптимизация нелинейных систем Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Лабораторная работа № 7 Цифровая реализация непрерывного регулятора Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •4. Практические занятия Практическое занятие 1. Разработка алгоритма исследования линейных систем автоматического управления методом фазовой плоскости.
- •Пример. Структурная схема системы автоматического управления имеет вид, показанный на рисунке
- •Влияние параметров системы управления на тип особой точки. Бифуркация.
- •Пример. Установить типы особых точек нелинейной системы
- •Решение. Определим координаты особых точек
- •Пример. Структурная схема системы автоматического управления имеет вид, показанный на рисунке
- •Решение. В соответствии с выше принятыми обозначениями
- •Самостоятельная работа студентов под руководством преподавателей (срсп). Срсп №1
- •Задание
- •Указания к выполнению
- •Задание к срсп №3 Тема: Дискретизация и наложение спектров (aliasing)
- •Задание к срсп №4 Тема: Восстановление дискретизированных Сигналов
- •Задание к срсп №5 Тема: Дуобинарное упражнение
- •Самостоятельная работа студентов
- •7. Экзаменационные вопросы
- •Понятие о методе фазовой плоскости исследования нелинейных систем.
- •Коэффициенты гармонической линеаризации.
- •Список рекомендуемой литературы Основная литература:
Описание системы
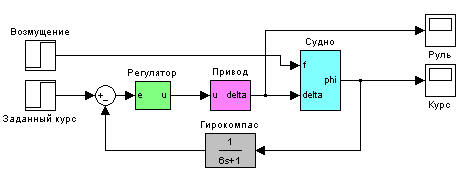
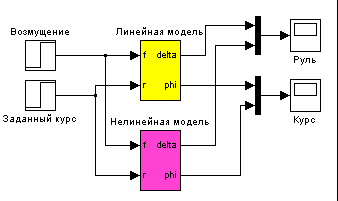
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.

Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
![]() ,
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
![]() ,
,
![]() .
.
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией4
,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией5
,
где
![]() сек
и
сек
и
![]() сек.
сек.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ
по кнопке
|
|
View – Current directory |
|
двойной щелчок на lab3.mdl |
|
File – Save as ... |
|
Edit – Create subsystem |
|
Двойной щелчок на имени ПКМ – Format – Flip name ПКМ – Background color |
|
Двойной щелчок на блоке ЛКМ на имени входа или выхода |
|
|
|
Edit – Create subsystem |
|
Перетащить с помощью ПКМ Format – Background color |
|
Двойной щелчок на блоке |
|
ЛКМ на элементе, нажать Delete. |
|
Двойной щелчок на блоке
|
|
View – Library Browser |
|
Двойной щелчок на блоке |+- в поле List of signs |
|
|
|
Двойной щелчок на блоке
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
File – New – M-file |
|
figure(1); % открыть рис. 1 subplot(2,1,1); plot(phi(:,1),phi(:,2),'b'); hold on; plot(phi(:,1),phi(:,3),'g'); hold off; legend('Линейная система', ... 'Нелинейная система') |
|
File - Save |
|
клавиша F5 |
|
set(gca,'FontSize',16); |
|
title('Поворот на 10 градусов') xlabel('Время, сек'); ylabel('\phi, град'); |
|
h = get(gca, 'Children') set(h(1),'LineWidth',1.5) set(h(2),'LineWidth',1.5) |
|
|
|
|
|
|
|
Двойной щелчок на блоке Заданный курс ввести 90 в поле Final value |
|
title('Поворот на 90 градусов') клавиша F5 print -dmeta |
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |