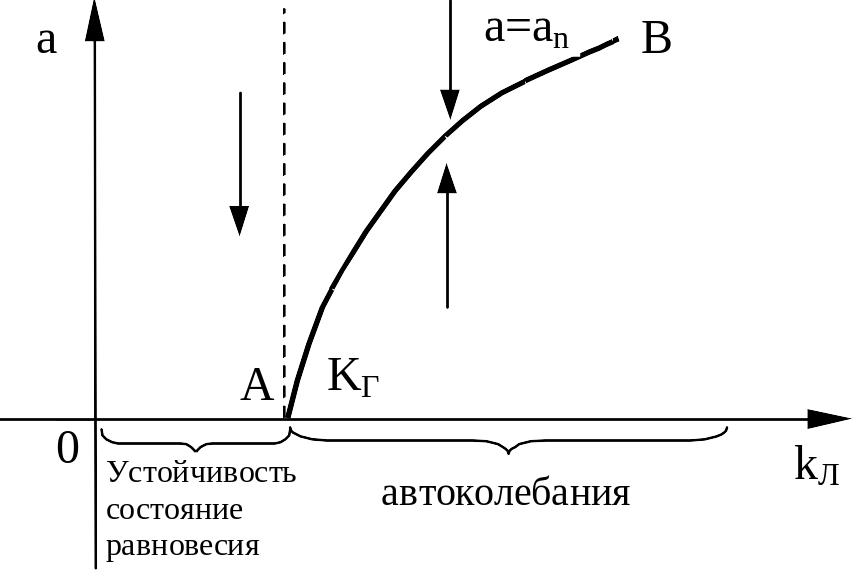
Способ построения диаграмм качества.

Пусть в какой-либо системе мы опреде­лили зависимость амплитуды автоколебаний от параметра , (см рис).

Здесь по параметру выделена область равновесного состояния. В автоколебательном режиме имеем

Ниже линии колебания расходятся. Следовательно, там . Выше линии колебания затухают и, значит, там . На самой линии имеем .

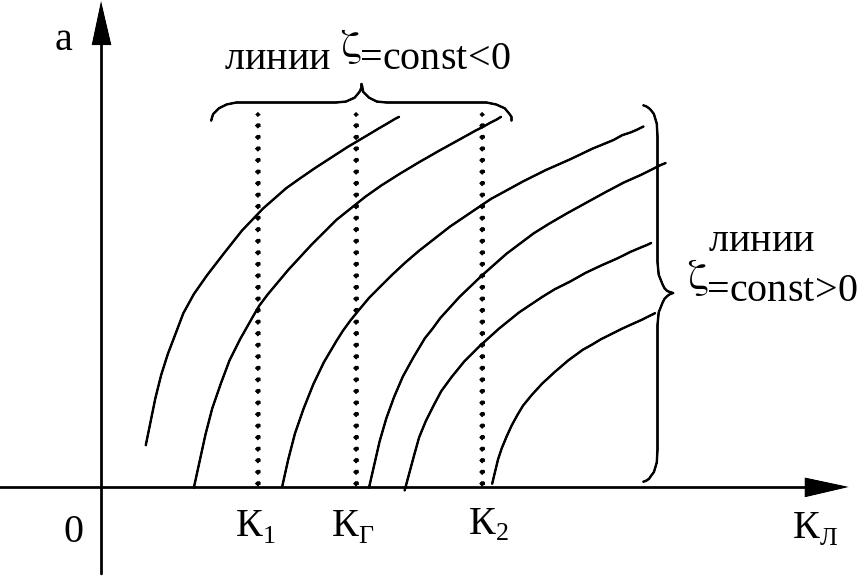
Если на основании уравнений (7) провести линии равных значений , то получится диаграмма, изображенная на рисунке.

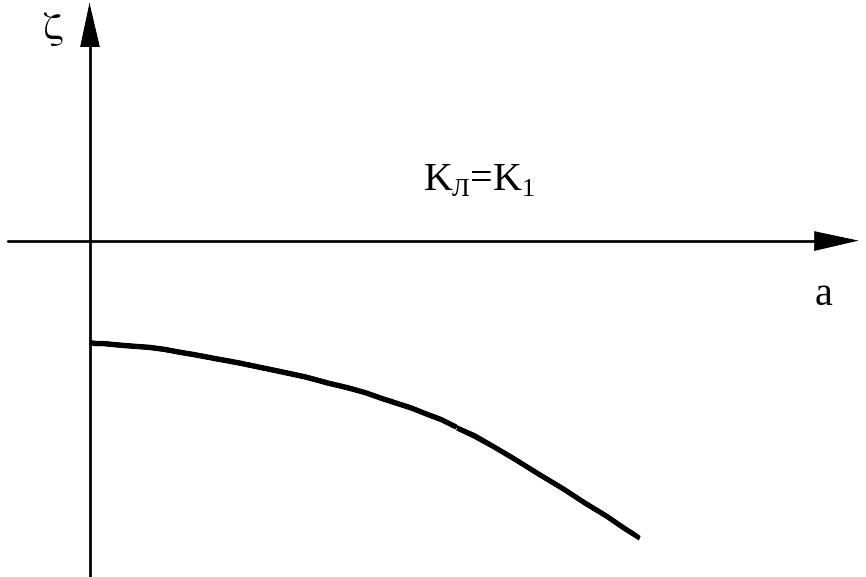
Взяв некоторое значение в об­ласти устойчивости равновесия, получим (идя по вертикали) зависимость , которая имеет вид.

Для значения в области автоколебаний зависимость будет иметь иной вид.

Эти графики дают представление о качестве затухания колебательных переходных процессов при разных значениях параметра .

Можно найти огибающую переходного колебательного процесса согласно (1), по формуле

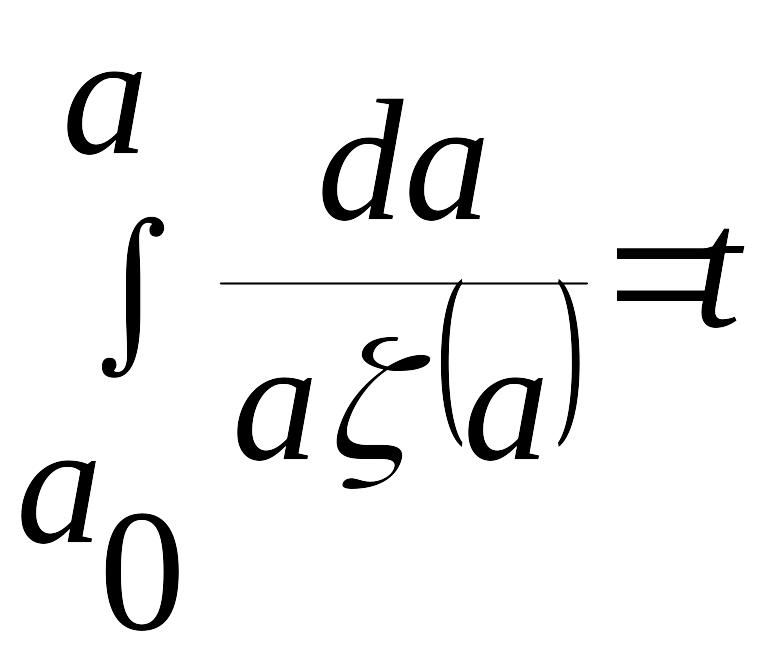. (8)

Интегрирование (8) в конечной форме возможно лишь в простейших случаях. Поэтому приведем графический способ построения огибающей . Введем в рассмотрение текущую «постоянную времени»

.

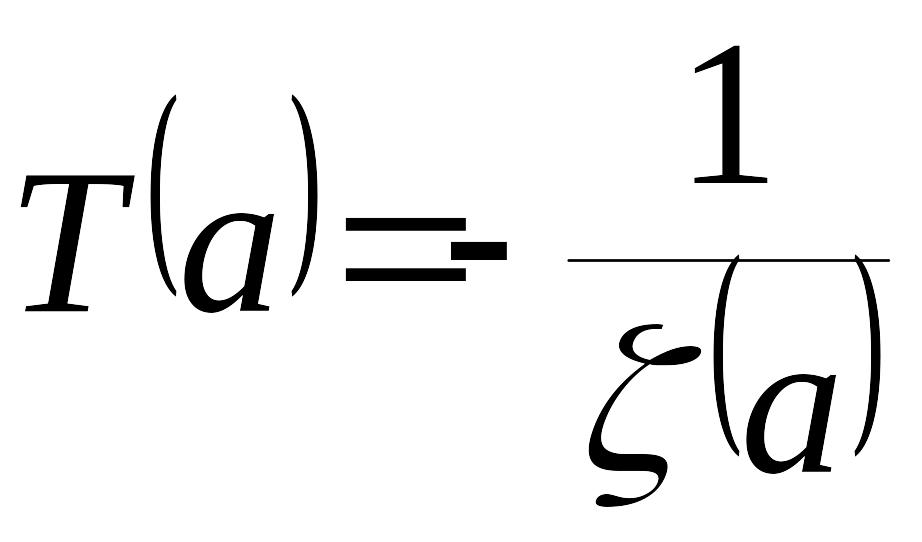В линей­ных системах . Здесь же медленно изменяется с изменением амплитуды. Значения , согласно формуле (9), берутся из диаграммы качества для каждого значения при заданном . Считая на небольшом промежутке времени, проводим графическое построение огибающей указанной на рисунке

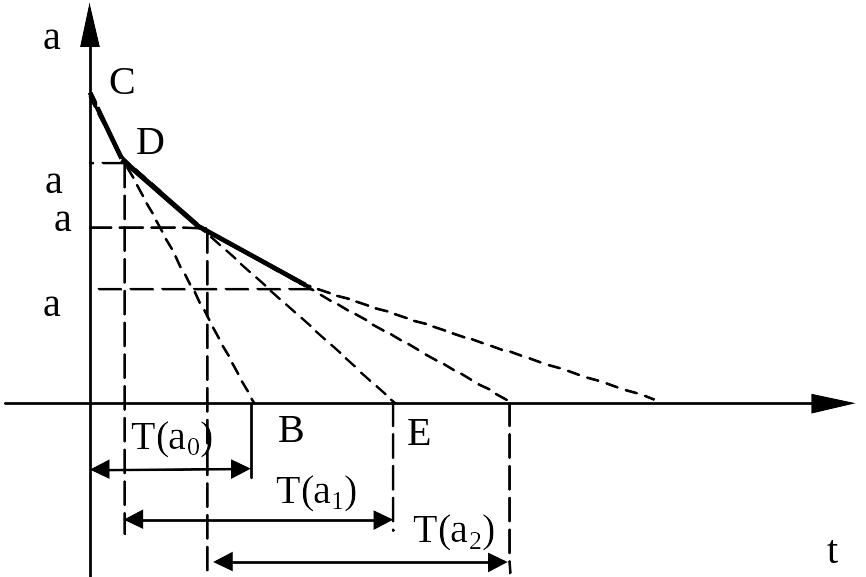
Укажем другой способ оценки быстроты затухания переходных процессов в нелинейной системе с одной однозначной нелинейностью . Передаточная функция линейной части имеет вид

.

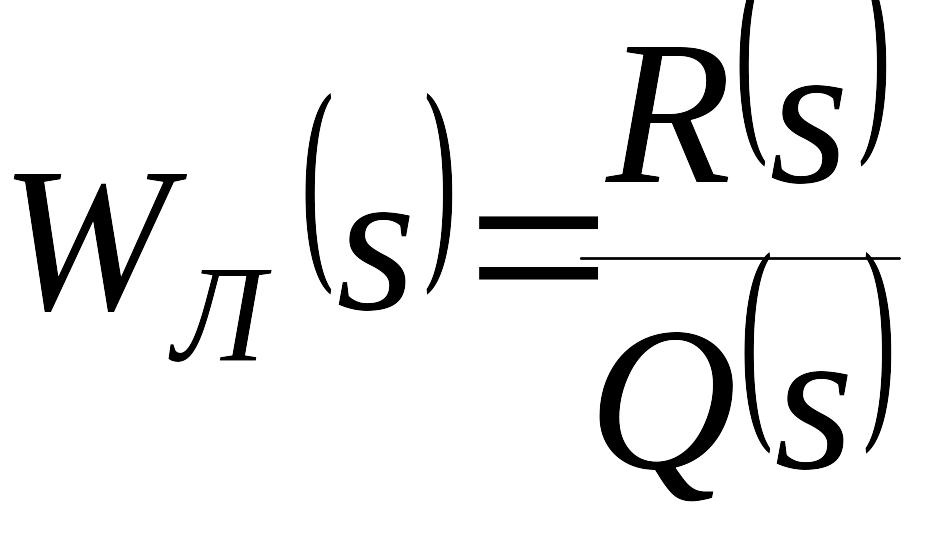Нелинейная характеристика расположена в секторе и может иметь произвольное очертание.

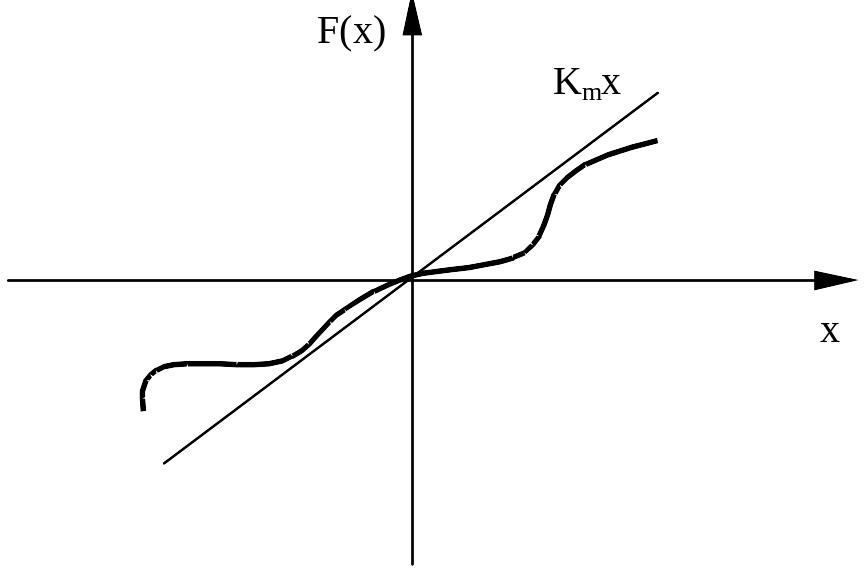
Этот способ основан на применении частотного критерия абсолютной устойчивости.

На комплексной плоскости строится смещенная частотная характеристика, определяемая следующим образом:

(10)

где

.

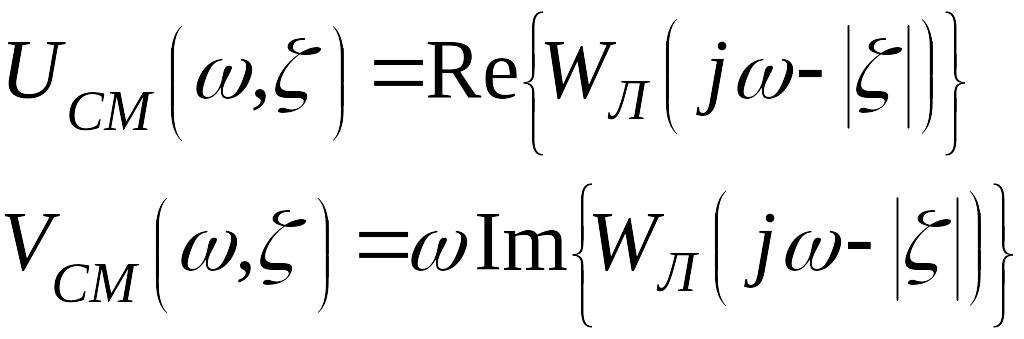Оценить быстроту затухания переходного процесса в системе можно следующим образом.

Нелинейная система с устойчивой линейной частью и нелинейной характеристикой, расположенной внутри сектора , будет обладать показателем затухания, не меньшим данного , если через точку можно провести прямую с любым наклоном так, что она не пересечет смещенной характеристики . Эта оценка проиллюстрирована рисунком

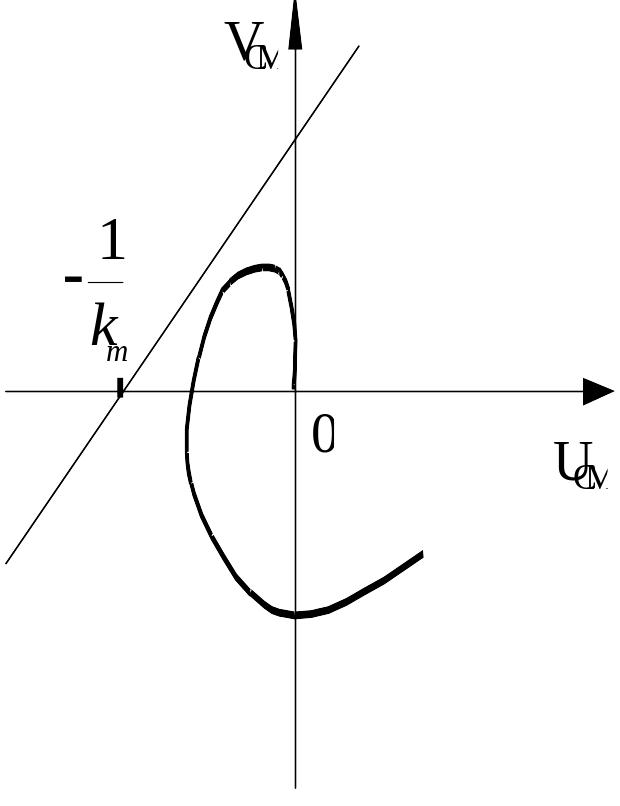
Можно определить предельное значение , при котором в системе имеет место показатель затухания, не меньший , как показано на рисунке.

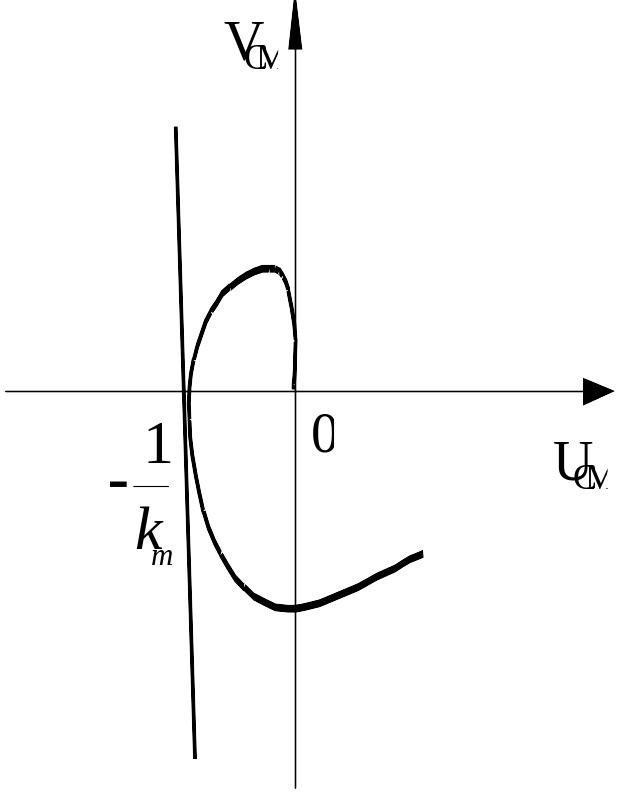
Если построить серию смещенных частотных характеристик для различных значений , то получим зависимость , т.е. зависимость показателя затухания от размера сектора, в котором лежит нелинейная характеристика.

Количественно судить о показателях качества переходного процесса можно непосредственно по диаграммам качества переходного процесса, не строя самого процесса.

Время затухания переходного процесса на заданном интервале изменения амплитуд от до определяется по формуле

.

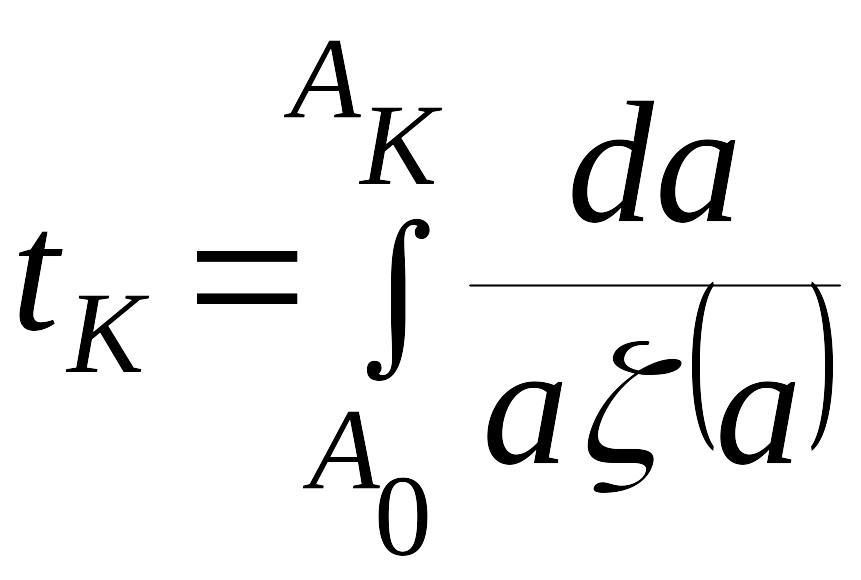На основании чего можно дать приближенную оценку

,

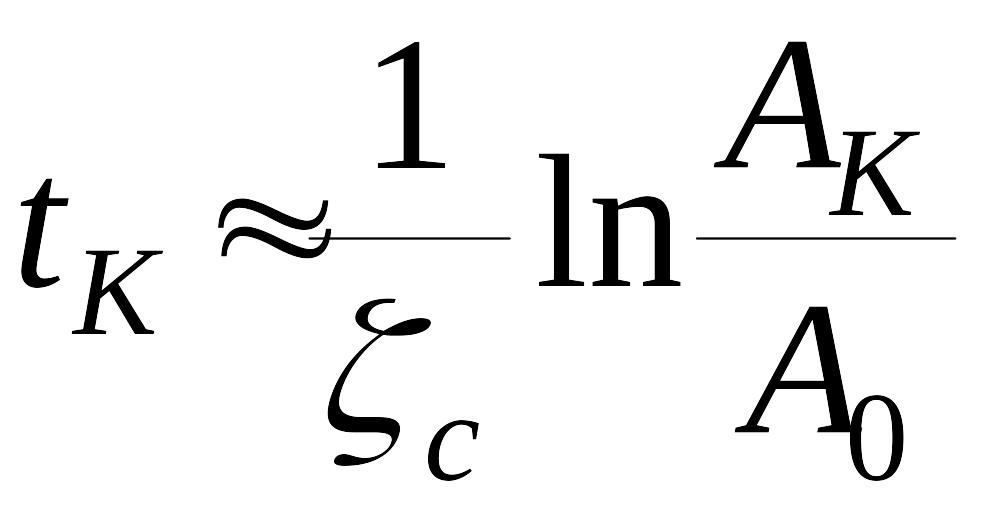где есть среднее значение показателя затухания, взятое ориентировочно из диаграммы качества для исследуемого участка (см. рис.)

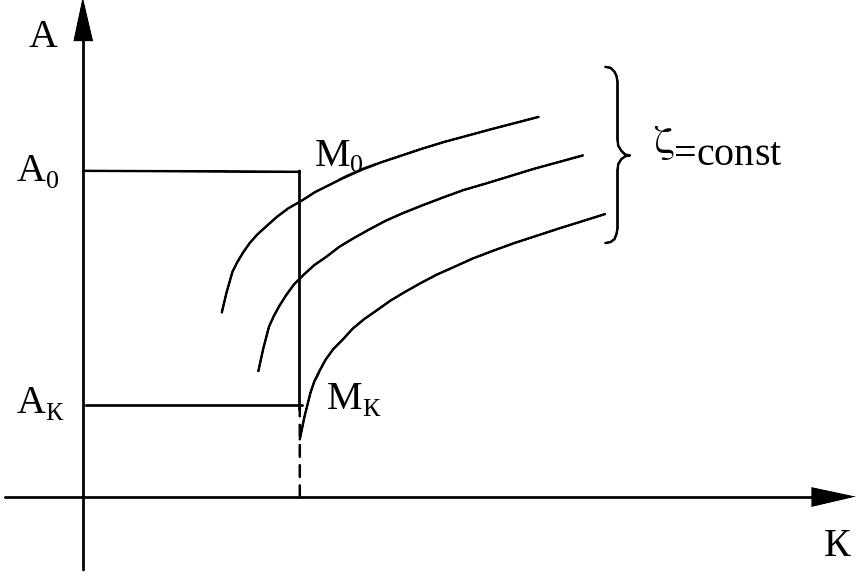
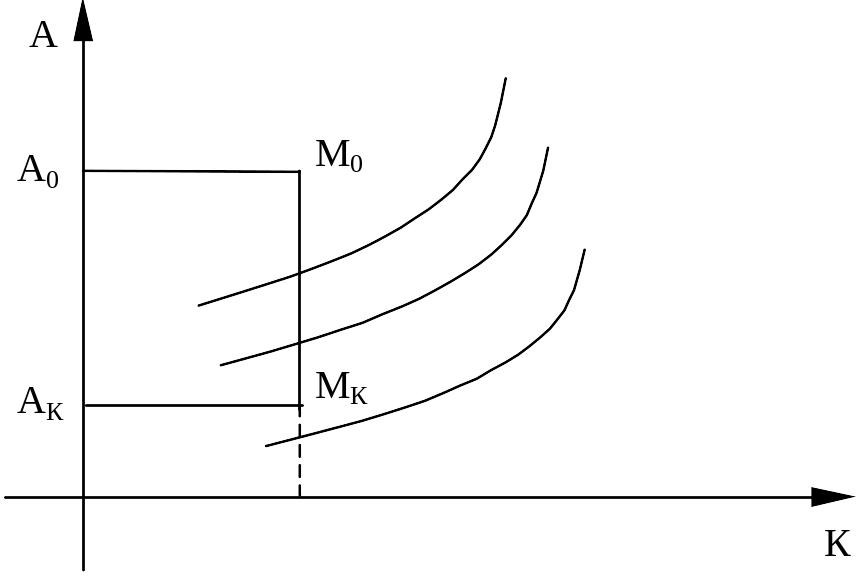
Для более точного определения времени затухания надо разбить участок на отрезков и вычислить

,

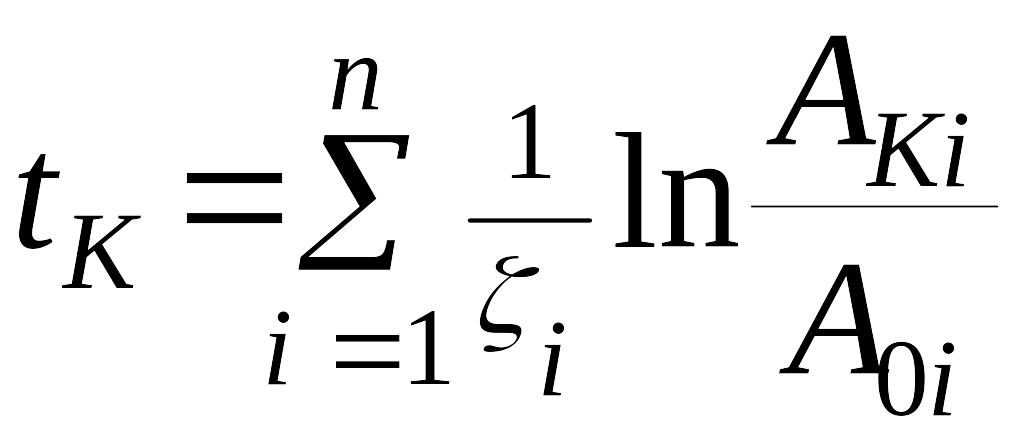где есть взятое из диаграммы значение в середине каждого отрезка ; – значение ординаты в начале и конце каждого отрезка.

Для определения величины перерегулирования надо найти значение амплитуды при

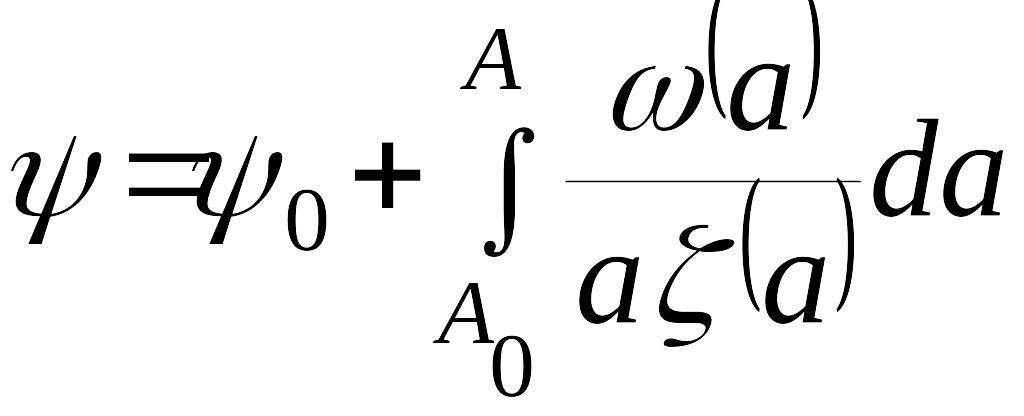
При и приходим к уравнению

,

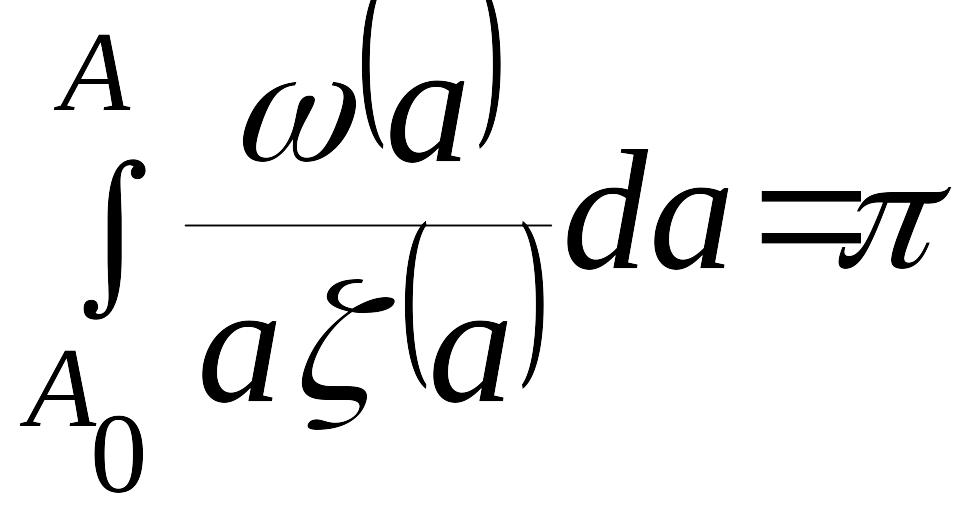откуда можно найти , которое и будет представлять собой величину перерегулирования . В качестве оценки можно использовать

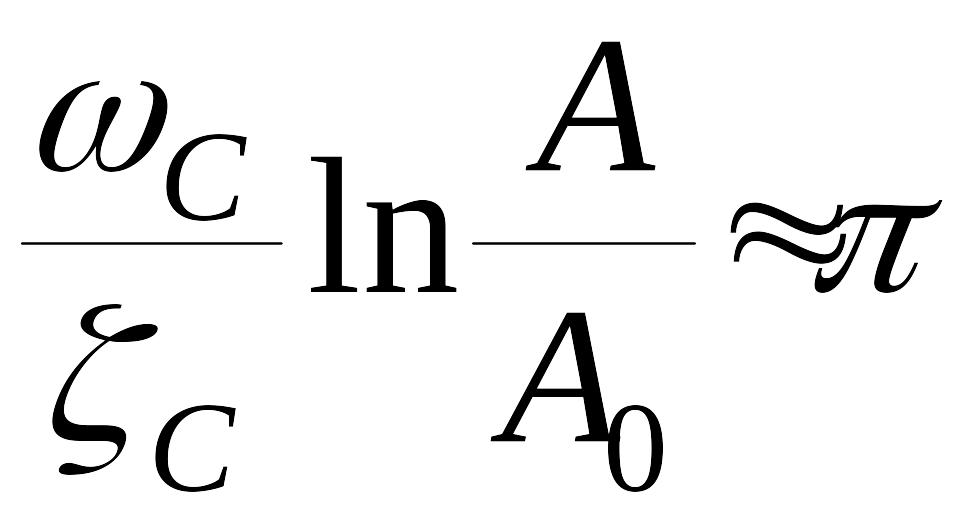, (12)

откуда, учитывая, что получаем оценку перерегулирования в виде

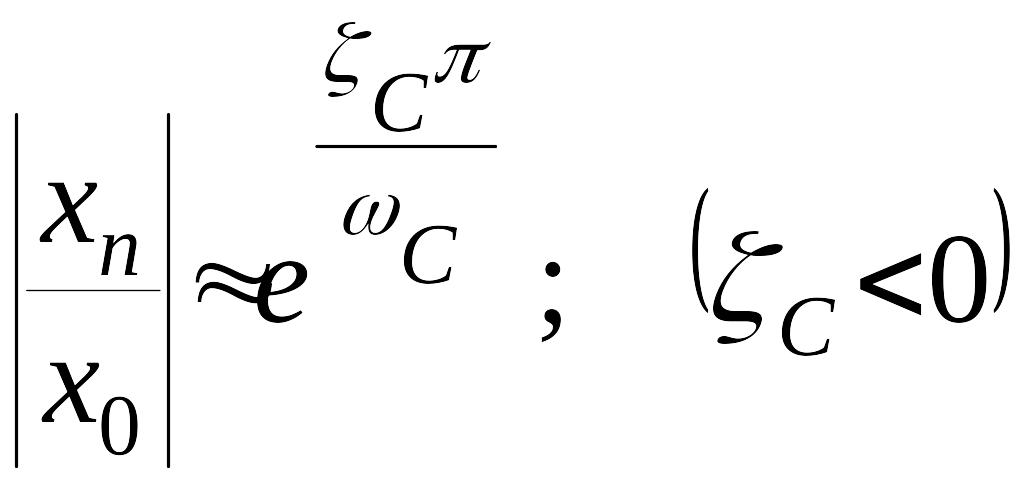, (13)

где и среднее значение величины и взятые из диаграммы для исследуемого участка .

Для более точной оценки величины перерегулирования нужно разбить участок на несколько отрезков и вычислить

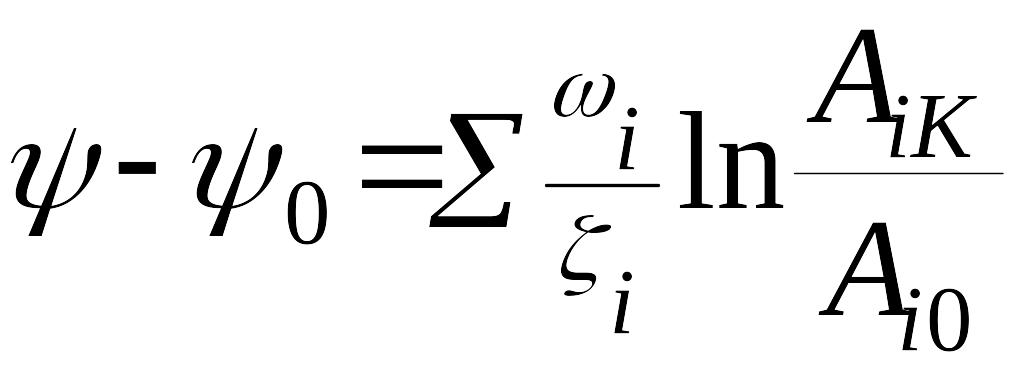, (14)

где и –значения и в середине каждого отрезка; – значение ординаты в начале и конце каждого отрезка.

Вычисления по формуле (14) надо вести, начиная от точки до тех пор, пока не получится в сумме .

При этом величина перерегулирования будет

,

где – ордината конца последнего из отрезов, участвующих в этом вычислении.

Для определения числа колебаний за время переходного процесса надо довести вычисления по формуле (14) до конца, т.е. найти

.

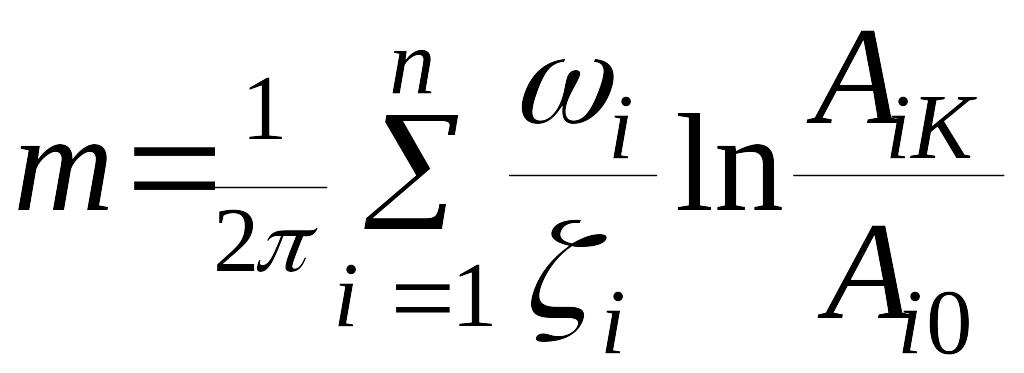Для грубой оценки можно считать

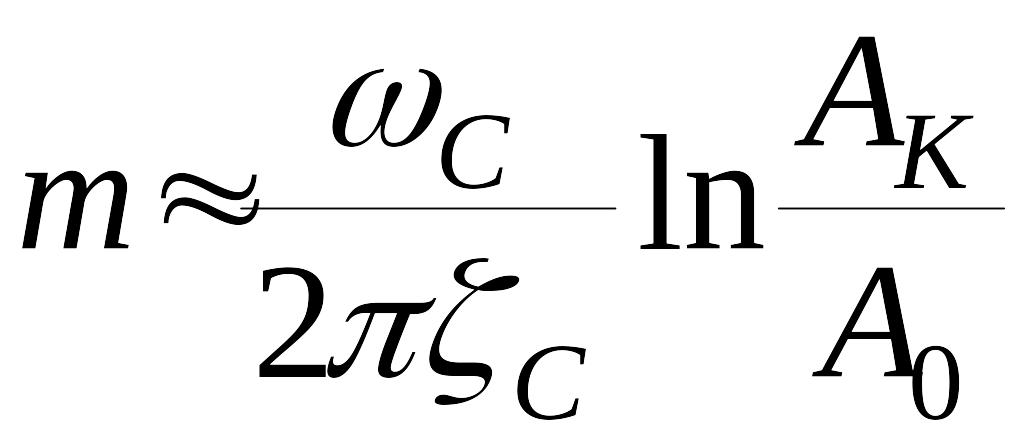
Если, например, требуется, чтобы на исследуемом отрезке было не более одного колебания, то надо потребовать, чтобы

.

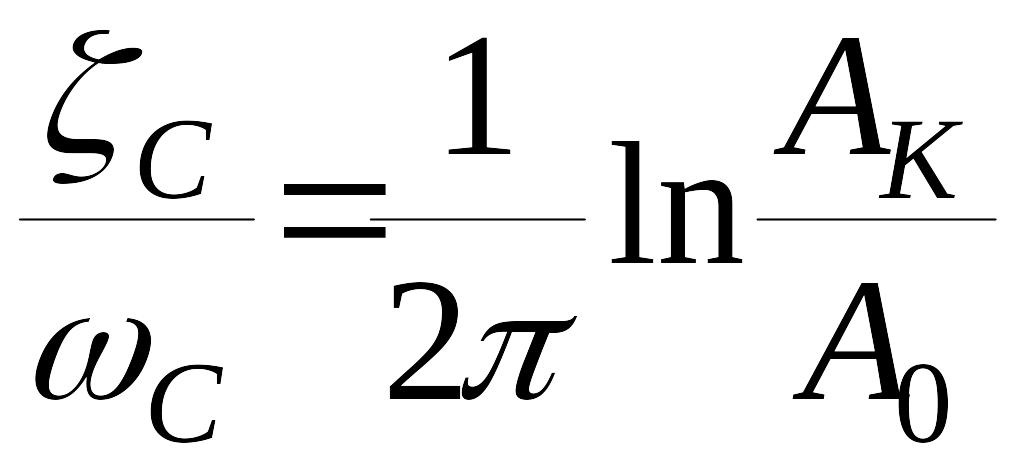Если же задано максимально допустимое перерегулирование , то, согласно (9), должно быть

.

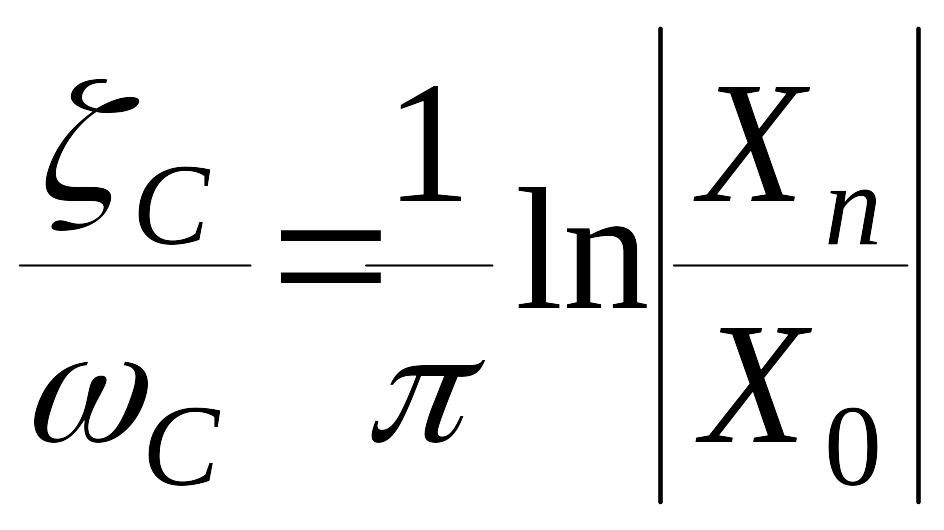Диаграммы качества строятся для переменной , стоящей в уравнении системы под знаком нелинейности. Если желательно пересчитать ее на какую-либо другую переменную, то можно применить формулу для определения амплитуды новой переменной, используя соответствующую передаточную функцию, связывающую эти переменные в исследуемой системе.

3.ЛАБОРАТОРНЫЕ ЗАНЯТИЯ