Видоизмененная частотная характеристика.

Выше при помощи соотношения (14) была выведена функция

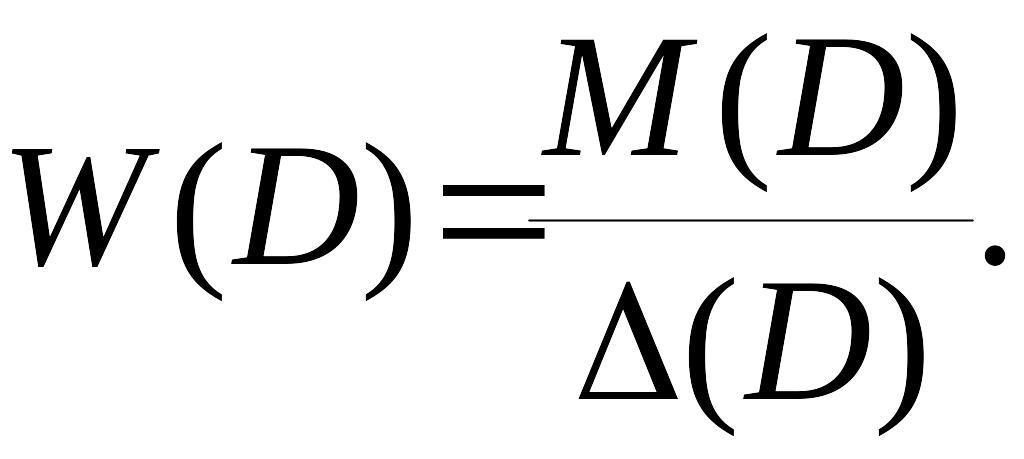
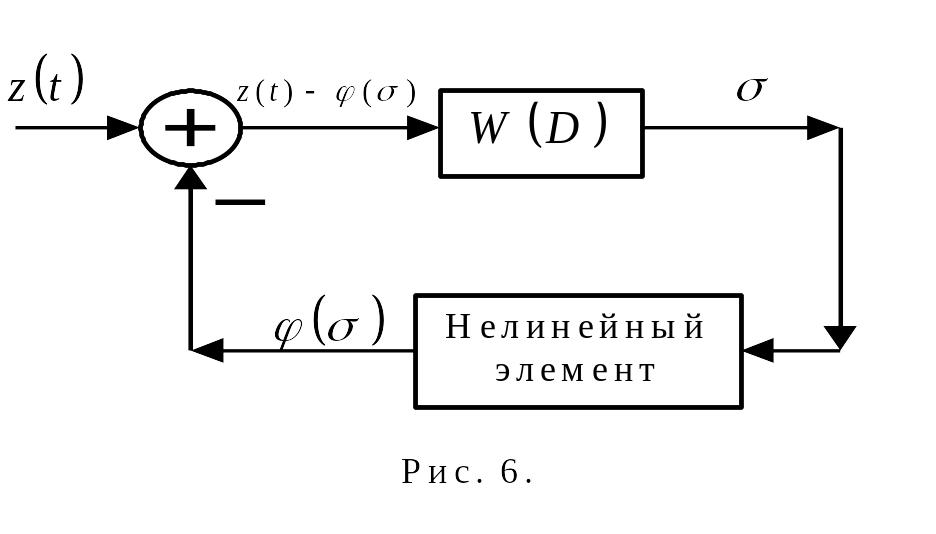
Разомкнем цепь обратной связи у системы, изображённой на рис.2. Разомкнутая система (рис.6) будет описываться уравнением

, (25)

где через обозначен сигнал, поданный на вход системы.

Как следует из уравнения (25), функция представляет собой передаточную функцию разомкнутой системы, показанной на рис.6. В соответствии с выражением (14) частотная характеристика разомкнутой системы будет

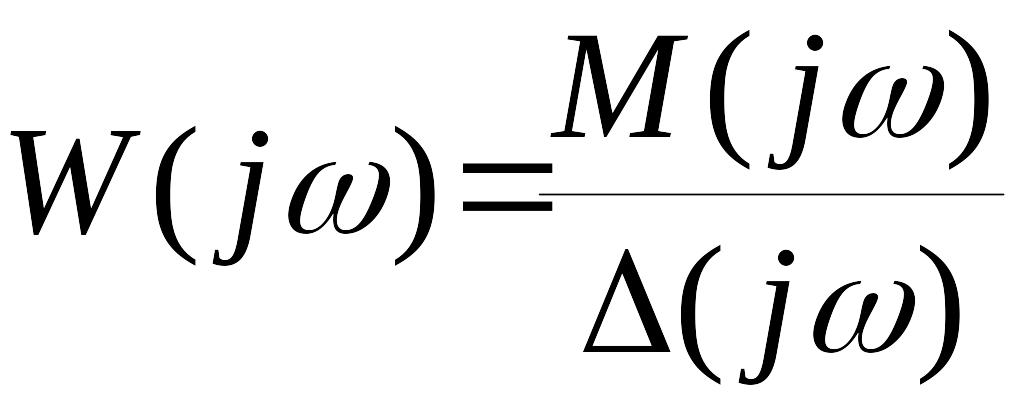. (26)

Введём теперь функцию , определяемую следующими соотношениями

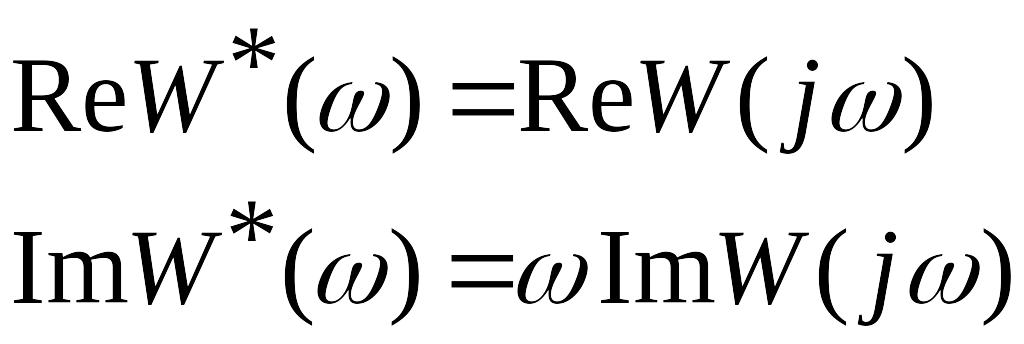, (27)

Таким образом, функция будет иметь вид

. (28)

Так как является четной функцией от , а является нечетной функцией от , то в соответствии с (27) функция будет четной функцией от и, таким образом,

. (29)

Функция называется видоизменённой частотной характеристикой.

Так как в соответствии с (14) функция представляет собой дробно-рациональную функцию, степень числителя у которой ниже степени знаменателя, то для будем иметь следующее выражение

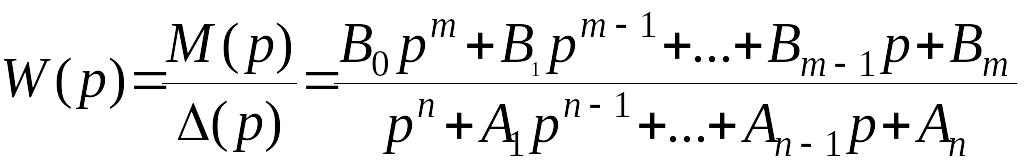, . (30)

В знаменателе выражения (30) коэффициент при равен единице, так как согласно (9) . Полагая , получим согласно (30), что

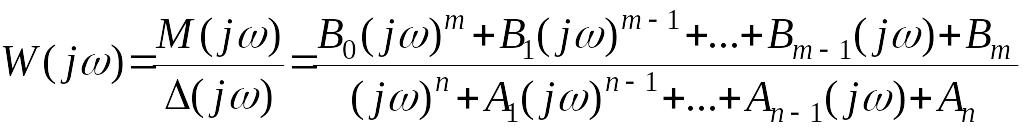. (31)

Из выражения (31) следует, что

, . (32)

Умножая левую и правую части выражения (31) на , получим

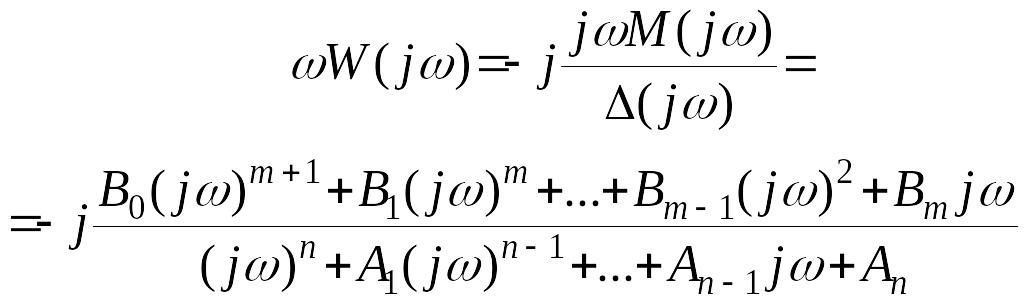. (33)

Учитывая, что в соответствии с (27)

,

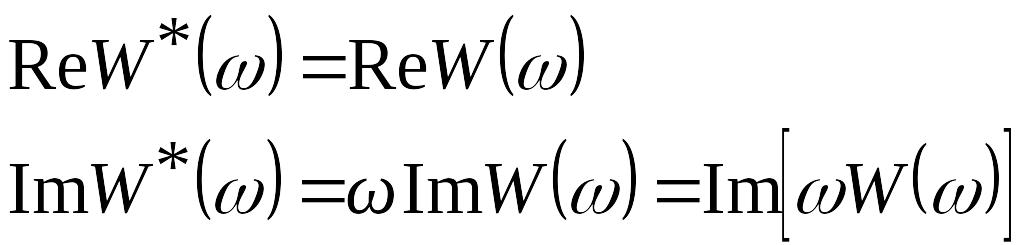найдем, что

, ,

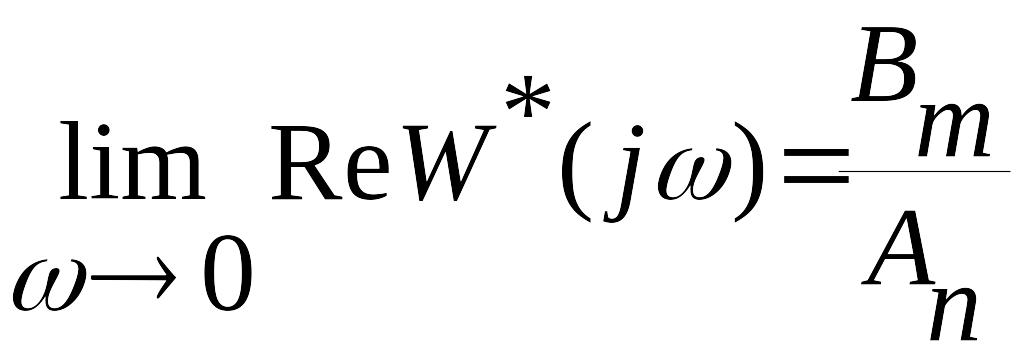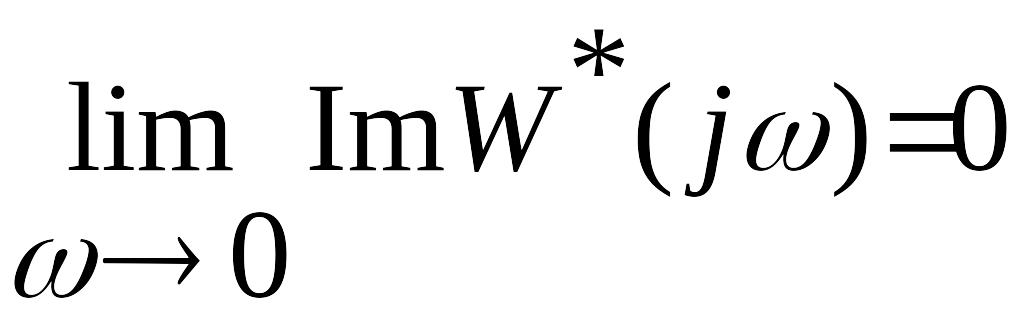и, следовательно

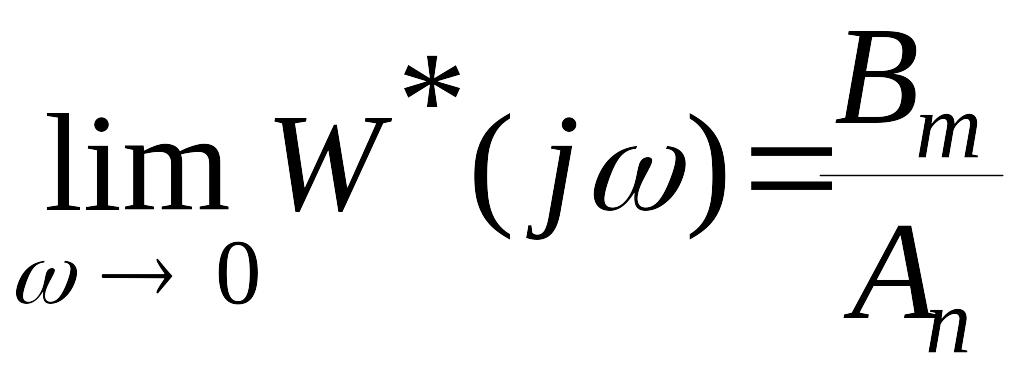. (34)

Значение 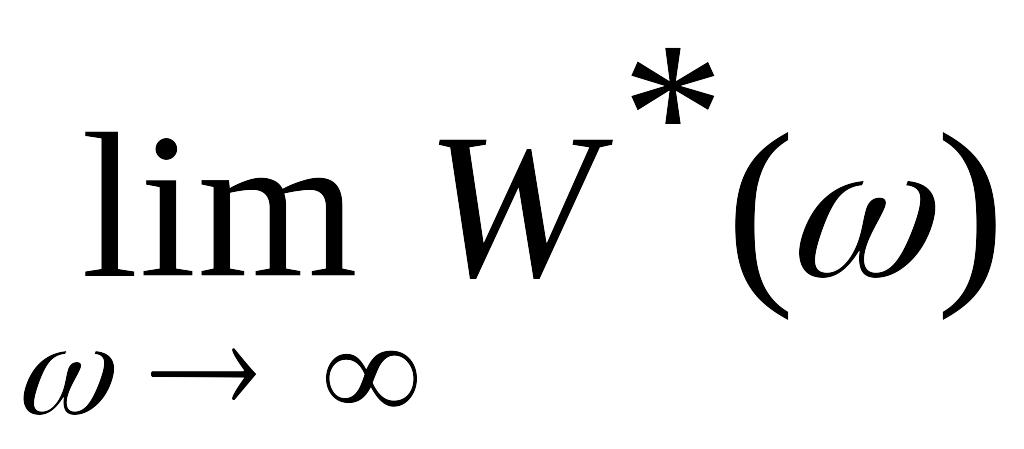будет различным в случае, когда , и в случае, когда .

При , то есть при , будем согласно (31) и (33) иметь

, .

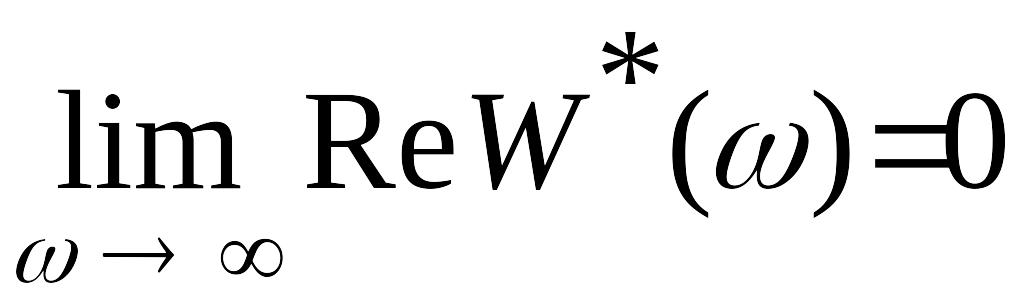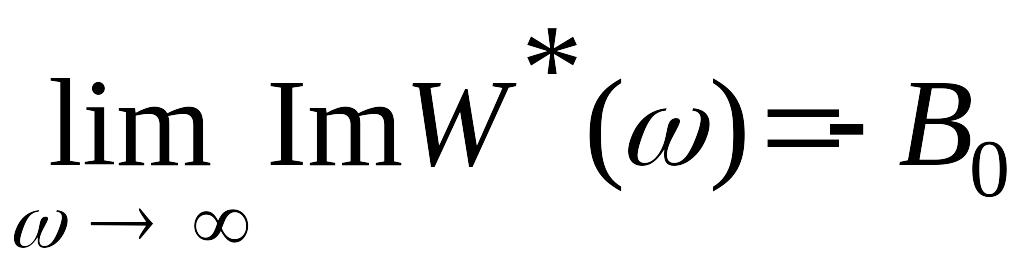При будем иметь

, .

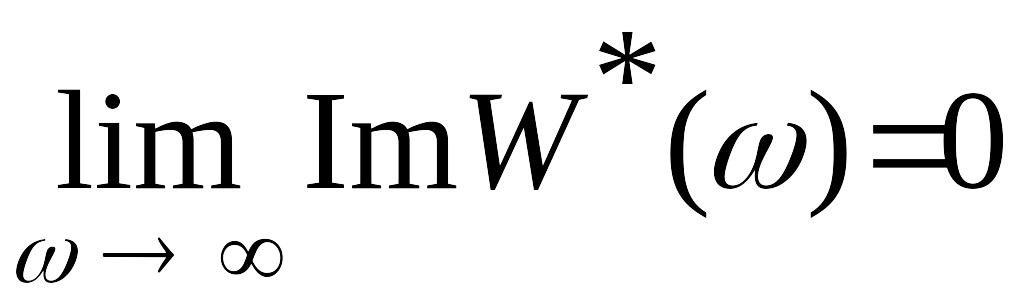Таким образом,

.

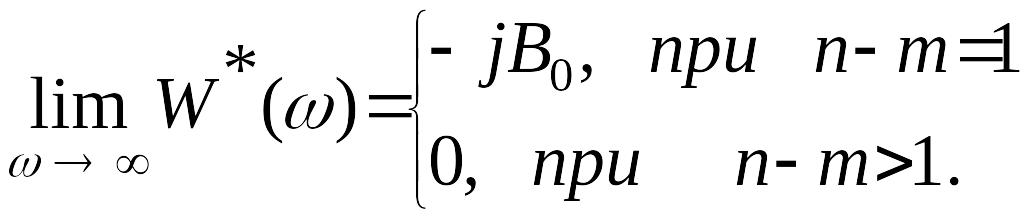Критерий устойчивости В. М. Попова.

Определение. Систему (1)

, ,

, (1)

,

тривиальное решение которой асимптотически устойчиво при любых видах функции , удовлетворяющих условию (6)

,

будем называть абсолютно устойчивой в угле .

Так как линейные функции , входят в число допустимых условием (6) функции , то требование, чтобы годограф вектора не пересекал полуотрезка (рис. 5), является необходимым условием абсолютной устойчивости системы (1). Достаточное условие абсолютной устойчивости даёт теорема В.-М. Попова.

Критерий устойчивости В.-М. Попова. Для того чтобы система (1) была абсолютно устойчива в угле , достаточно, чтобы существовало такое конечное действительное число , при котором для всех значений выполнялось условие

. (36)

Заметим, что сформулированное в теореме В.-М. Попова достаточное условие (36) абсолютной устойчивости нелинейной системы существенно отличается от требований критерия Найквиста для линейных систем. Последний накладывает ограничение на значение лишь в точках, где . В других точках значение может быть любым, так как ограничение значения в точках, где , уже предотвращает возможность охвата точки годографом вектора , что и обеспечивает асимптотическую устойчивость замкнутой линейной системы. Сформулированное же в теореме В.-М. Попова достаточное условие (36) абсолютной устойчивости нелинейной системы требует ограничения значений для всех , а не только в точках, где .

Выше была введена видоизменённая частотная характеристика . Обозначим через и соответственно действительную и мнимую части . Согласно (27) будем тогда иметь

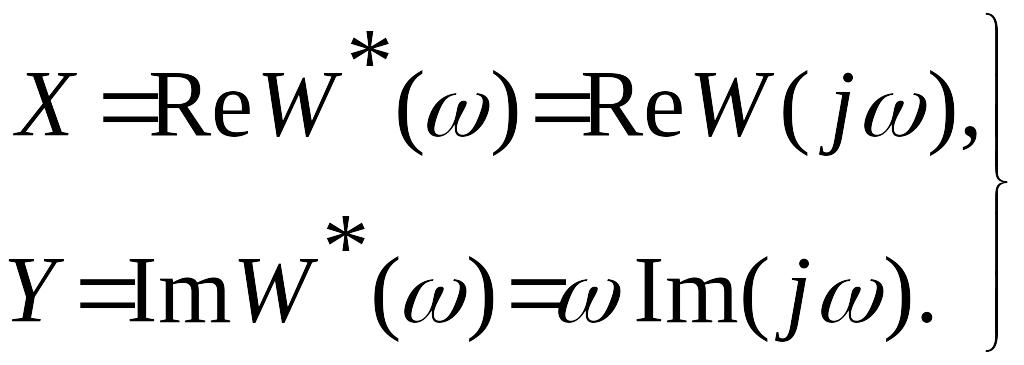(37)

В соответствии с (37)

(1.38)

Условие (36), таким образом, принимает вид

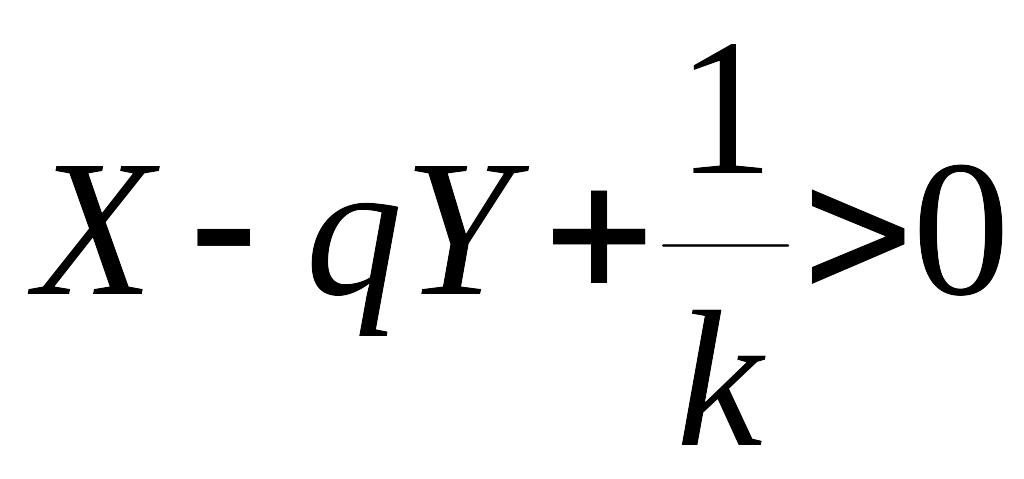(для всех ). (39)

На плоскости (то есть на плоскости комплексного переменного ) уравнение

,

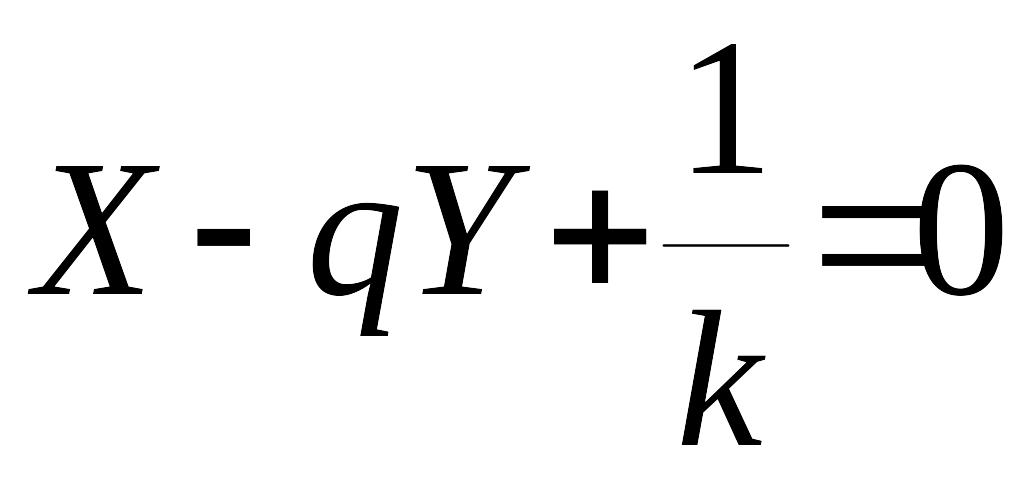или эквивалентное ему уравнение

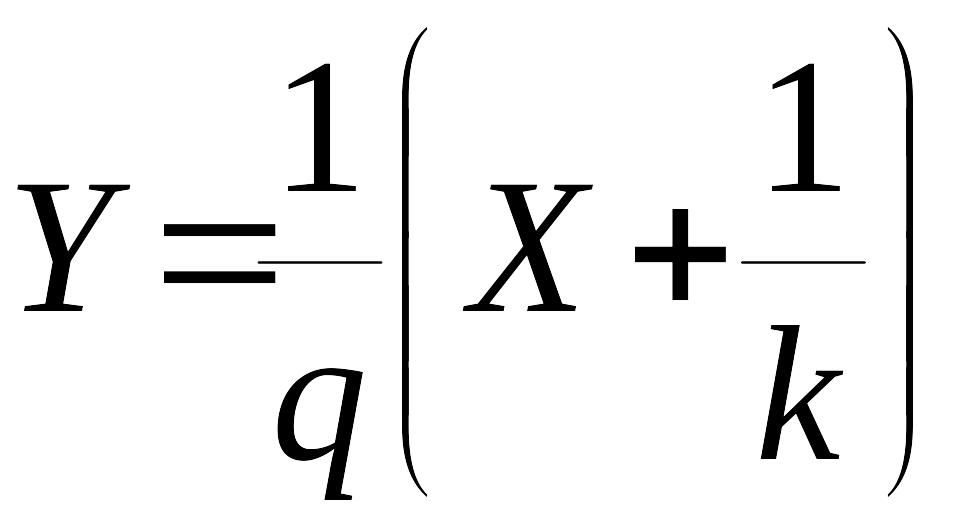, (40)

определяет собой прямую (рис.7), проходящую через точку . Угловой коэффициент этой прямой равен . Прямую (40) можно назвать прямой Попова.

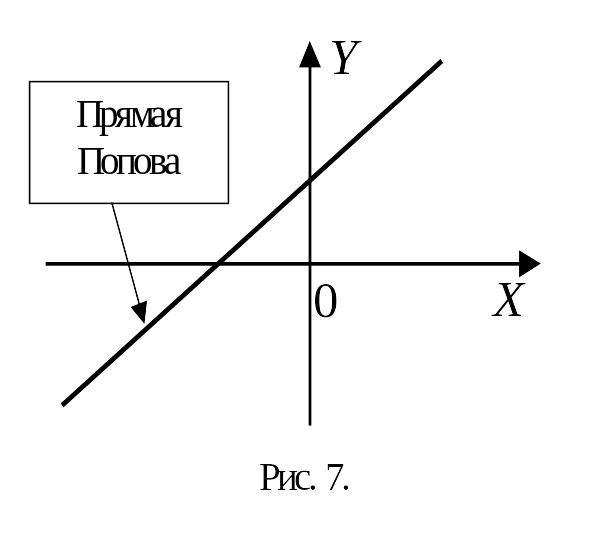
Нетрудно видеть, что условие (39) выполняется в любой точке плоскости комплексного переменного ,расположенной правее прямой Попова. Иными словами, условие (39) означает, что годограф вектора должен быть расположен правее прямой Попова.

Итак, если в системе имеется нелинейный элемент с однозначной характеристикой (см. рис. 8), то возможны два случая. Первый – нелинейная характеристика расположена в секторе (см. рис. 8), второй в секторе .

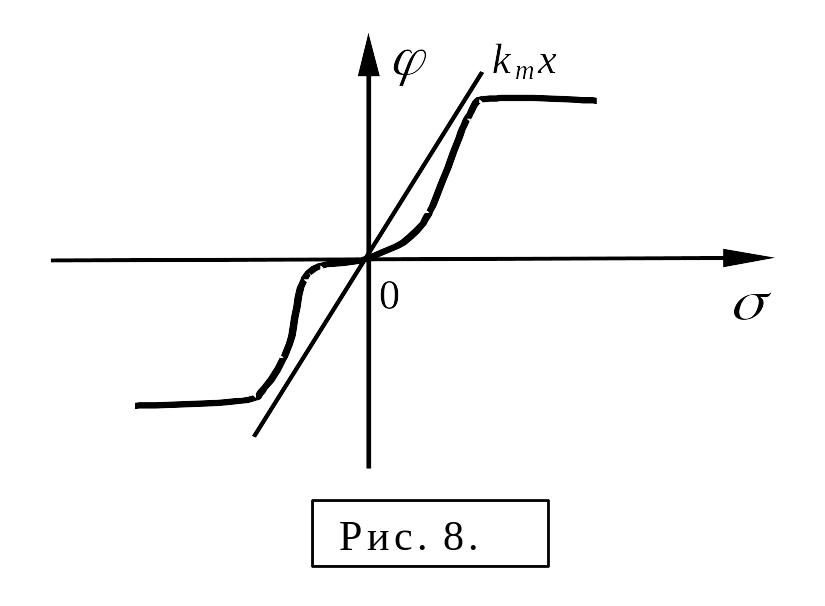
Начнем с первого случая,

. (41)

Пусть теперь линейная часть системы описывается уравнением , причем степень многочлена больше степени многочлена .

Передаточная функция линейной части 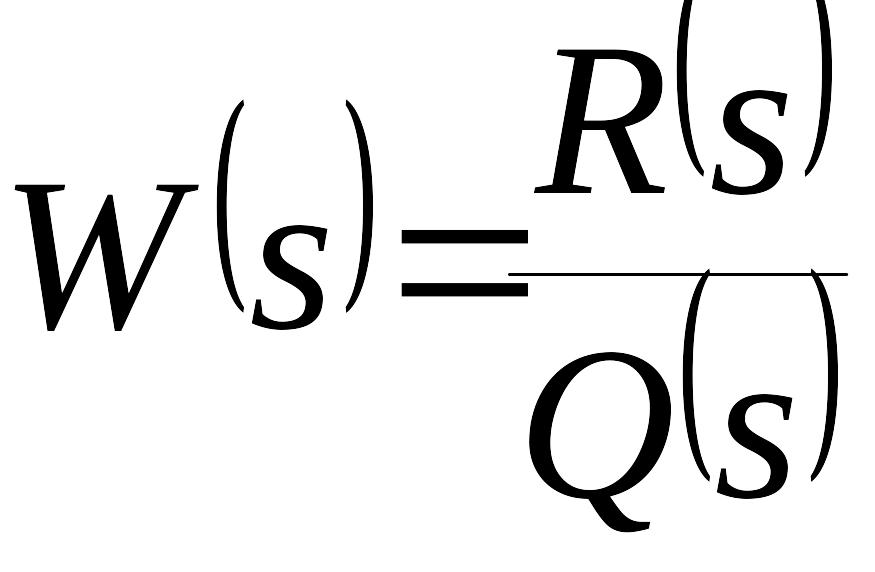имеет полюса с отрицательными вещественными частями, причем допускается наличие не более двух нулевых полюсов.

По критерию В.М. Попова состояние равновесия нелинейной системы будет абсолютно устойчивым, если нелинейная характеристика находится в секторе и существует такое действительное число , что при всех выполняется неравенство

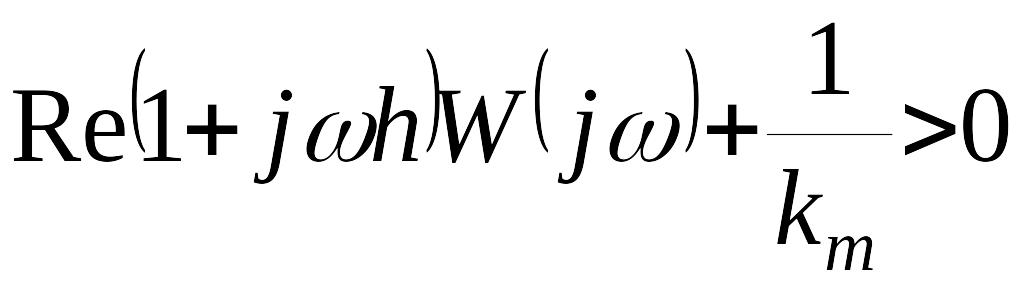, (42)

где – амплитудно-фазовая частотная характеристика линейной части системы.

Для удобства графического представления этого критерия вводится модифицированная частотная характеристика линейной части

,

где

. (43)

Следовательно график имеет вид, аналогичный амплитудно-фазовой характеристики линейной части и отличается от нее только масштабом по мнимой оси (рис. 9).

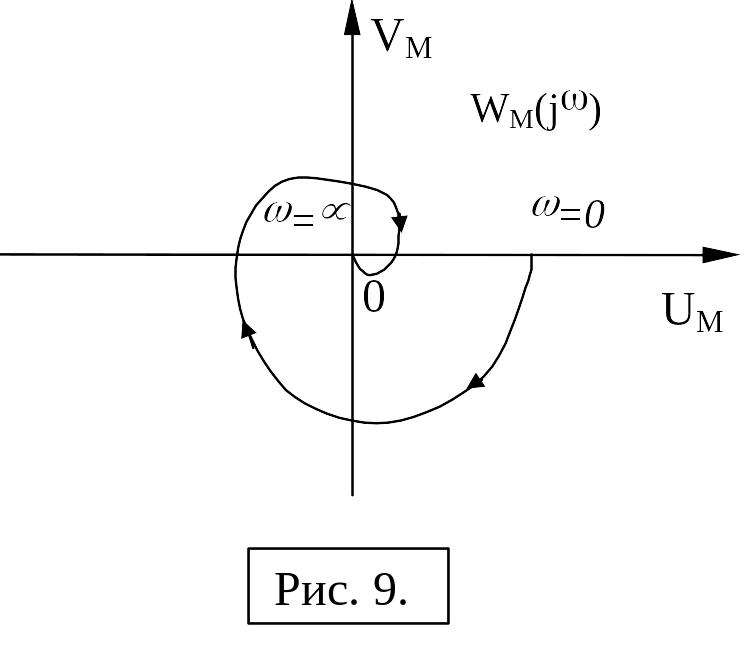
Поскольку выражение (42) можно записать в виде

,

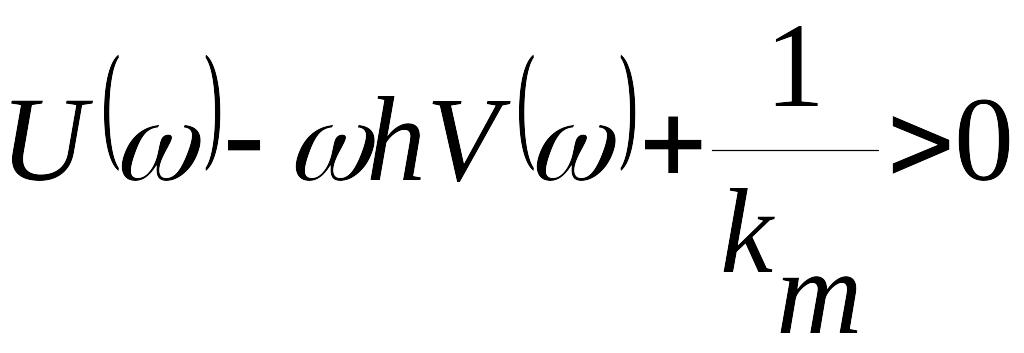то с подстановкой (43) оно преобразуется к виду

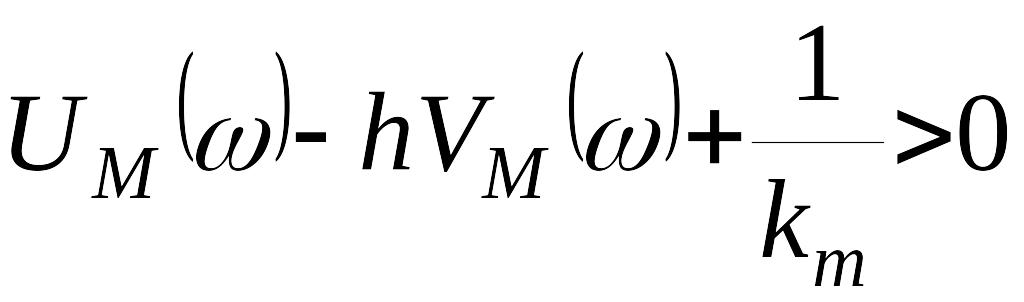. (44)

Выражение

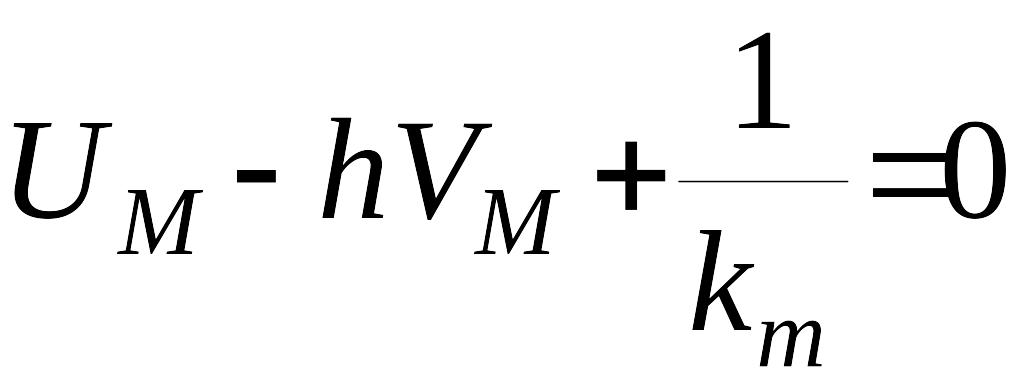(45)

представляет собой уравнение прямой на плоскости прямоугольных координат . Эта прямая проходит через точку на оси и имеет крутизну наклона .

Отсюда вытекает следующая формулировка критерия абсолютной устойчивости.

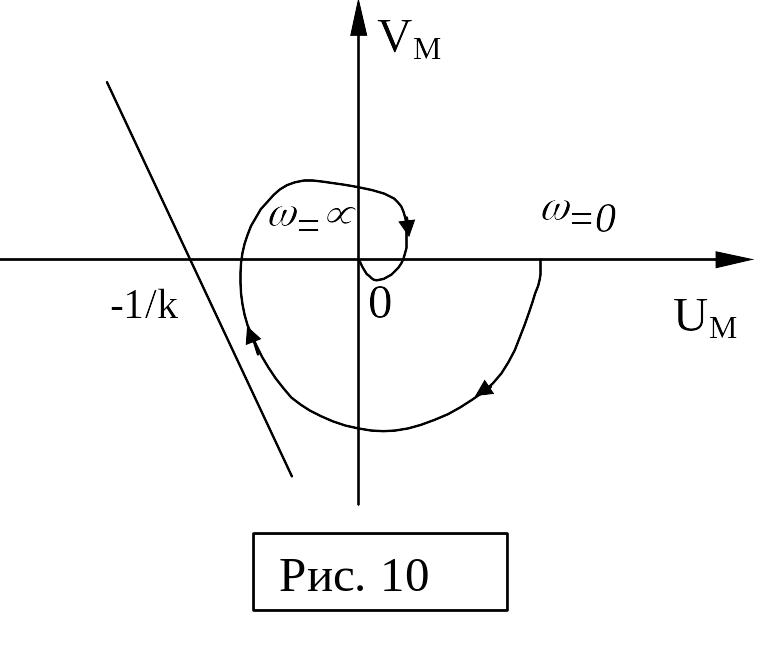
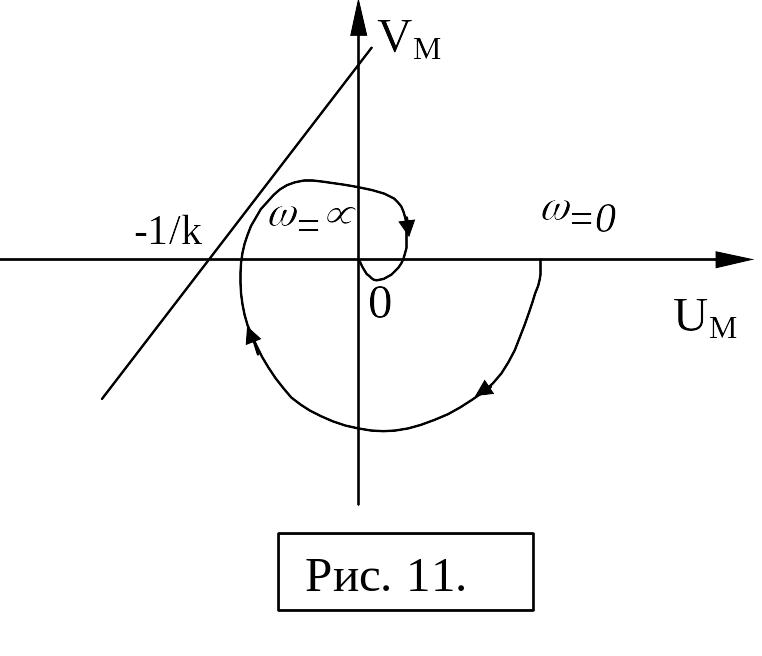
Состояние равновесия нелинейной системы абсолютно устойчиво, если нелинейная характеристика находится внутри сектора и можно провести через точку прямую так, что она не пересечет модифицированную частотную характеристику (последняя лежит справа).

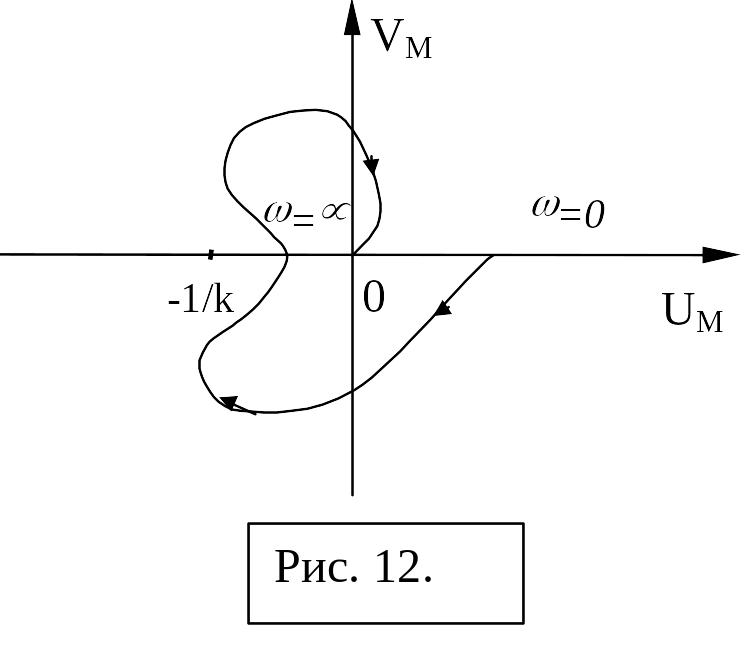
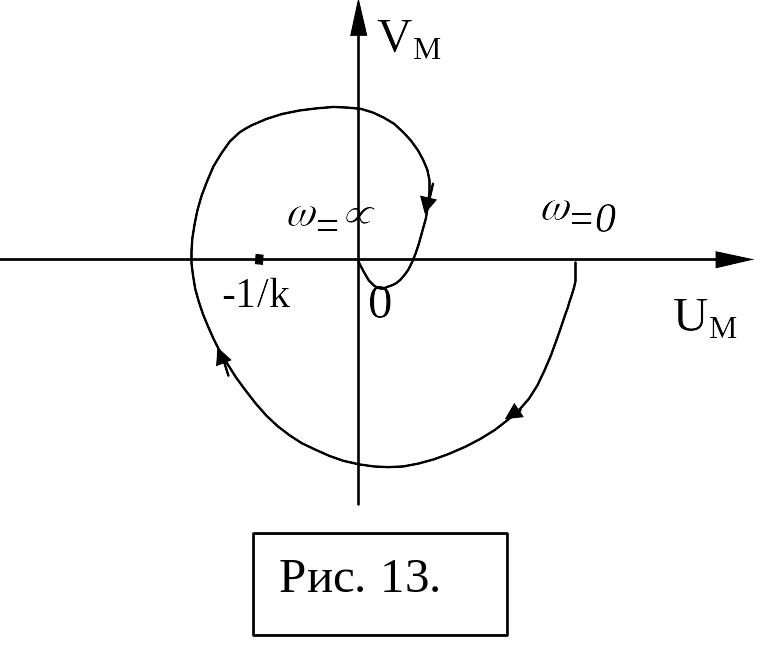
На рис. 10 и 11 показаны случаи, когда критерий абсолютной устойчивости выполняется, а на рис. 12 и 13 – не выполняется.

ЛЕКЦИЯ 15. ОЦЕНКА КАЧЕСТВА ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.

Рассмотрим определение качества переходных колебательных процессов в нелинейных системах.

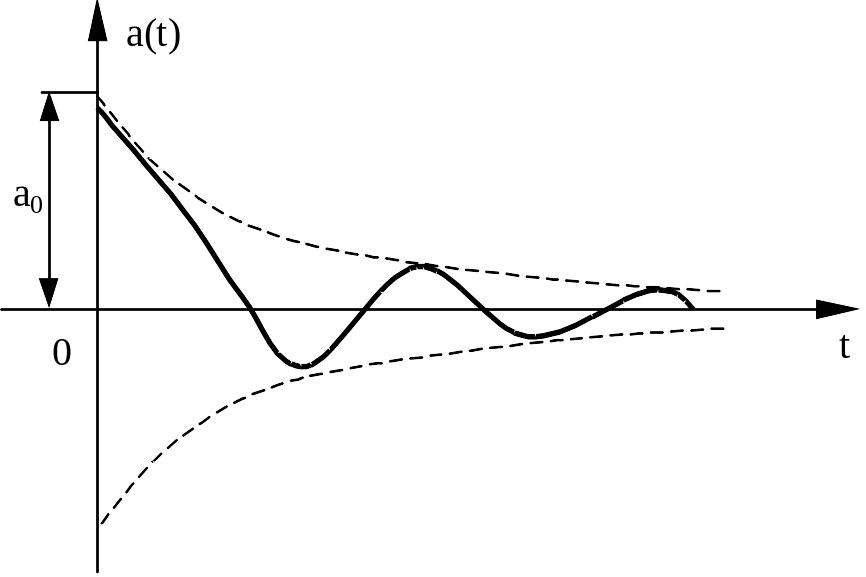
Эти процессы могут быть

1. затухающими (к нулю либо к автоколебаниям);

2. расходящимися (изнутри до амплитуды автоколебаний; неограниченно возрастающие неустойчивые процессы).

Колебательные переходные процессы в системе управления будем рассматривать как собственные колебания при отсутствии внешних воздействий во время самого процесса.

Рассмотрим систему, структурная схема которой может быть приведена к виду

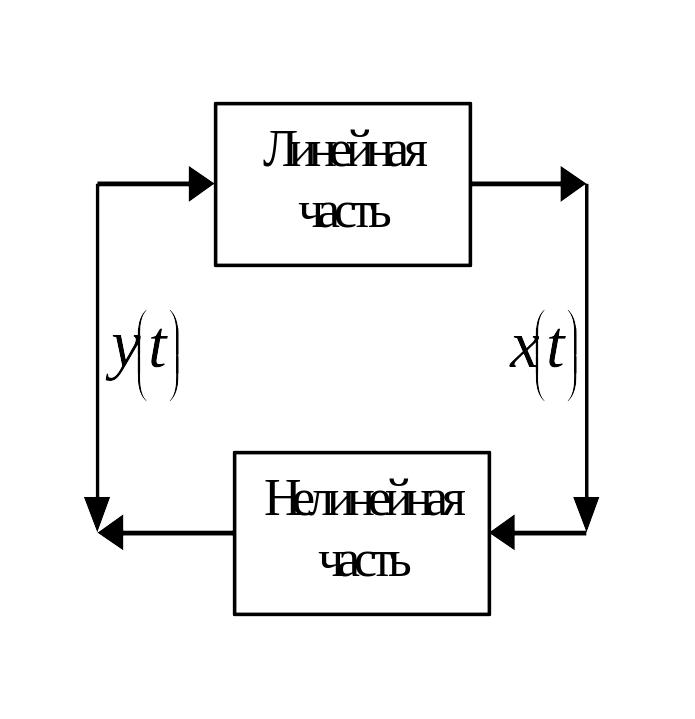
Будем считать, что динамика замкнутой системы описывается уравнением

. (1)

В линейных системах синусоидальные переходные процессы имеют вид

. (2)

Для линейной системы высокого порядка такое решение является приближенным в том смысле, что оно соответствует одной паре комплексных корней характеристического уравне­ния системы. Чтобы это решение отвечало основной части переходного процесса, эта пара корней должна быть ближайшей к мнимой оси.

В нелинейных системах, удовлетворяющих свойству фильтра, будем считать, что переходные колеба­тельные процессы близкими к синусоидальным (2), полагая, что показатель затухания и частота изме­няются медленно с изменением амплитуды колебаний в ходе процесса. Сама же амплитуда изменяется быстро.

Тогда решение вместо (2) надо искать в виде

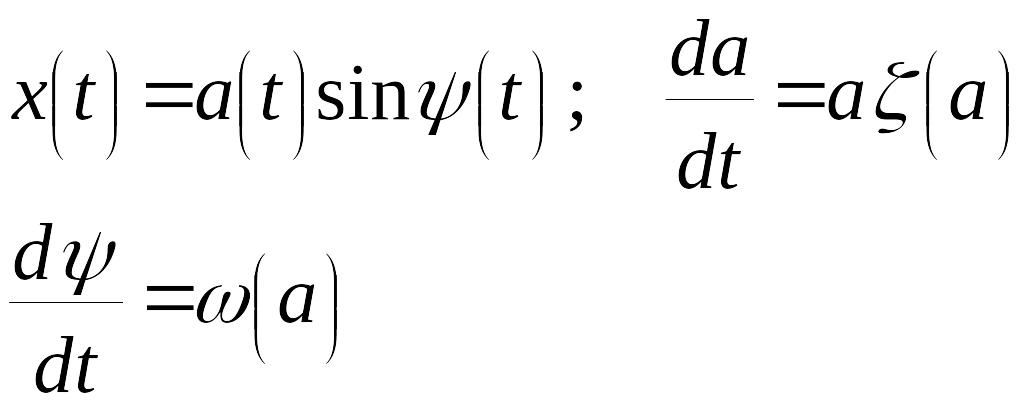. (3)

(как частный случай получается формула (2) для линейной системы)

При колебания затухают,

При – расходятся.

Гармоническая линеаризация нелинейного звена здесь изменится, т.к. из (3) следует

.

Отсюда

.

Поэтому первая гармоника колебаний на выходе нелинейного звена имеет вид

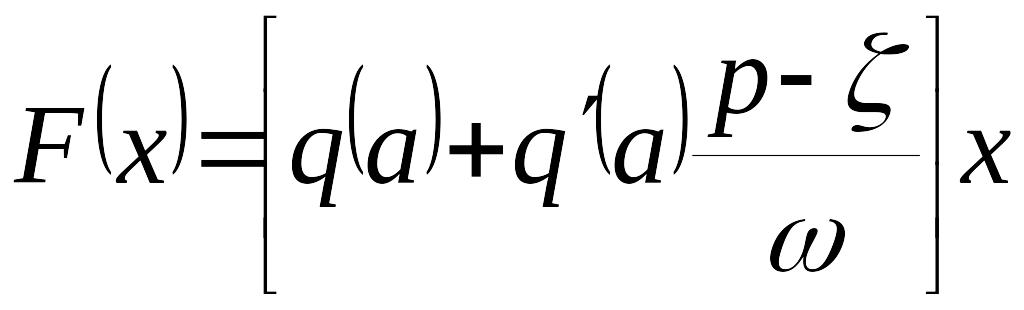, (4)

где коэффициенты гармонической линеаризации и вычисляются по формулам

,

.

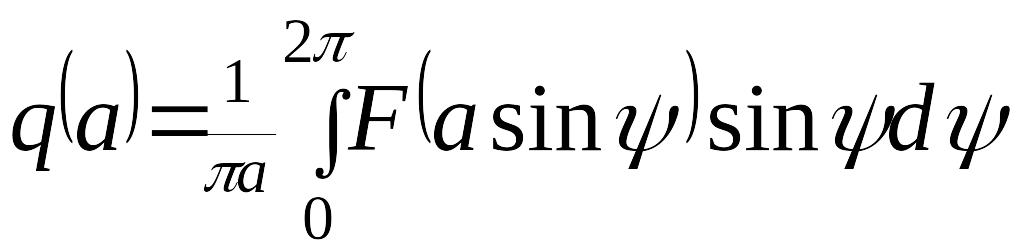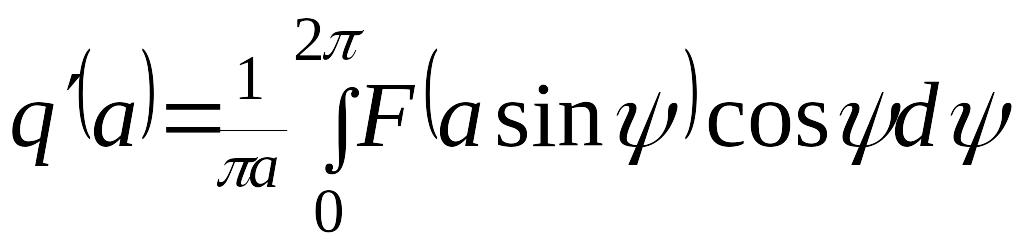Колебательные процессы в линейных системах соответствуют комплексно сопряженные корни характери­стического уравнения системы. Следовательно, для их определения нужно в характеристическое уравнение гармонически линеаризованной системы

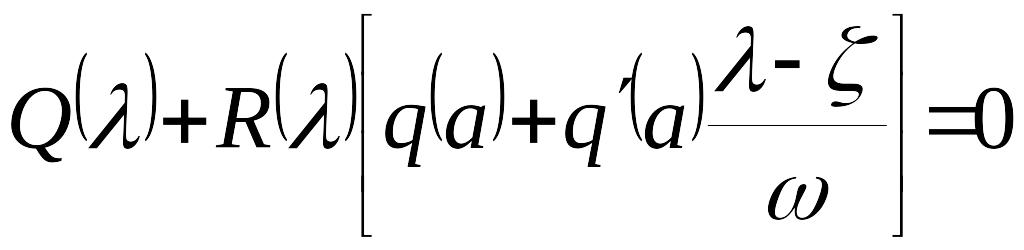
подставить , полагая, что это соответствует ближайшей к мнимой оси паре комплексных корней. В результате получим

. (5)

Это уравнение относительно трех неизвестных: . Следовательно, из этого уравнения можно найти, например,

. (6)

Этого достаточно, чтобы затем по формулам (3) приблизительно определить и кривую переходных колебаний .

В большинстве случаев при проектировании системы автоматического управления и регулирования не требуется вычислять кривую переходного процесса. Нужна лишь оценка быстроты затухания и частоты колебаний, т. е. для оценки качества переходного процесса в колебательных нелинейных системах в большинстве случаев можно ограничиться определением зависимостей из уравнения (5).

Один из способов определения этих зависимостей состоит в следующем. Выделим в уравнении (5) вещественную и мнимую части и получим два уравнения

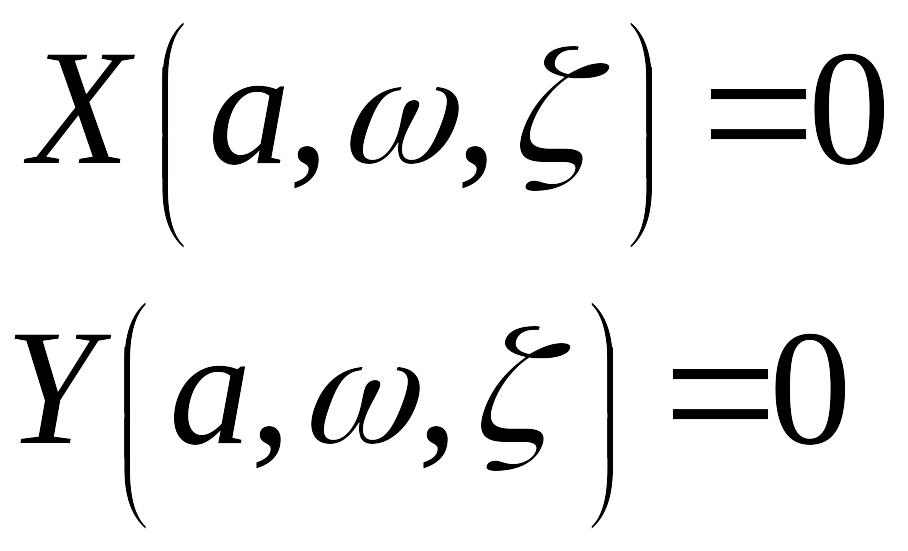, (7)

из которых и определяется зависимость (6).

Если требуется выбрать какой-либо параметр системы, например коэффициент усиления линейной части , так, чтобы и удовлетворяли заданным требованиям, то можно пользоваться так называемыми диаграммами качества.