Теоремы Ляпунова.

Различают теоремы первого и второго методов Ляпунова. Теоремы первого метода Ляпунова использовались при исследований устойчивости линеаризованных систем. Здесь пойдет речь о теоремах второго или, как иногда называют, прямого метода Ляпунова.

Теорема Ляпунова об устойчивости. Она формулируется следующим образом. Если для системы уравнений (6) существует знакоопределенная функция , производная которой 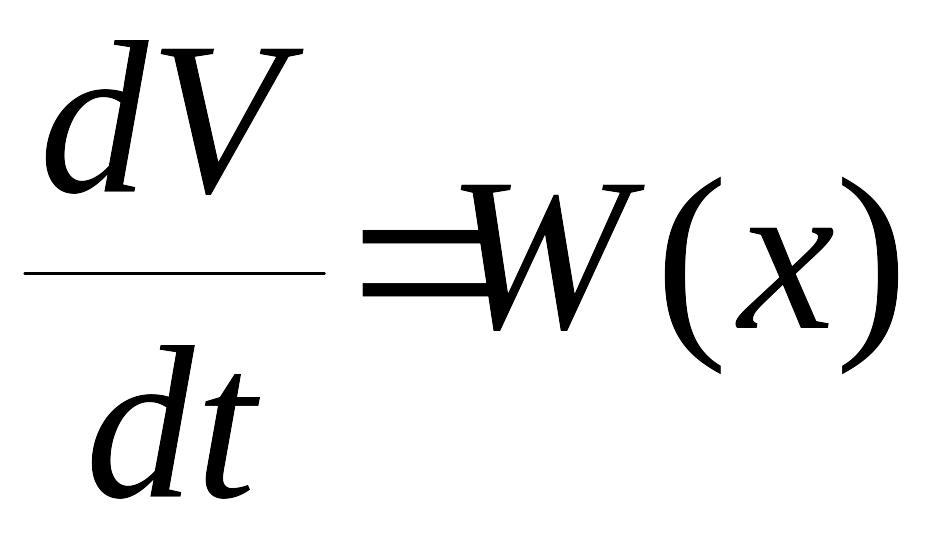является знакопостоянной противоположного знака, то решение системы устойчиво.

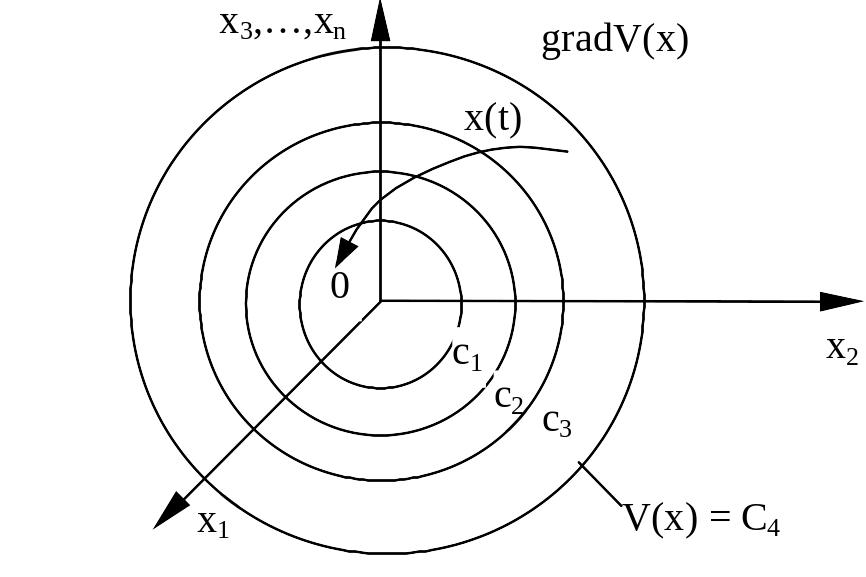
Рис. 5.

На рис. 5 представлена геометрическая иллюстрация этой теоремы, базирующаяся на свойстве (9) при условии и . При фазовая траектория пересекает поверхности V=C извне внутрь, а в случае она может остаться на такой поверхности. Поэтому в теореме говорится просто об устойчивости, но не об асимптотической.

Приведем доказательство теоремы. Зададим некоторое значение и область значений , ограниченную величиной . Пусть имеется определенноположительная функция . Обозначим точную нижнюю грань значений функции при через , т.е.

. (10)

Поскольку , то из непрерывности определенноподожительной функции следует, что можно взять такое значение , когда при будет 

Пусть начальные условия лежат внутри области , т.е. , и следовательно,  Тогда для решения при функция будет невозрастающей, так как по условию теоремы

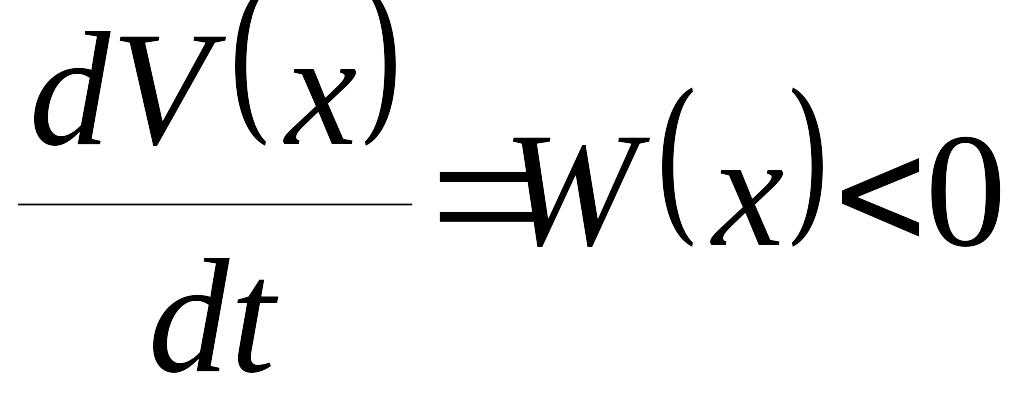. (11)

Итак, получаем

. (12)

При этом неизбежно будет

(13)

так как, если бы было , то получилось бы

,

что противоречит (12). Теорема доказана.

Из формулировки и из доказательства видно, что теорема Ляпунова дает достаточные условия устойчивости решения нелинейной системы. Значит, если условия теоремы удовлетворяются, то система устойчива. Но это не означает, что система не может быть устойчивой и за пределами этих условий. Насколько полно условия теоремы отражают действительную область устойчивости системы зависит от выбора функции Ляпунова .

Теорема Ляпунова об асимптотической устойчивости. Если для системы уравнений (6) существует знакоопределенная функция , производная которой является тоже знакоопределенной, но противоположного знака, то решение системы будет устойчивым ассимптотически.

Геометрическая иллюстрация теоремы может быть представлена тем же рис. 5, но только с той разницей, что при имеем здесь , и по свойству (9) фазовая траектория, пересекая поверхности извне внутрь, не может остаться на них, а пойдет внутрь вплоть до начала координат, где и .

Ход аналитического доказательства тоже остается прежним, но с изменением (11) на

.

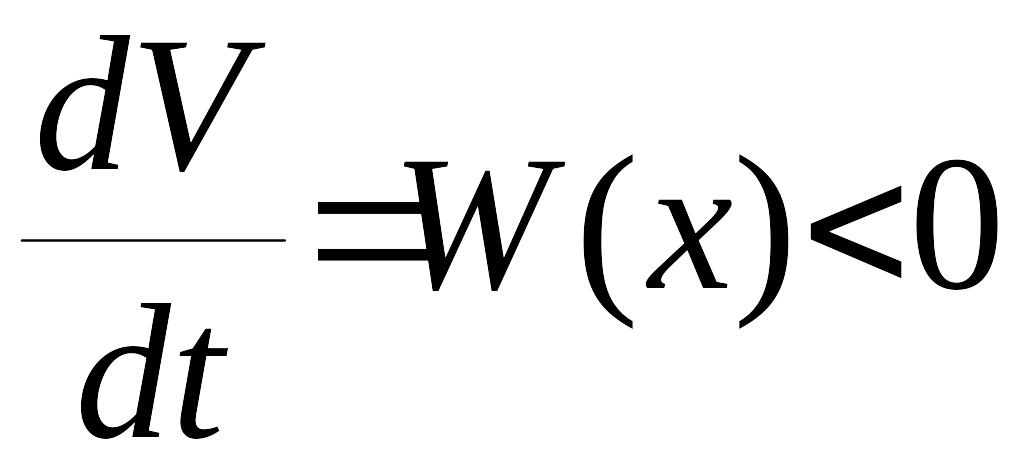В следствии чего, будет монотонно убывающей функцией с нижним пределом .Поэтому вместо (13) получаем .

Эта теорема, как и первая, тоже дает достаточные условия устойчивости, а полнота охвата действительной области устойчивости системы зависит от выбора функции Ляпунова .

Теорема Ляпунова о неустойчивости. Поскольку обе предыдущие теоремы Ляпунова дают достаточные условия устойчивости, вообще говоря, не охватывающие всю область устойчивости системы, то может представлять интерес определение условий, где система становится наверняка неустойчивой.

Теорема формулируется следующим образом. Если для системы уравнений (6) существует какая-нибудь функция , производная которой является знакоопределенной функцией, причем в любой сколь угодно малой окрестности начала координат, имеется область, в которой знак совпадает со знаком , то решение системы неустойчиво.

Приведем геометрическую иллюстрацию теоремы для случая на фазовой плоскости. Пусть функция знакопеременная с линиями , показанными на рис. 6., а ее производная определенноположительная. Видно, что при произвольных начальных условиях фазовая траектория, направляясь в соответствии со свойством (9), попадает в область, где , и будет удаляться от начала координат. Если же является определенноотрицательной, то фазовая траектория удаляется от начала координат в области, где .

Аналитически это описывается следующим образом. Пусть производная знакоопределенная положительная. Зададим некоторое значение . По условиям теоремы, как бы мала ни была область начальных условий , всегда найдется часть этой области, где будет функция . Тогда с течением времени будет возрастать, т.е. .

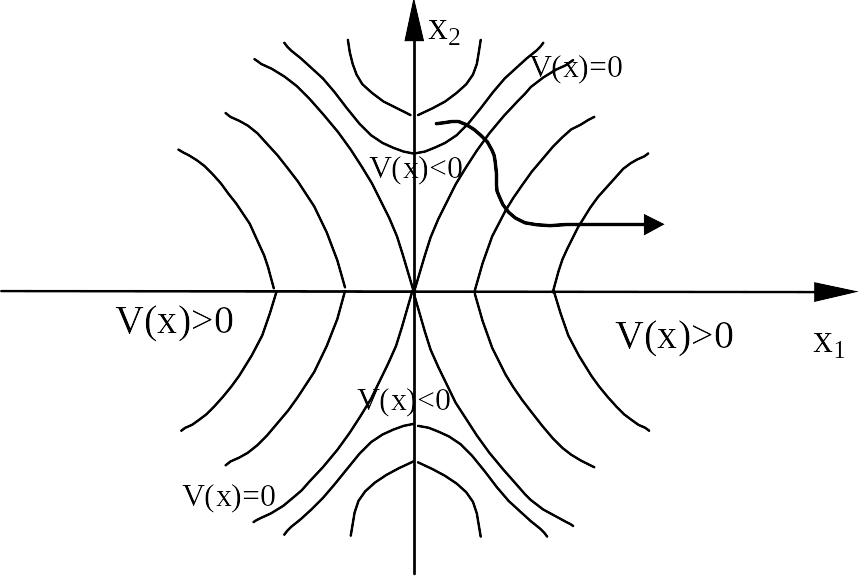
Рис. 6

Поэтому некоторый момент времени значение функции перейдет величину и затем станет больше ее, а вместе с этим будет и при и при любом заданном , что и говорит о неустойчивости системы.

Перейдем теперь к изложению методики применения теорем Ляпунова для исследования устойчивости нелинейных систем автоматического управления. Сделаем это для одного (достаточно широкого) класса систем с однозначной нелинейностью. Пусть система описывается следующими уравнениями в матричной форме

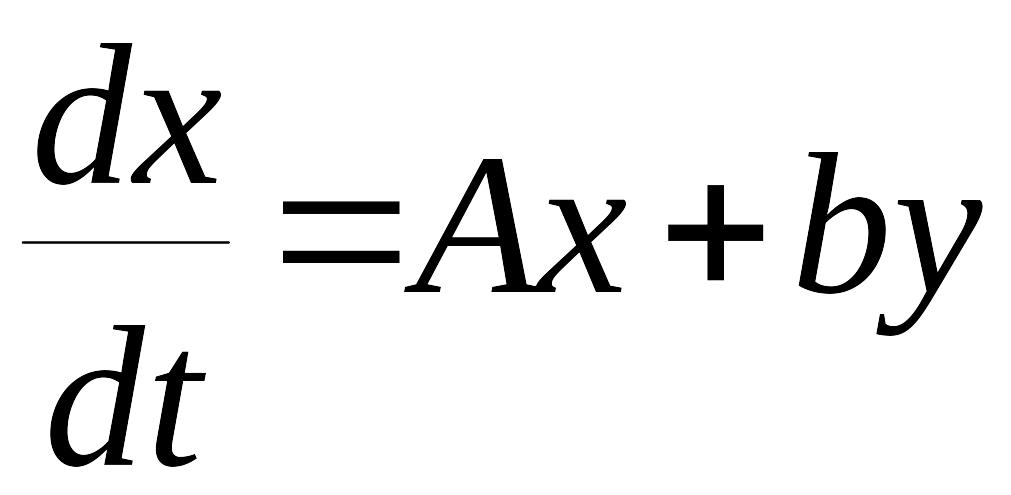, (14)

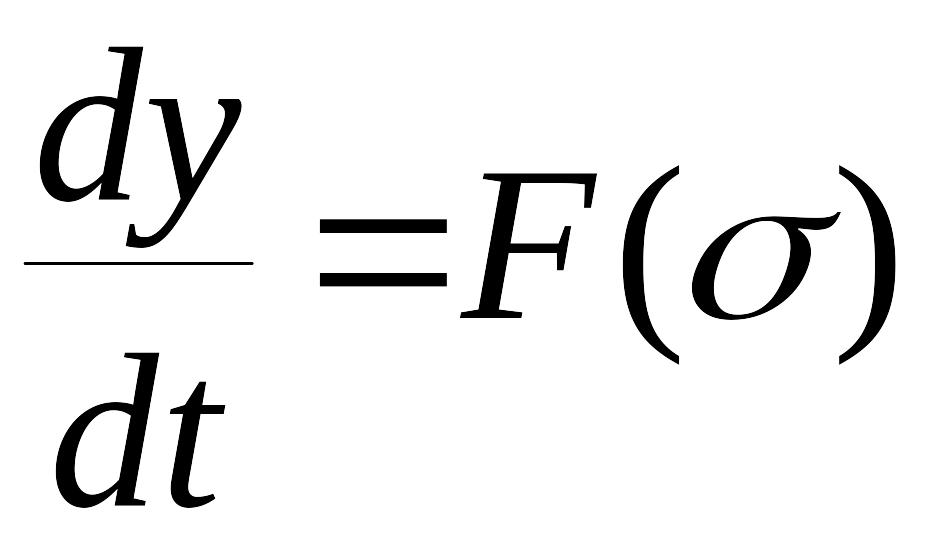, (15)

,

где – невырожденная матрица размера коэффициентов, ; - вектор, координатами которого являются переменные состояния системы ; и - скалярные функции; и - -мерные векторы коэффициентов, - скаляр, коэффициент обратной связи, - символ транспонирования.

Нелинейная функция может иметь произвольное нечетно‑симметричное очертание (рис. 7), удовлетворяющее условиям

. (16)

Общий порядок системы . В реальных системах измеряются не все координаты состояния объекта .Поэтому часть коэффициентов во втором уравнении (15) будут равны нулю.

Приведем заданную систему (14) – (15) к каноническому виду путем замены переменных

, .

Проделав это, получим систему уравнений

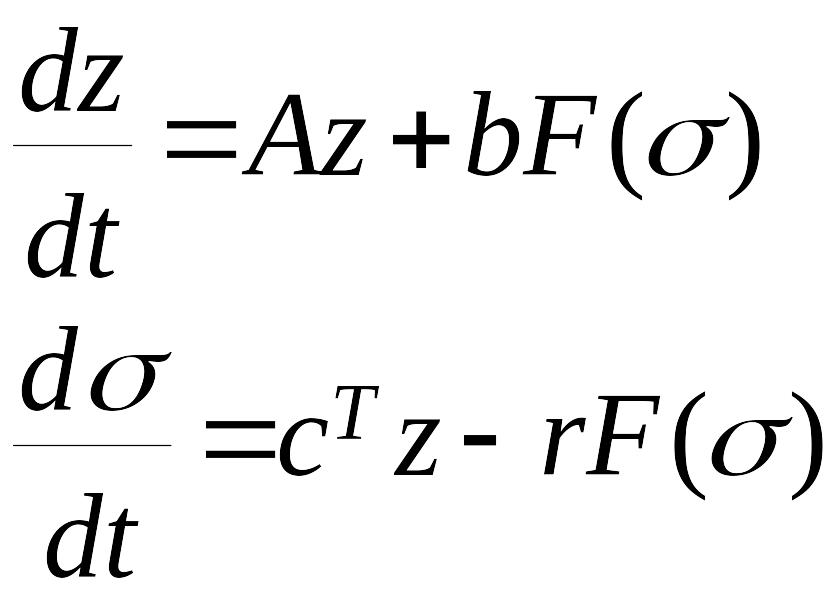, (17)

причем будем полагать, что матрица приведена к диагональной форме. Должно соблюдаться условие невырожденной общей матрицы системы

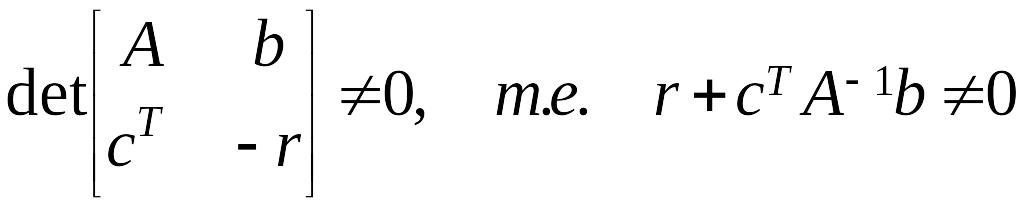. (18)

Функцию Ляпунова в этом случае рекомендуется брать в виде

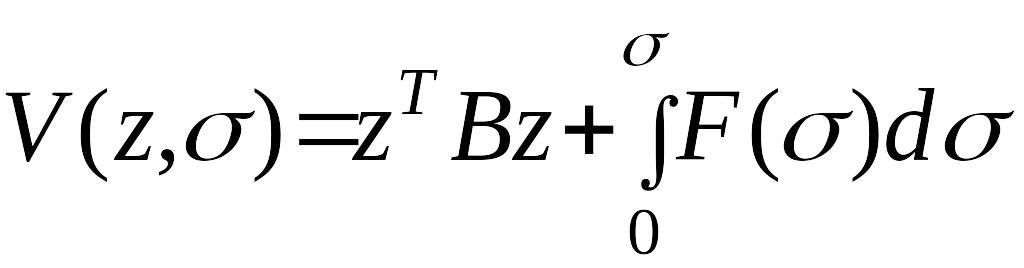, (19)

где – некоторая положительно определенная квадратичная форма n координат . Интеграл в этом выражении тоже является, как легко проверить, положительно определенной функцией – ой координаты .

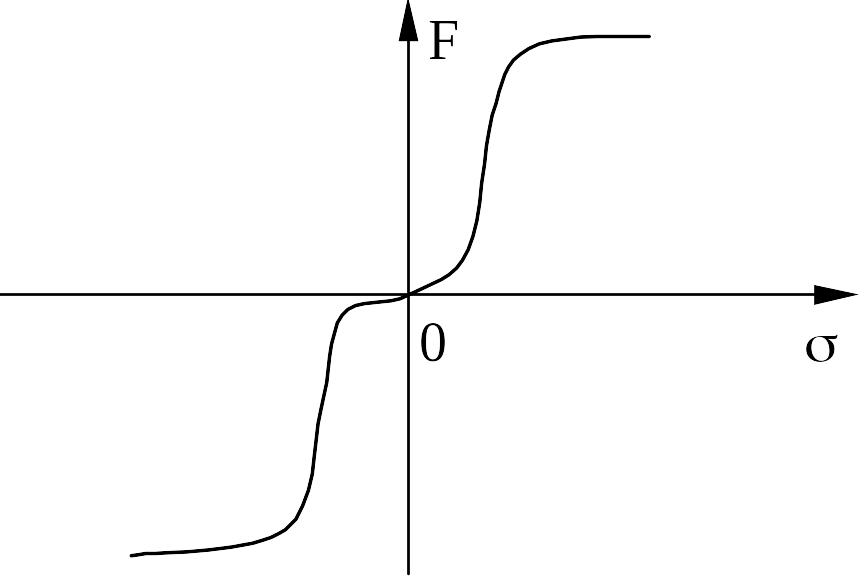
Рис. 7.

Рис. 8.

Составим производную функции Ляпунова (19) в силу уравнений системы (17). Имеем

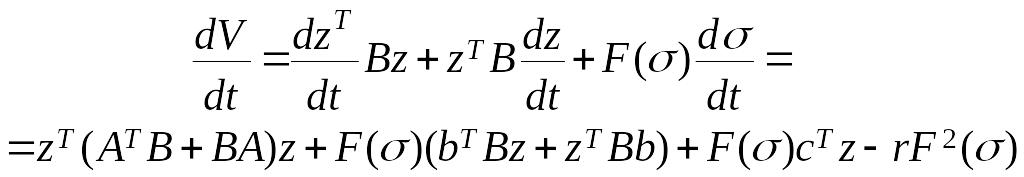
Матрица квадратичной формы B является симметричной, т.е. . Поэтому можно сделать следующее преобразование

.

Далее обозначим . И покажем, что матрица симметрическая. В самом деле

.

Итак, получаем

.

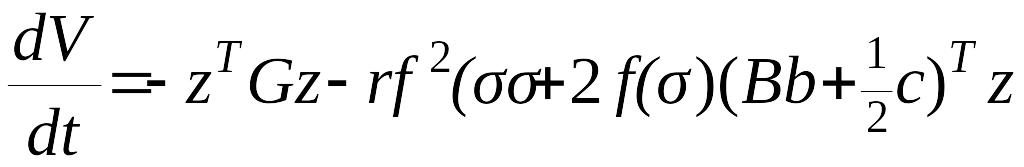Это выражение представляет собой квадратичную форму. Согласно теоремам Ляпунова об устойчивости, производная 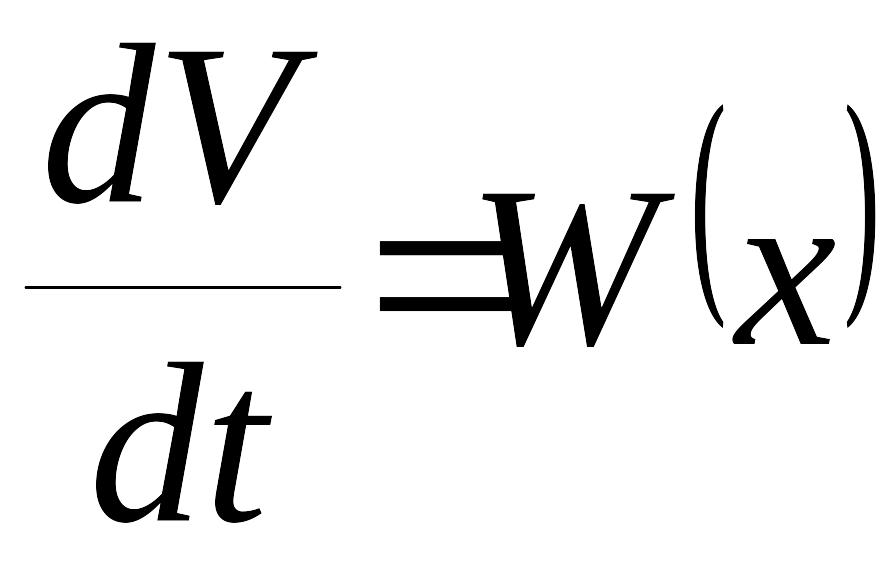должна быть закоопределенной, либо знакопостоянной отрицательной функцией. Обратимся к критерию Сильвестра для установления положительной определенности функции 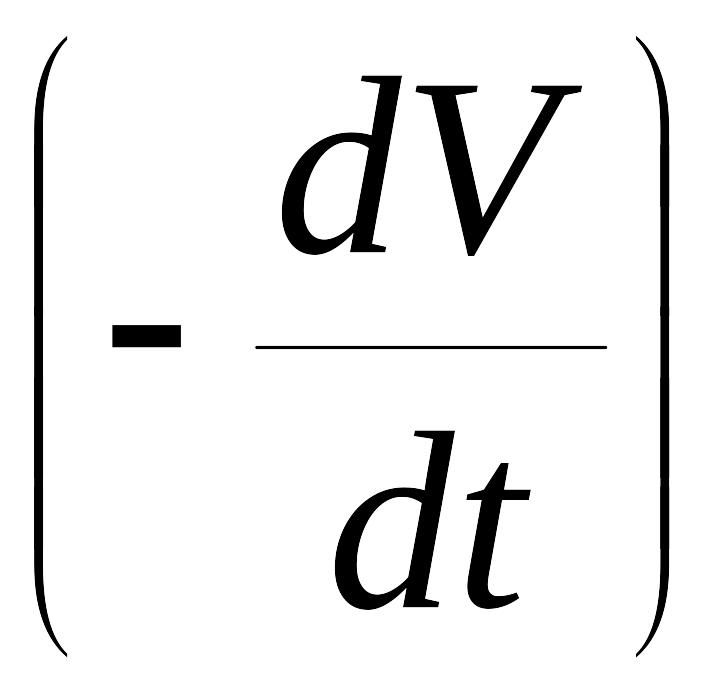. Поскольку является матрицей положительноопределенной квадратичной формы, то первые неравенств критерия Сильвестра выполняются. Остается потребовать

.

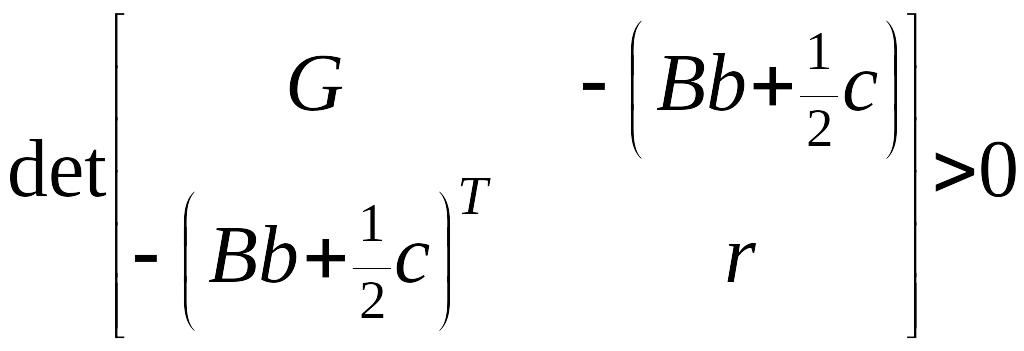Отсюда

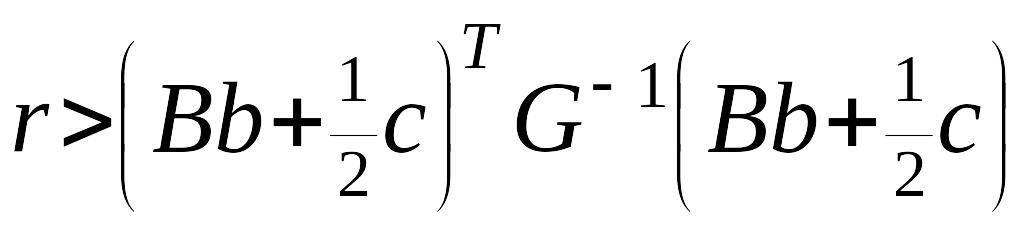. (20)

Следовательно, при выполнении этого условия (20) совместно с условием (18) система будет устойчива асимптотически. Это является достаточным условием асимптотической устойчивости решения , .

Видно, что в условия устойчивости (20) и (18) не вошли никакие параметры нелинейной характеристики . Следовательно, эти условия справедливы при любой форме нелинейности, удовлетворяющей общим требованиям (16). Такие условия устойчивости, которые не зависят от конкретной формы нелинейности, называются условиями абсолютной устойчивости системы.