Лекция 13. Исследование устойчивости нелинейных систем. Определение устойчивости, функции ляпунова.

Общее определение понятия устойчивости любой динамической системы по Ляпунову выглядит следующим образом. Запишем уравнения динамики нелинейной системы - ого порядка в нормальной форме Коши

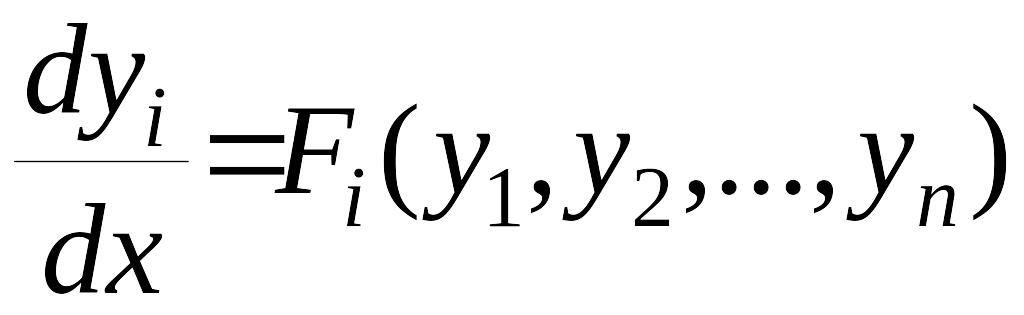, (1)

при отсутствии возмущающих воздействий. Устойчивость рассматривается как свойство свободного движения системы после начального отклонения ее, вызванного любыми причинами.

Пусть обозначает некоторый установившийся процесс работы системы или, как говорят, невозмущенное движение. Отклонение возмущенного движения , определяемого уравнениями (1) при определенных начальных условиях , обозначим через , т.е.

, . (2)

Тогда можно написать уравнения возмущенного движения в отклонениях в виде

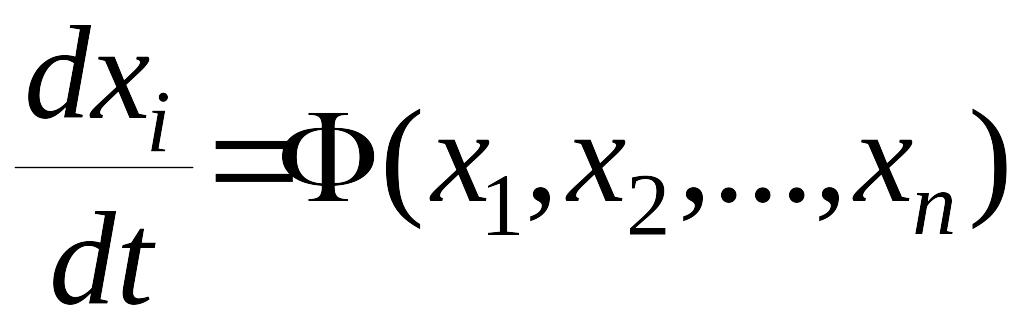, , (3)

а невозмущенное движение будет . Переменные являются координатами состояния системы.

В общем случае конкретное выражение уравнений (3) зависит от вида установившегося процесса , так как они получаются из (1) подстановкой (2). Поэтому, исследуя уравнения, вообще говоря, необходимо указывать – об устойчивости какого установившегося режима или невозмущенного движения идет речь.

Геометрически, невозмущенное (установившееся) движение системы - ого порядка можно представить условно в -мерном пространстве с добавлением еще оси времени (рис. 1) в виде некоторой интегральной кривой. Возмущенное движение , вызванное начальным отклонением при , изобразится другой интегральной кривой (рис. 1).

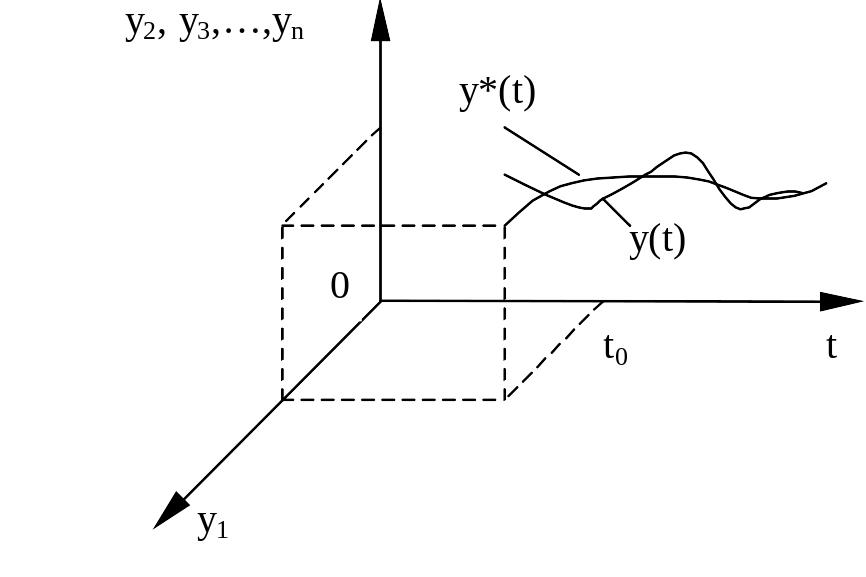
Рис. 1.

В отклонениях , т.е. в пространстве координат состояния системы, эта картина возмущенного движения будет выглядеть, как показано на рисунке 2. При этом невозмущенное движение изобразится прямой линией, совпадающей с осью .

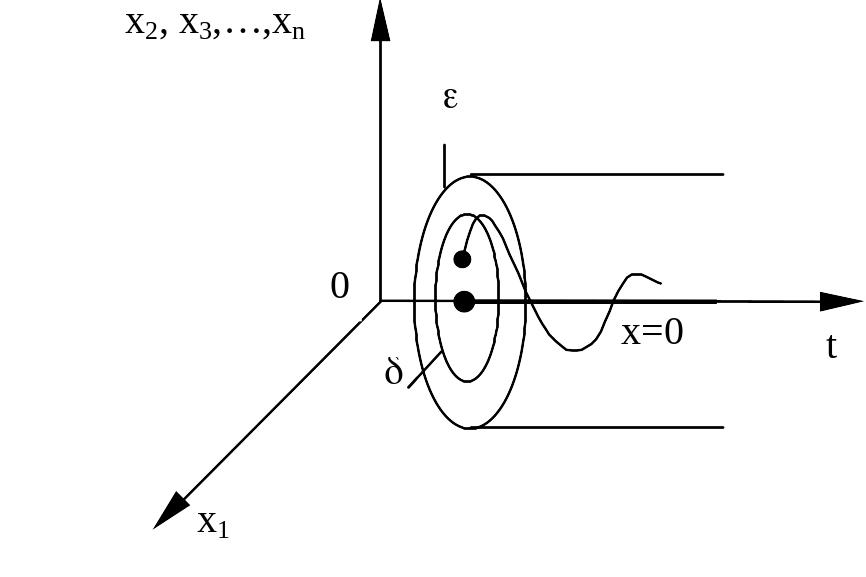
Рис. 2.

Невозмущенное движение системы называется устойчивым, если, задав «трубку» сколь угодно малого -мерного сечения (рис. 2), можно подобрать в начальный момент такую область начальных условий , зависящую от , что в дальнейшем с увеличением возмущенное движение не выйдет из заданной трубки .

Аналитическое определение понятия устойчивости по Ляпунову формулируется следующим образом.

Невозмущенное движение системы называется устойчивым, если при заданном , сколь бы оно мало ни было, существует такое , зависящее от , что при начальных условиях

, , (4)

в дальнейшем движении будет все время

, . (6.5)

Заметим, что в этом аналитическом определении области и , в отличие от рис. 2 выглядят "прямоугольными" (в n-мерном пространстве), что не имеет принципиального значе­ния.

Невозмущенное движение будет неустойчивым, если указанное условие не выполняется хотя бы для одного из .

Если при выполнении указанного выше определения имеем , то невозмущенное движение называется асимптотически устойчивым.

Если же после любых больших начальных отклонений, то система называется устойчивой в целом.

Существует еще понятие абсолютной устойчивости, означающее устойчивость системы в целом при любом очертании нелинейности внутри определенного класса нелинейностей.

В общем случае в нелинейных системах, в отличие от линейных устойчивость состояния равновесия не означает, что будут устойчивы и все процессы в системе, так как свойства нелинейной системы меняются с изменением размера отклонений координат состояния. Наглядным примером может служить наличие в системе второго порядка неустойчивого предельного цикла . В этом случае при устойчивом состоянии равновесия система оказывается неустойчивой при больших начальных отклонениях (выходящих за границу предельного цикла), т.е. система устойчива "в малом" и неустойчива "в большом".

При определении понятия устойчивости рассматривались интегральные кривые (рис. 1 и 2), Если же представить себе не интегральную кривую, а фазовую траекторию в -мерном пространстве для системы уравнений (3), то в устойчивой системе согласно определению она будет иметь вид, изображенный на рис. 3.

Рис. 3.

Далее придется иметь дело с непрерывными функциями координат состояния системы обладающими свойством при .

Такая функция называется знакоопределенной функцией если во всей рассматриваемой области окружающей начало координат, она сохраняет один и тот же знак и обращается в нуль только в точке начала координат. Например, при .

Знакоопределенная функция может быть положительноопределенной или отрицательноопределенной

Если же функция сохраняет один и тот же знак, но обращается в нуль не только в начале координат, то такая функция называется знакопостоянной (положительной или отрицательной). Например, при обращается в нуль на прямой и .

Наконец, функция будет знакопеременной, если обращаясь в нуль в начале координат (и не только), она в рассматриваемой области не сохраняет одного и того же знака. Например, .

Согласно известному критерию Сильвестра, любая квадратичная форма координат будет знакоопределенной (положительной) тогда и только тогда, когда все главные диагональные миноры матрицы ее коэффициентов будут положительны. Например,

будет положительноопределенной, так как для матрицы ее коэффициентов

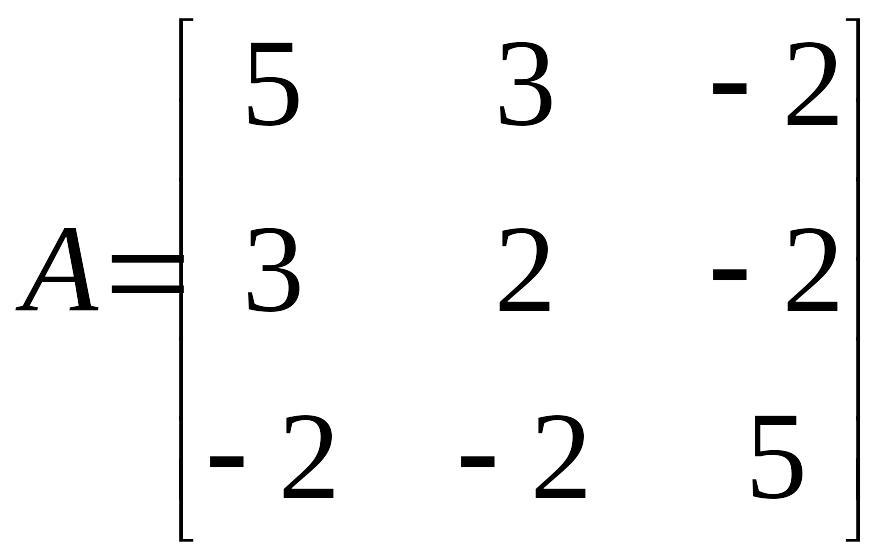
имеем

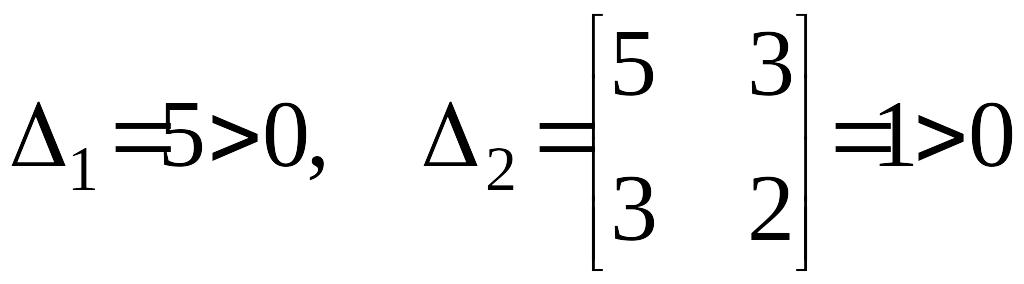
и, наконец,

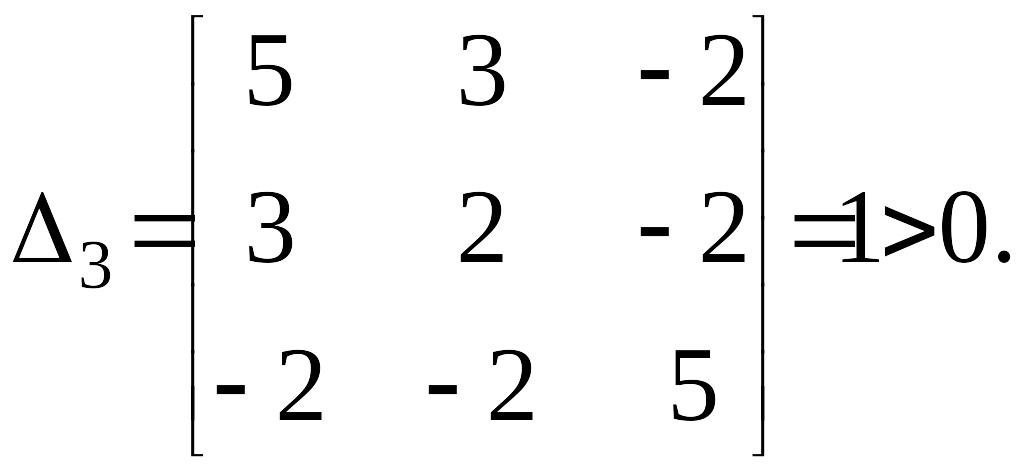
Описанные функции от координат состояния системы, обращающиеся в нуль в начале координат, играют важную роль в теоремах Ляпунова об устойчивости и неустойчивости нелинейных систем и называются функциями Ляпунова.

Пусть имеется нелинейная система, описываемая уравнениями динамики

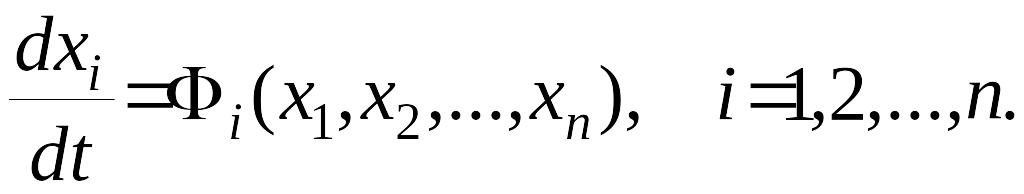(6)

Составим производную функции Ляпунова в силу уравнений системы

.

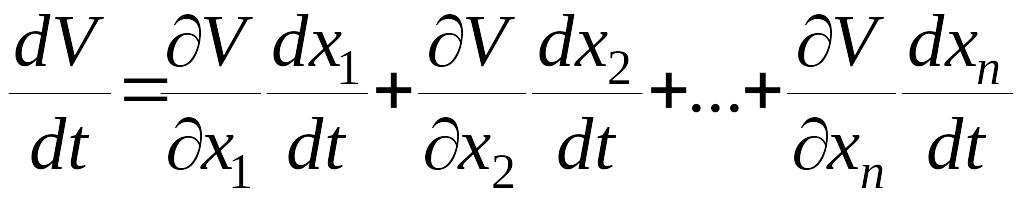Используя уравнение (6), найдем

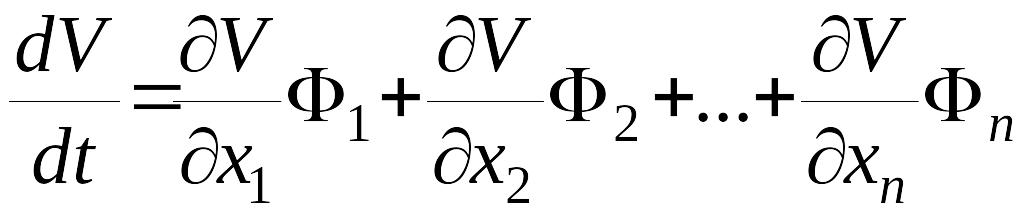. (7)

Очевидно, что в результате тут получается тоже некоторая функция координат состояния системы

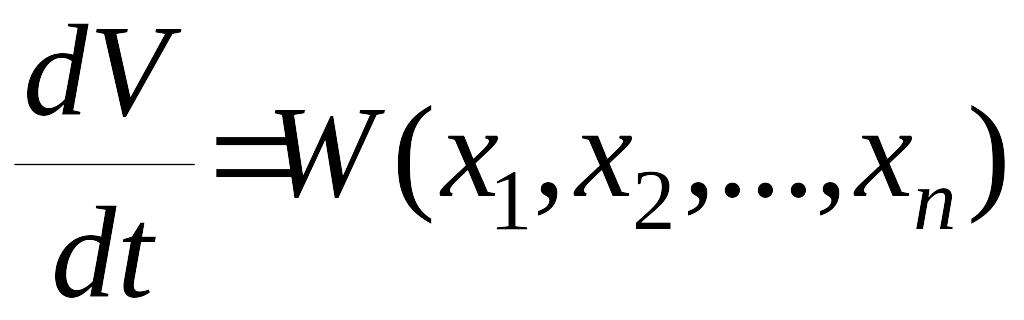. (8)

Известно далее, что градиент функции есть вектор, определяемый следующими проекциями

.

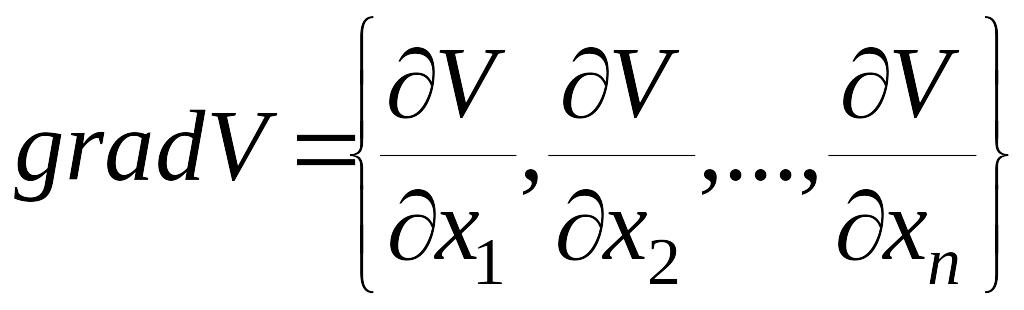Можно ввести вектор с проекциями, отвечающими уравнениям (6), а именно .

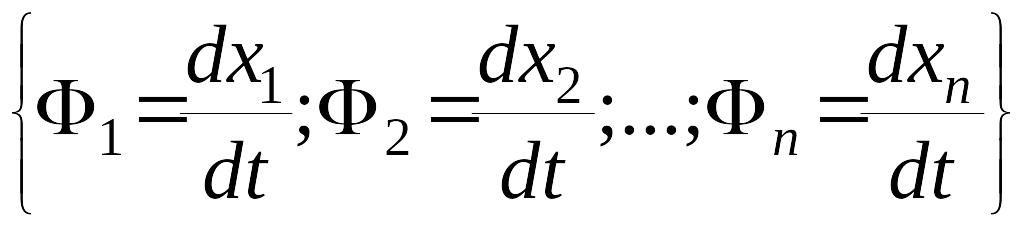Вектор будет вектором скорости изображающей точки в фазовом пространстве (рис. 4).

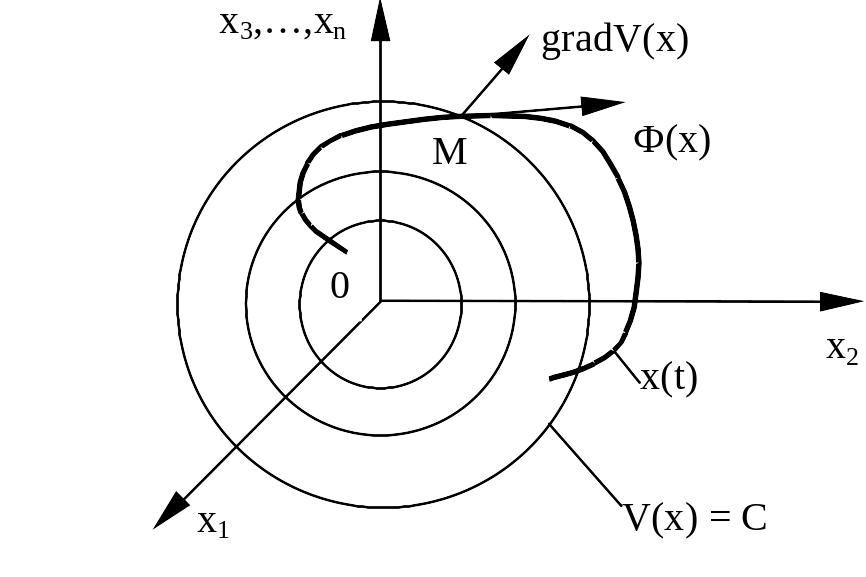
Рис. 4

Согласно (7) получаем

,

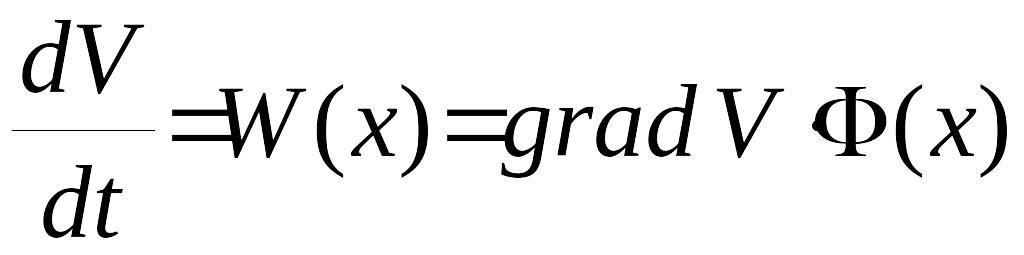где под подразумевается совокупность всех координат состояния системы .

Итак, производная функции Ляпунова, составленная в силу уравнений системы, представляет собой скалярное произведение градиента этой функций на вектор фазовой скорости.

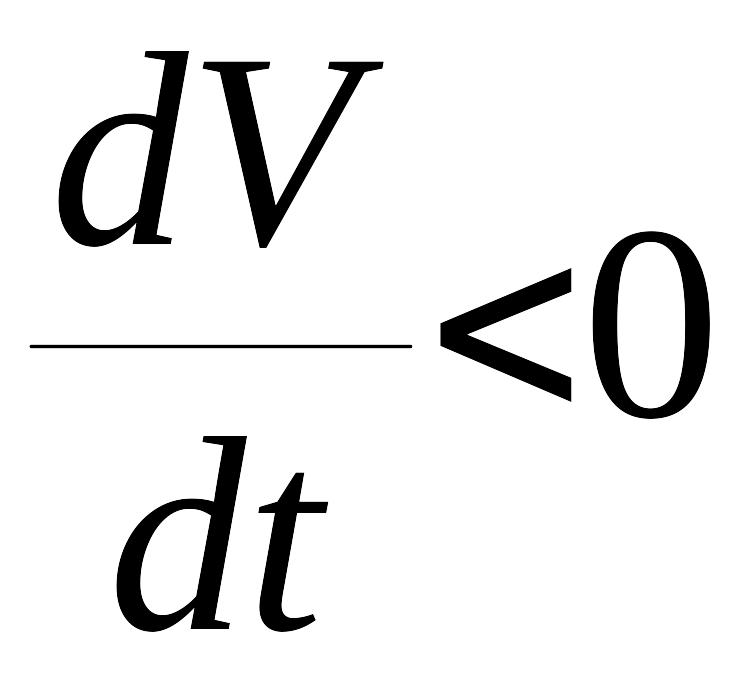Вектор перпендикулярен к поверхности и направлен в сторону возрастания значения (рис.4). Если производная положительна, то согласно (9) вектор фазовой скорости составляет с острый угол, т.е. фазовая траектория пересекает поверхность в сторону увеличения значений . Если же , угол между и тупой, и фазовая траектория идет в сторону уменьшения значений .