Лекция 10. Методы определения амплитуды и частоты автоколебаний в нелинейных системах автоматического управления

Постановка задачи. Рассмотрим замкнутую систему автоматического управления, структурную схему которой можно представить в следующем виде

где 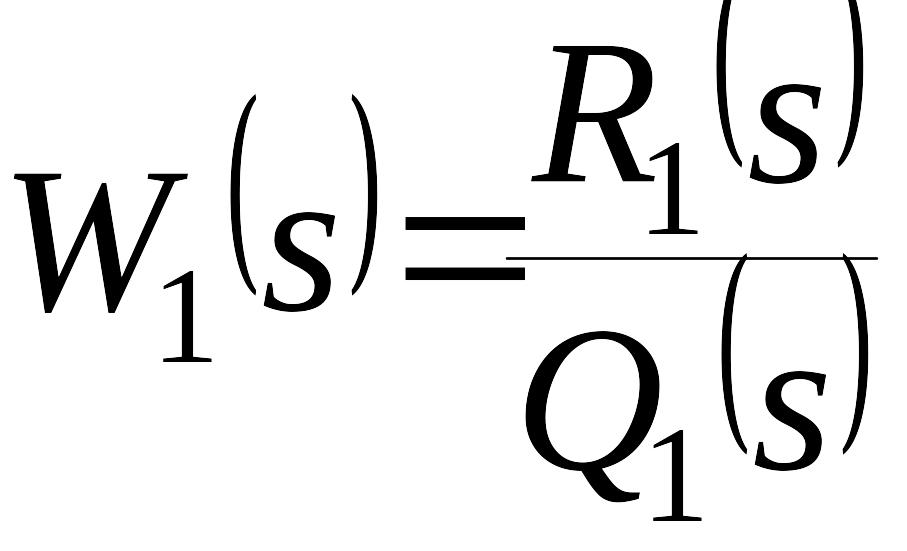, , 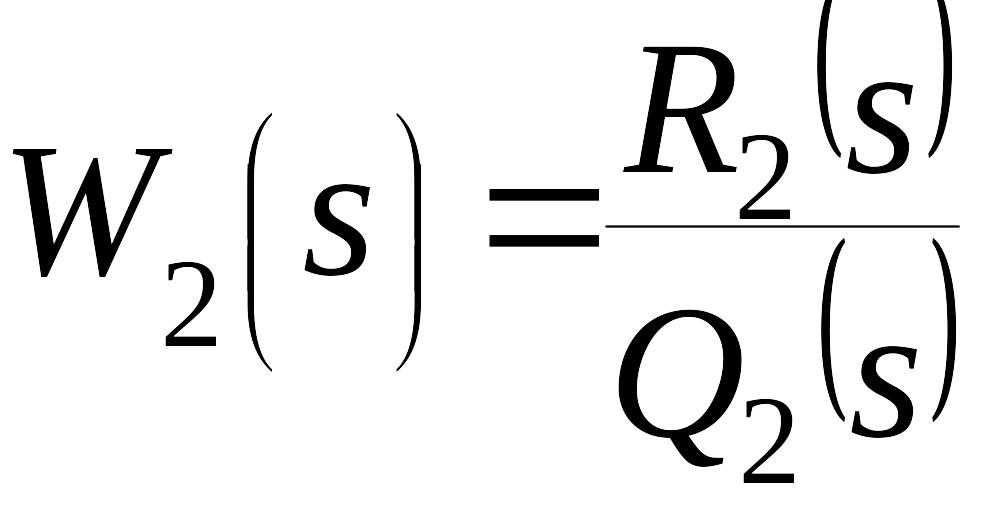– симметричная функция, характеристика нелинейного звена.

Получим уравнения, описывающие процессы в системах при

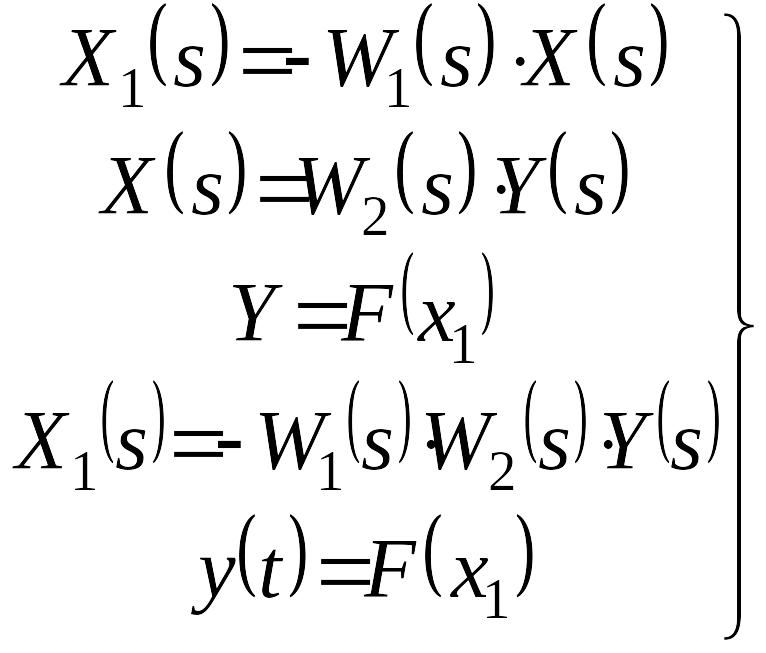, (1)

,

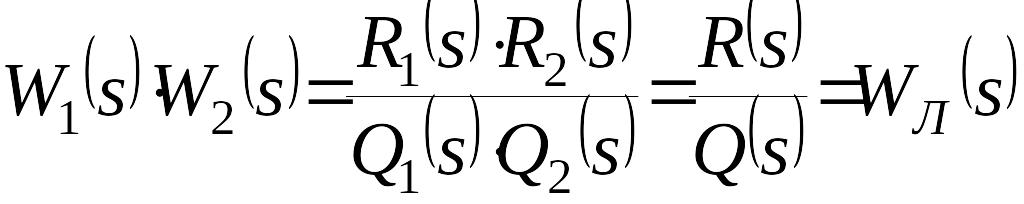где – передаточная функция линейной части системы.

Исходные положения.

1. В исследуемой нелинейной системе автоматического управления имеют место автоколебания, период которых равен 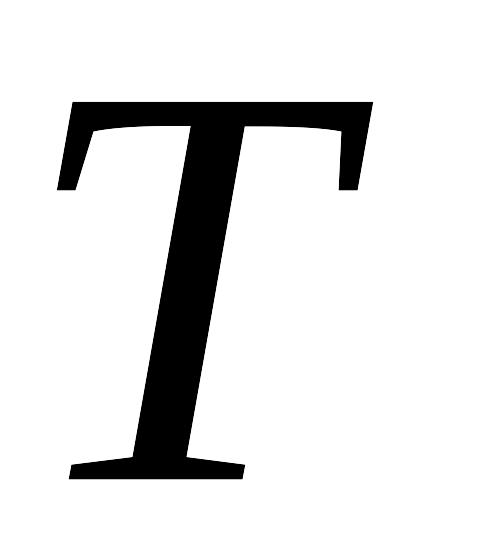(частота ).

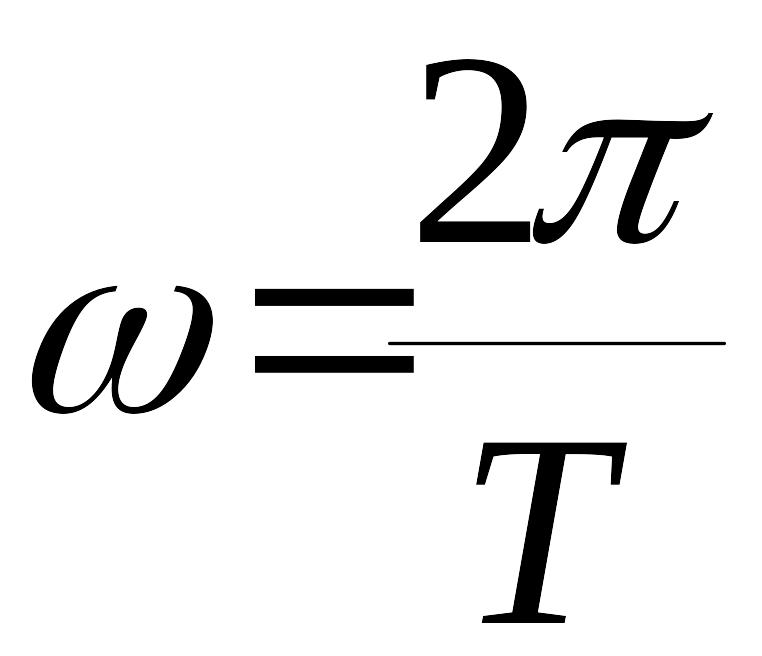2. Линейная часть системы управления обладает свойством фильтра, т.Е. , , следовательно, переменную можно представить в виде , .

3. Нелинейный элемент с характеристикой можно заменить гармонически линеаризованным звеном

,

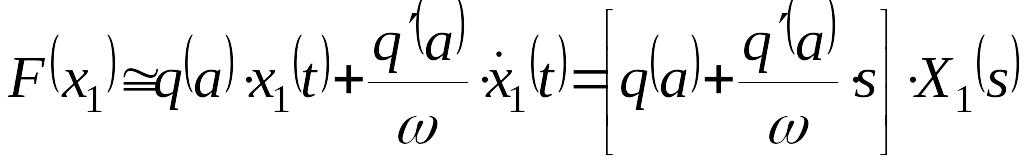где и – коэффициенты гармонической линеаризации, которые вычислены по формулам

, .

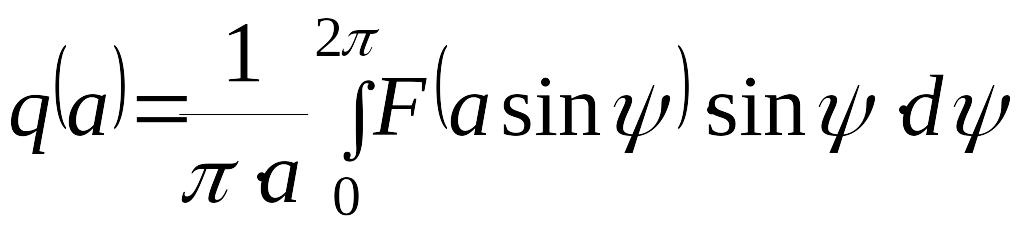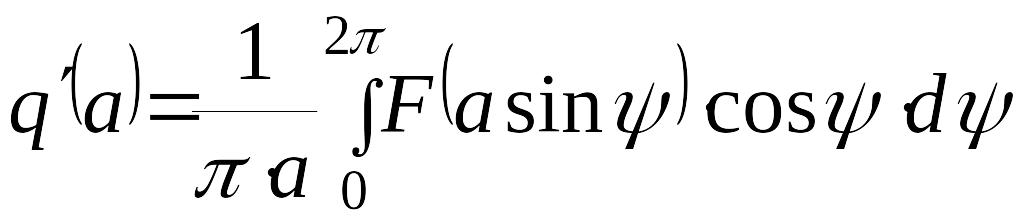4. Нелинейную систему автоматического управления представим приближенной гармонически линеаризованной системой, структурная схема которой имеет вид

где 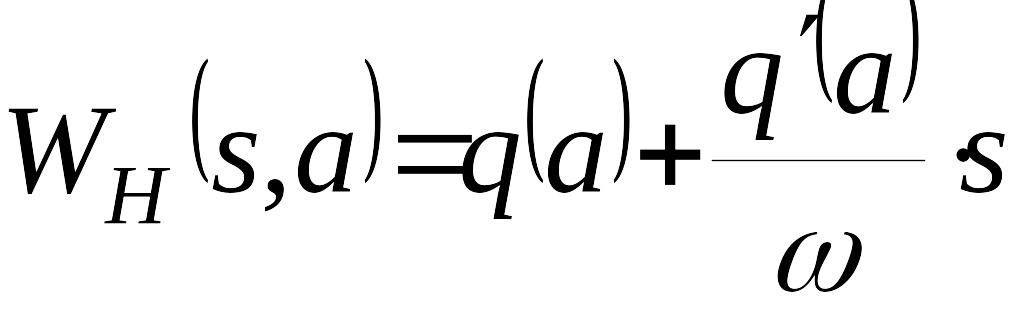– передаточная функция гармонически линеаризованного звена.

Существенно. Амплитуда и частота автоколебаний неизвестны, Все построения по замене нелинейной системы гармонически линеаризованной системой выполнены в предположении, что в системе возникли автоколебания периода .

Задача состоит в том, чтобы найти параметры автоколебаний – амплитуду и частоту , если автоколебания существуют.

Задача решается в три этапа.

1. Получение уравнений для определения параметров периодического решения.

2. Решение полученных уравнений аналитическим, численным или графо - аналитическим методом.

3. Анализ устойчивости периодического решения.

Если периодическое решение – устойчиво, то в системе есть автоколебания.

Методы решения задачи определения параметров автоколебаний можно разделить на

1. Алгебраические методы.

2. Частотные методы.

Все методы определения параметров автоколебаний преследуют одну и ту же цель, но в различных конкретных задачах может оказаться удобным тот или иной из них.

Алгебраические методы

1. Основан на непосредственном использовании характеристического уравнения гармонически линеаризованной системы.

2. Основан на использовании критерия Гурвица к гармонически линеаризованной системе.

Лекция 11. Алгебраический метод определения параметров периодических решений нелинейных систем.

Пусть структурная схема гармонически линеаризованной системы имеет вид

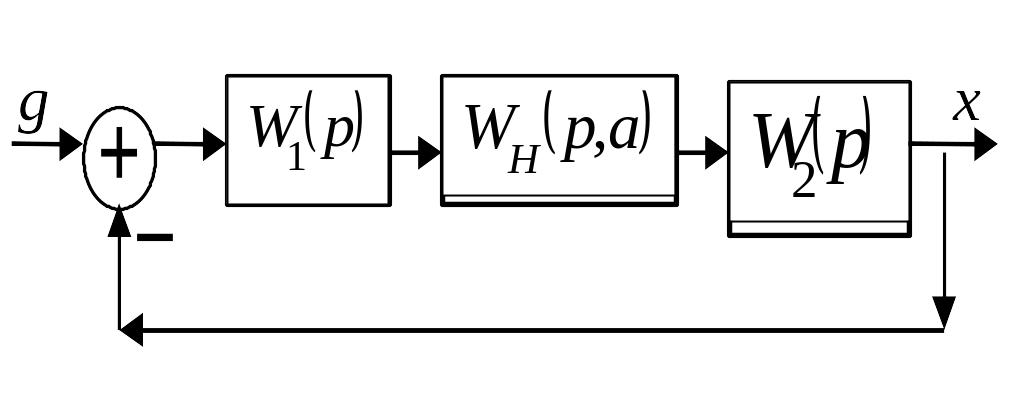
Составим уравнения гармонически линеаризованной системы уравнения при

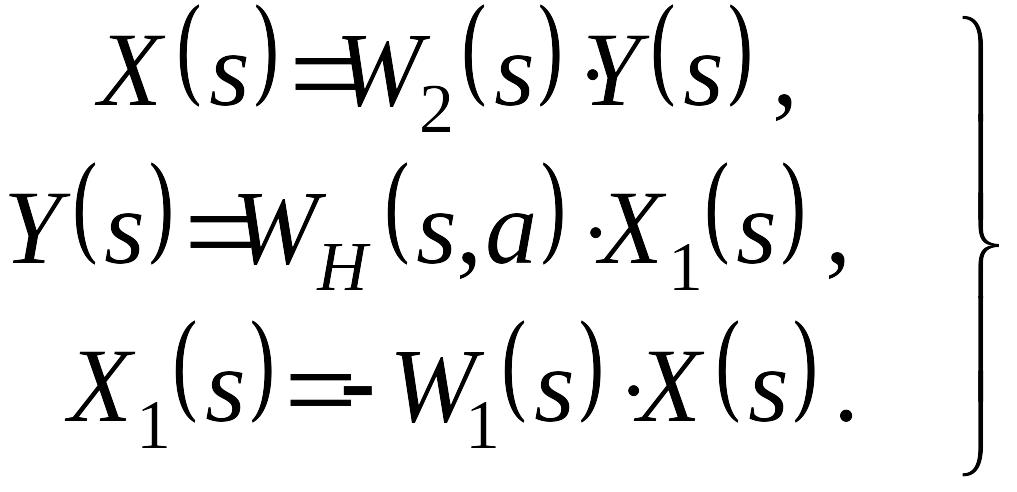(1)

Из уравнений (1) исключим и

,

. (2)

Из уравнений (2) окончательно получаем

.

С учетом того, что

, ,

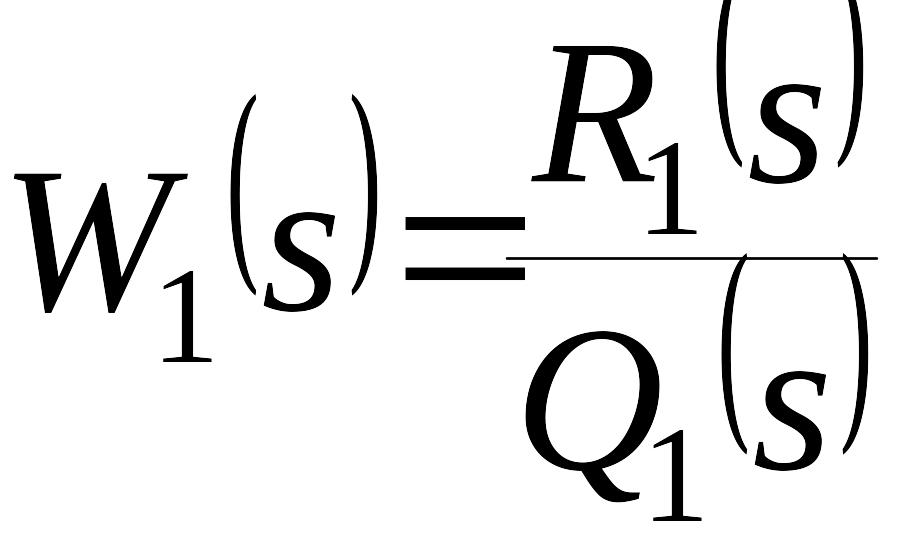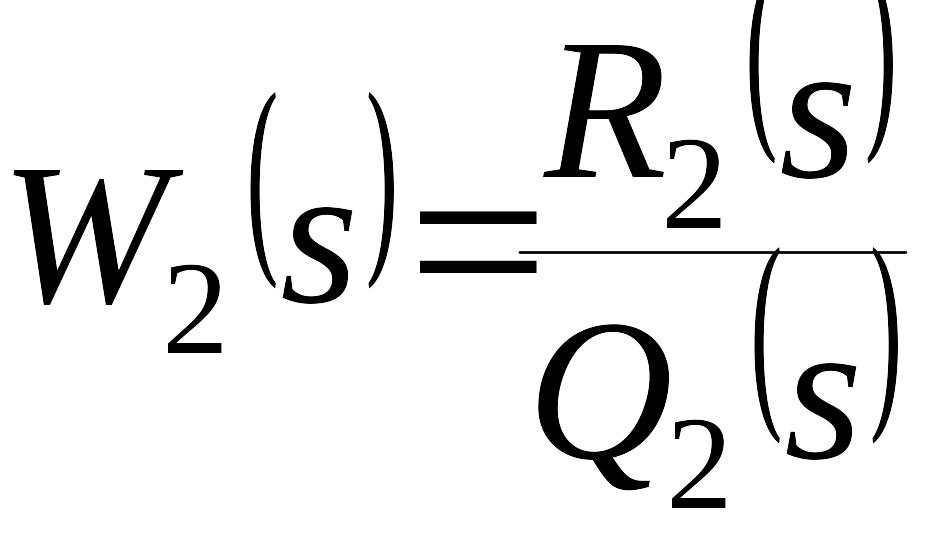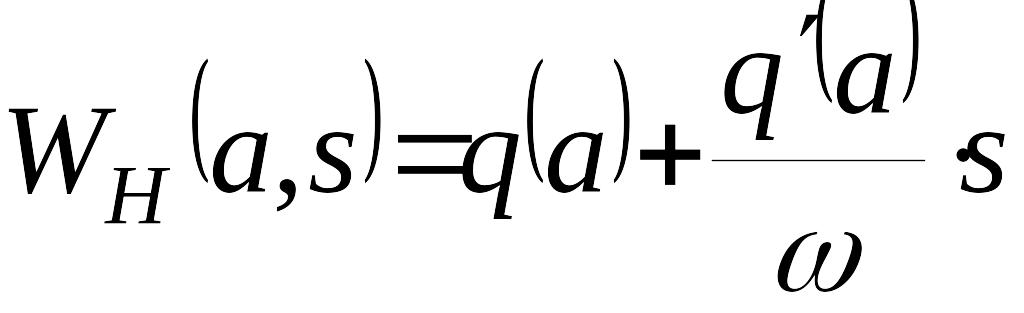
последнее уравнение можно переписать следующим образом:

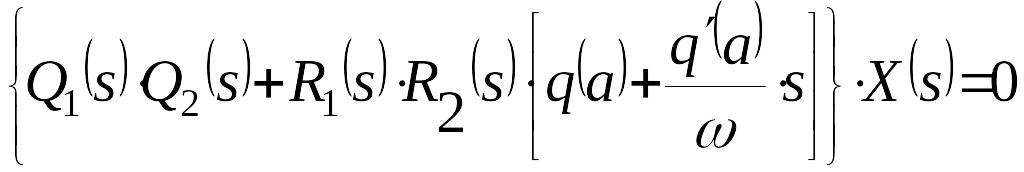
Таким образом, характеристическое уравнение исследуемой, гармонически линеаризованной системы имеет вид

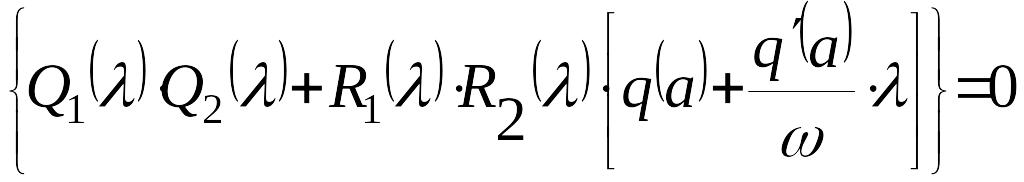
или, обозначив через

,

имеем

.

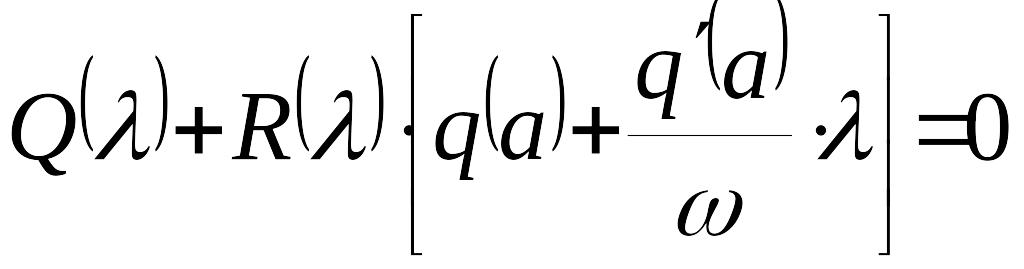Особенность уравнения (4). Уравнение (4) имеет неизвестные коэффициенты, т.к. амплитуда автоколебаний и их частота пока неизвестны. Если в системе существуют автоколебания (периодические режимы, решения, переменная ), то характеристическое уравнение (4) должно иметь пару чисто мнимых корней , а это значит, что комплексное число должно быть решением характеристического уравнения (4). Подставим в уравнение (4), получим

.

В последнем выражении выделим действительную и мнимую части

.

Это комплексное число, оно равно нулю в том и только в том случае, когда

, . (5)

Получили систему двух уравнений относительно искомых неизвестных параметров периодических процессов в системе – амплитуды и – частоты. Если система уравнений (5) имеет хотя бы одно решение, то в системе возможны периодические процессы. Но, как правило, система уравнений (5) может иметь несколько решений Полученное периодическое решение может представлять собой либо автоколебания, если оно устойчиво; либо границу для начальных условий между устойчивостью системы в малом или неустойчивостью в большом; либо иметь более сложный сигнал, если существует не одно периодическое решение.

Рассмотрим частный случай однозначной нечетной нелинейной функции . В случае однозначной нечетной функции коэффициенты гармонической линеаризации и . Следовательно, характеристическое уравнение гармонически линеаризованной системы имеет вид

, (6)

После подстановки в уравнение (6) получаем

. (7)

Выделим в полученном уравнении действительные и мнимые части в и получим

,

.

С учетом этих равенств уравнение (7) преобразуется следующим образом:

,

.

Из последнего уравнения получаем

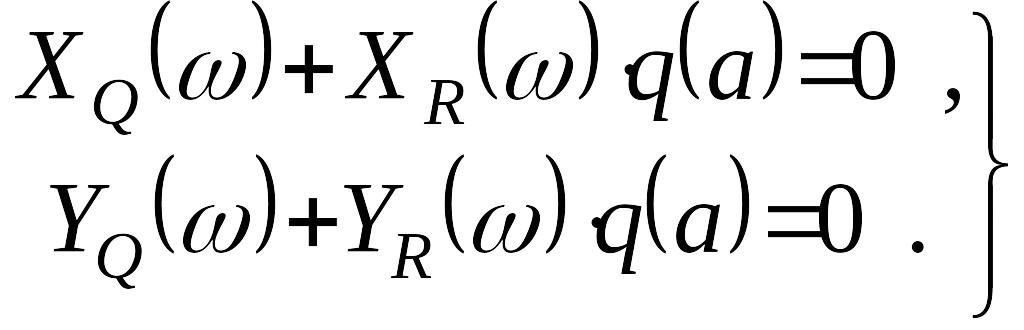(8)

систему двух уравнений относительно двух неизвестных и . Из уравнений (8) имеем

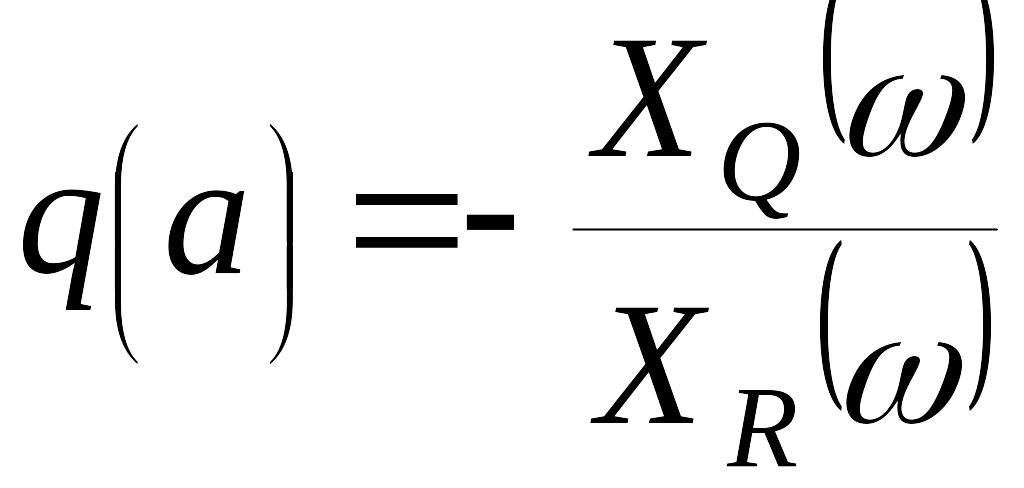, . (9)

Из второго уравнения системы (9) определяем частоты автоколебаний , а из первого уравнения системы (9) соответствующие им амплитуды автоколебаний .

Важно. Значения определяются только параметрами линейной части исследуемой системы автоматического управления и не зависят от вида однозначной нелинейной характеристики . Амплитуда автоколебаний определяется как параметрами линейной части системы так и параметрами и свойствами нелинейного звена системы.

После определения параметров периодического решения , необходимо исследовать каждое из них на устойчивость. Если периодическое решение устойчиво, то в системе существуют автоколебания.