4. Коэффициенты гармонической линеаризации.

Базируясь на свойстве фильтра линейной части системы в равенстве

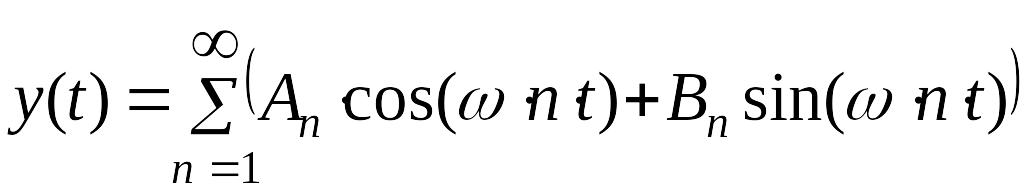
слагаемые можно не учитывать. Тогда

,

где

,

.

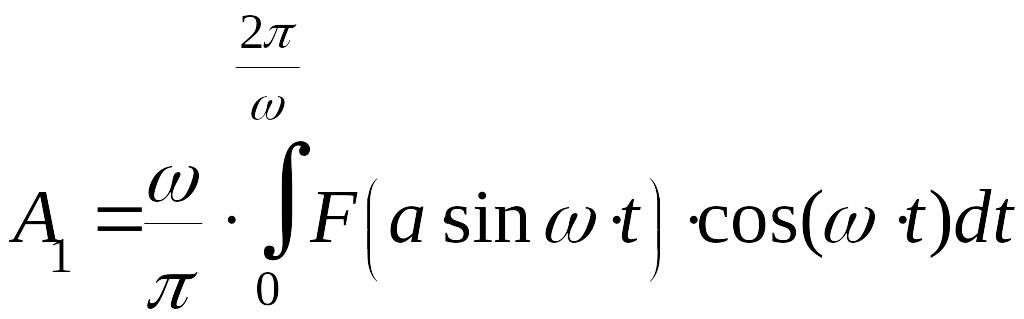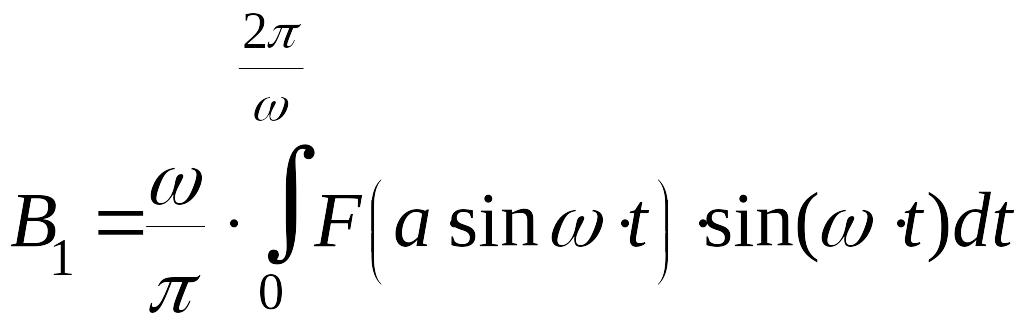Обозначим через 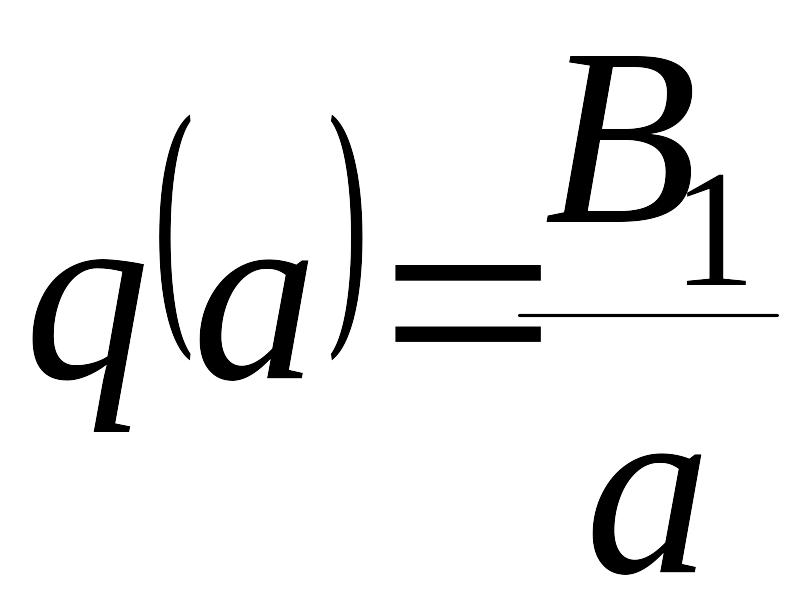и 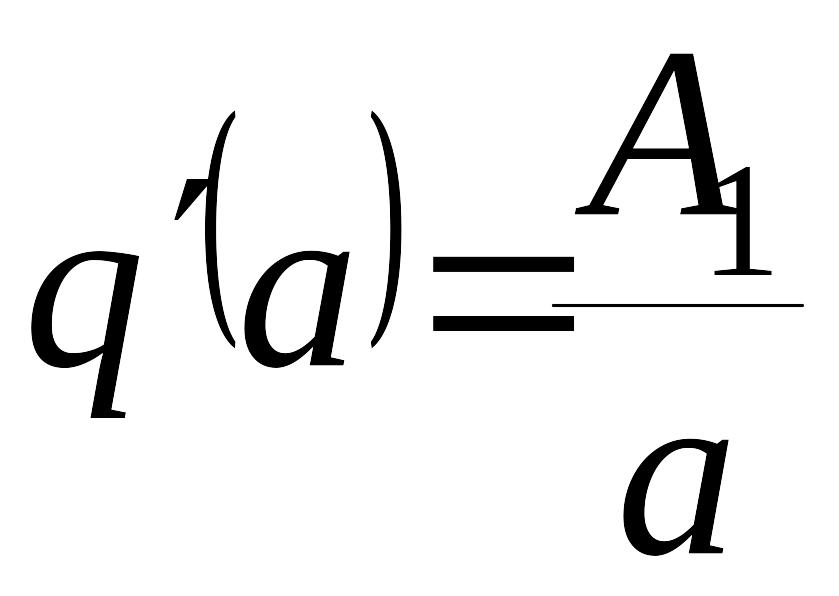. Пусть далее , тогда значения и вычисляются по формулам

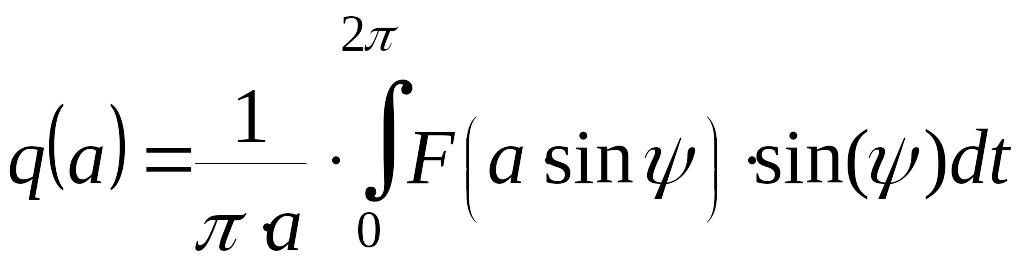, (1)

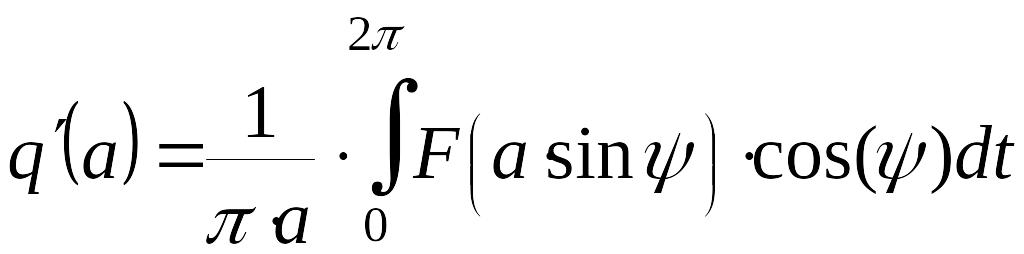. (2)

Величины и называются коэффициентами гармонической линеаризации.

VI. Гармонически линеаризованное нелинейное звено.

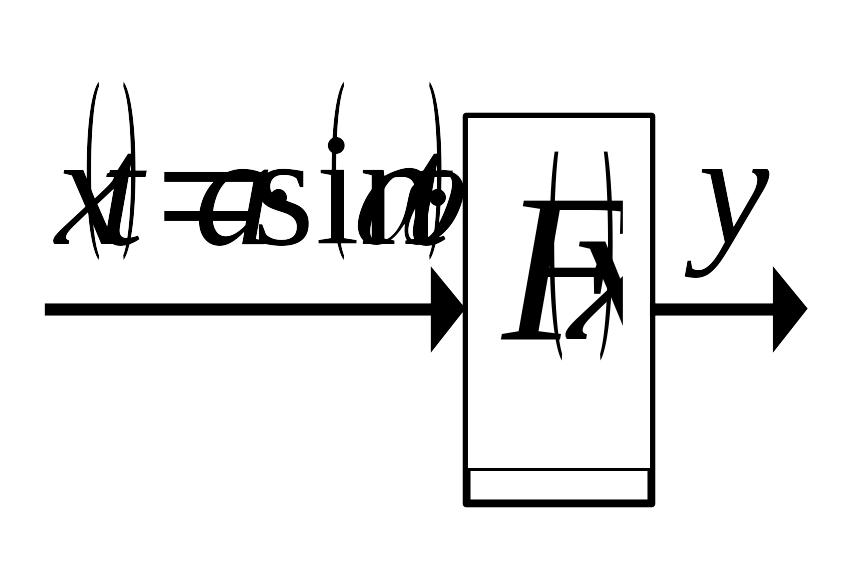
С учетом введенных коэффициентов гармонической линеаризации и равенство можно переписать следующим образом , но, заметив, что получаем

,

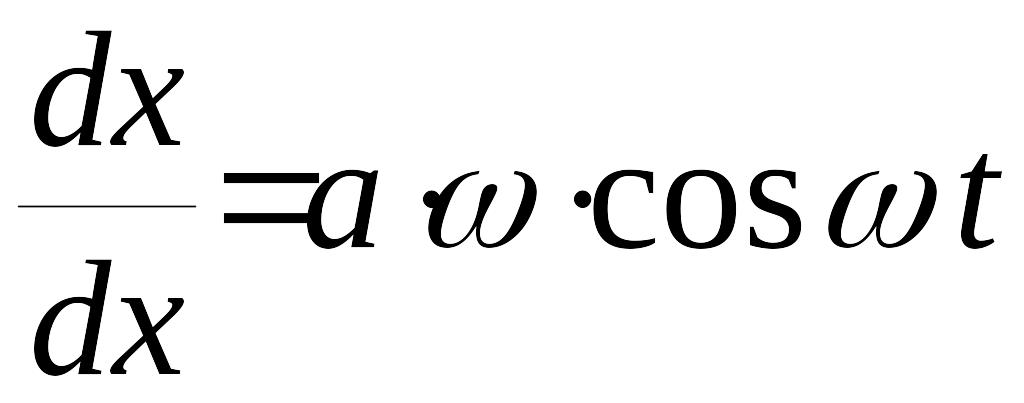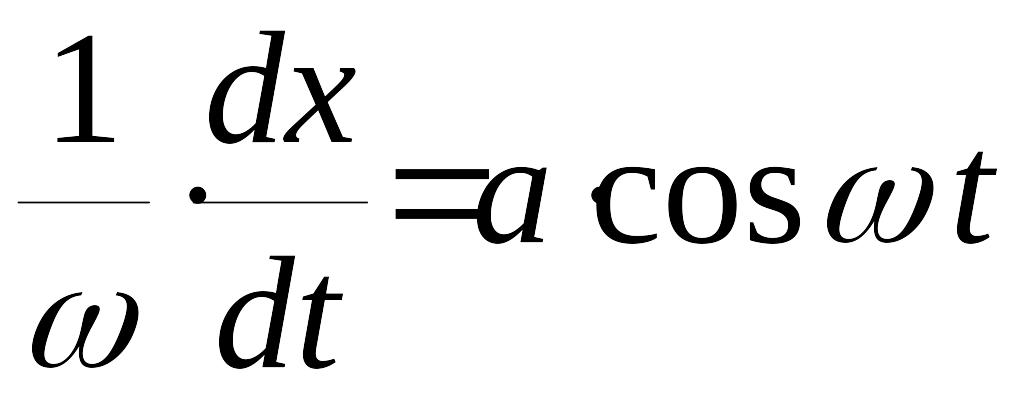
и, следовательно,

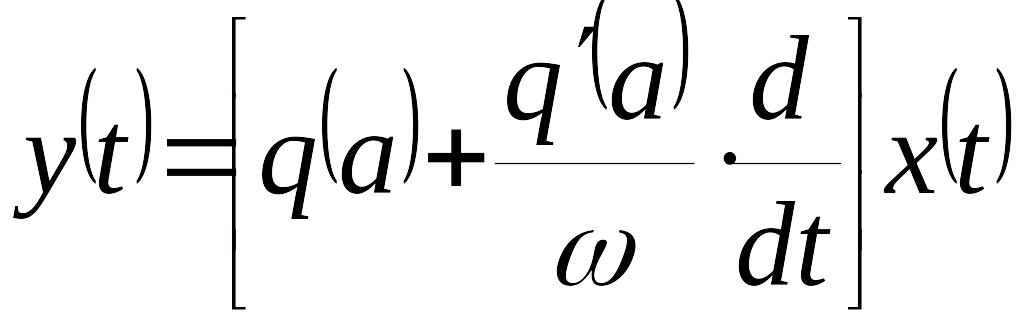. (3)

Представление (3) называется гармонической линеаризацией нелинейного звена. Равенство (3) является линейным относительно переменной при , т.е. только для данного конкретного периодического решения . Но в целом она сохраняет нелинейные свойства, т.к. его коэффициенты зависят от искомого решения, от величины амплитуды колебаний переменной . Эта особенность гармонической линеаризации и позволяет нам в дальнейшем исследовать с ее помощью основные свойства и особенности процессов в нелинейных системах.

При фиксированном значении и нулевых начальных условиях выполним преобразование по Лапласу равенства (3)

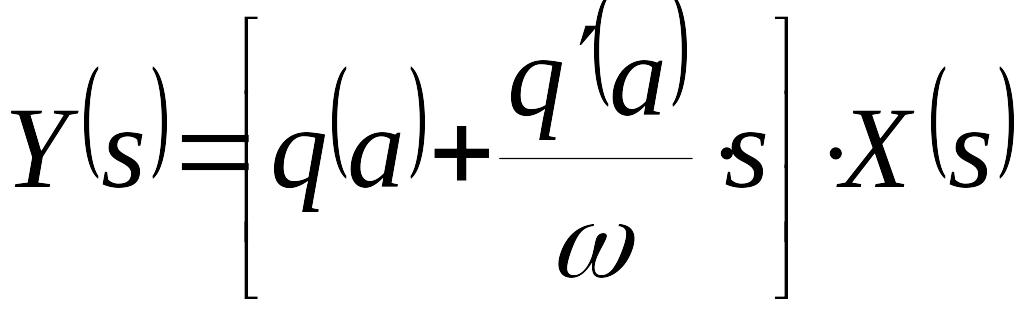. (4)

Таким образом, в результате гармонической линеаризации нелинейный элемент системы автоматического управления заменяется гармонически линеаризованным звеном

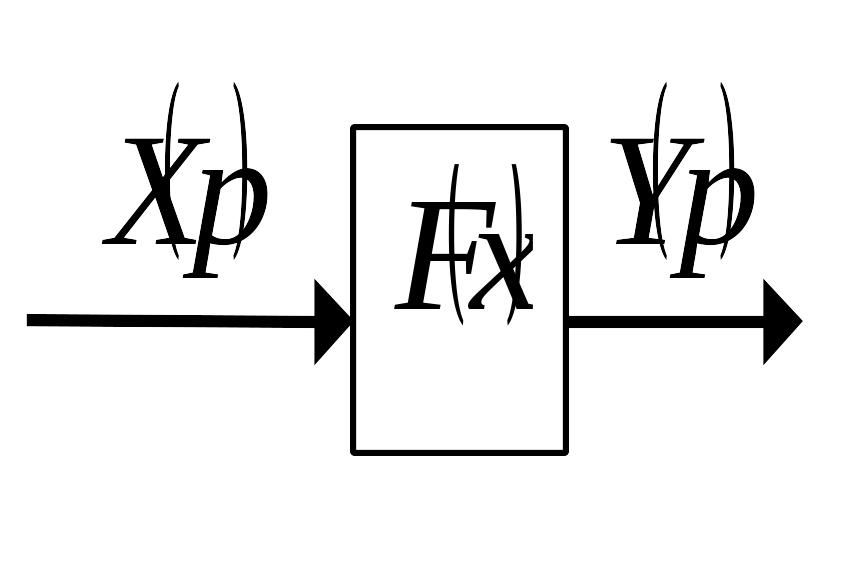
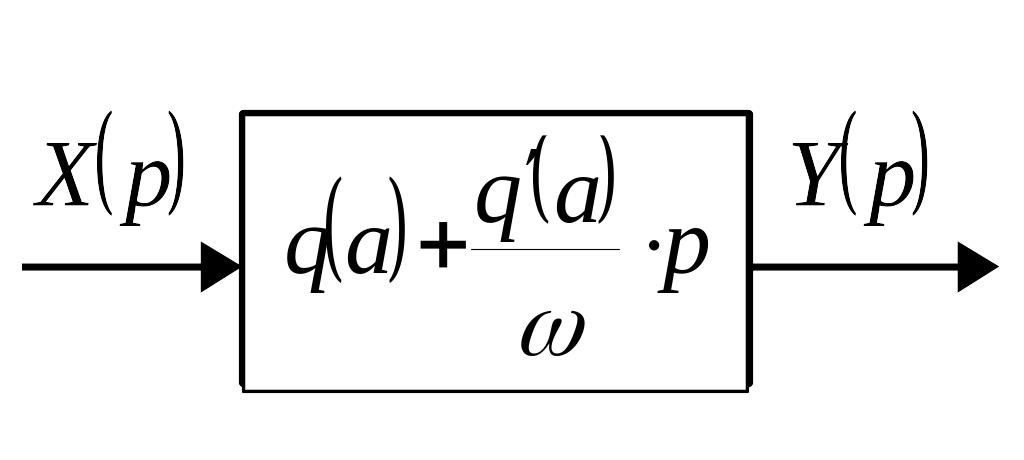
Гармонически линеаризованная периодическая функция нелинейного звена будет иметь вид

.

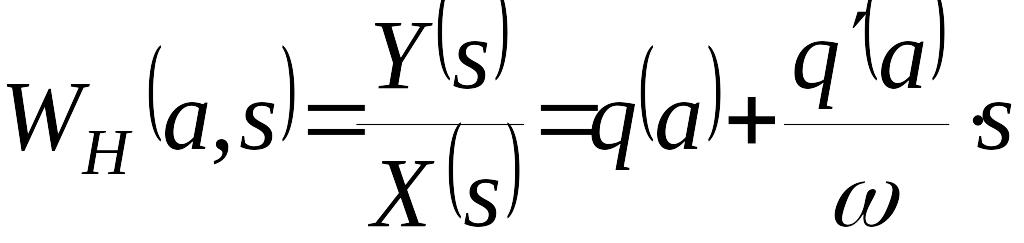Амплитудно-фазовая характеристика нелинейного гармонически линеаризованного звена получается в результате формальной перестановки и имеет вид . Следовательно, амплитудно-фазовая характеристика нелинейного звена зависит только от амплитуды гармонического сигнала и не зависит от его частоты (в противоположность характеристикам линейных звеньев).

Существуют нелинейности , для которых , и будут зависеть от амплитуды и частоты .

Из сказанного следует алгоритм исследования автоколебаний в нелинейных системах методом гармонической линеаризации.

Исследования автоколебаний в нелинейных системах методом гармонической линеаризации.

1. Структурную схему исследуемой системы автоматического управления приведем к виду

, ,

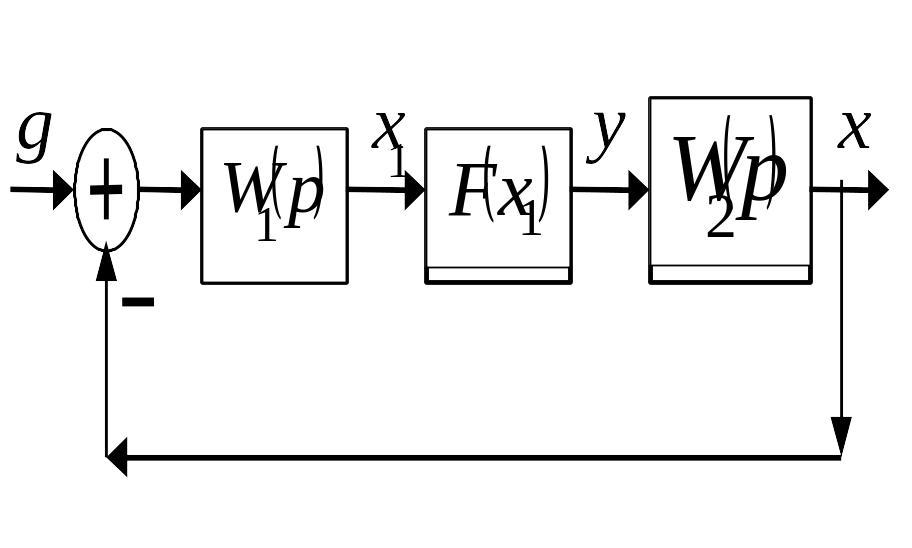
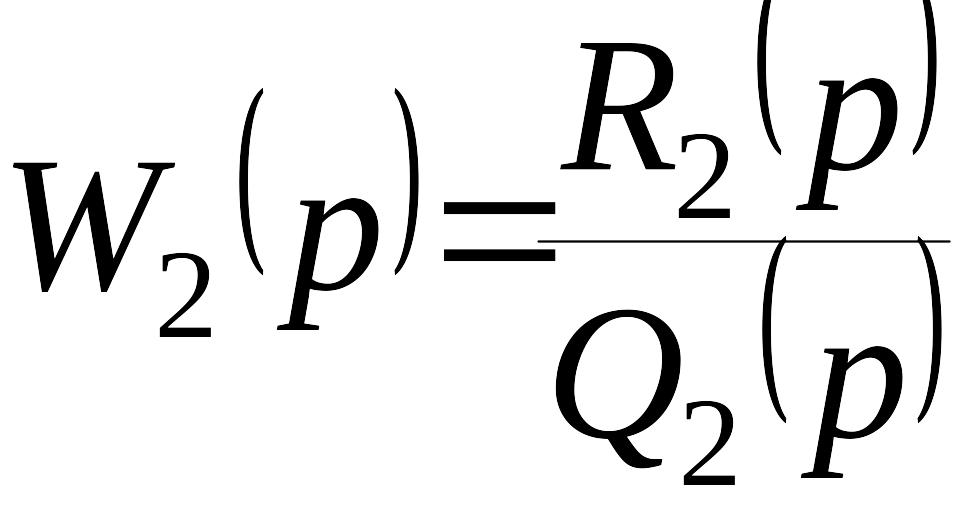– характеристика нелинейного звена системы управления.

2. Полагают: (условия применения метода гармонической линеаризации)

• в исследуемой системе управления возникают автоколебания с частотой и амплитудой .

• линейная часть системы обладает свойством фильтра.

Замечание: значения амплитуды и частоты автоколебаний пока неизвестны и подлежат определению.

3. Вычисляют коэффициенты гармонической линеаризации и по формулам

,

.

4. Исследуемую нелинейную систему заменяем гармонически линеаризованной системой, структурная схема которой имеет вид

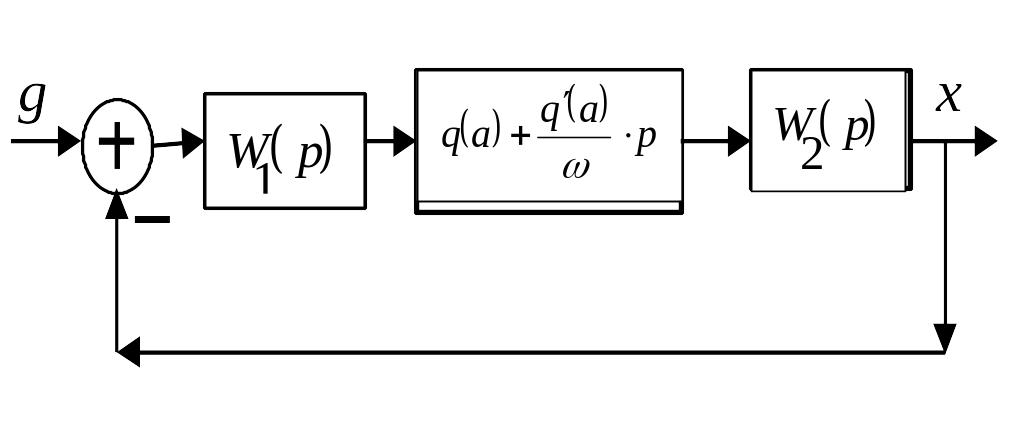
5. Определяют параметры периодического решения – амплитуду и – частоту.

6. Проводится анализ полученных результатов проверяются гипотезы пункта (2) исследуется устойчивость периодического решения, проводится моделирование процессов в системе на ЭВМ.