Математическая модель исследуемой системы автоматического управления.

В дальнейшем будем рассматривать системы автоматического управления любой сложности по структуре, но с одним нелинейным звеном, которое описывается уравнением вида . На структурных схемах нелинейное звено изображается следующим образом

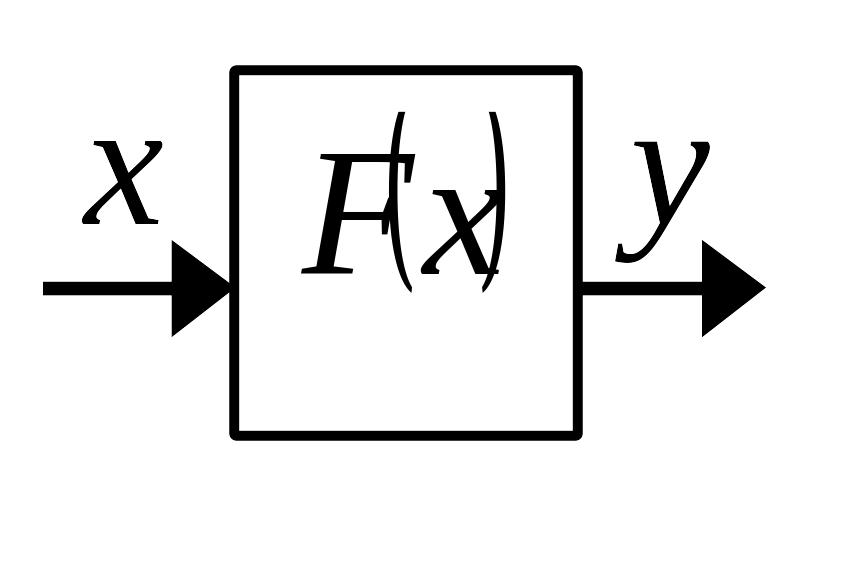
Будем полагать, что структурную схему системы управления можно преобразовать так, что будут выделены линейная часть системы и нелинейное звено в отдельные блоки, например, так как показано на рисунке. Линейная часть системы имеет передаточные функции

, ,

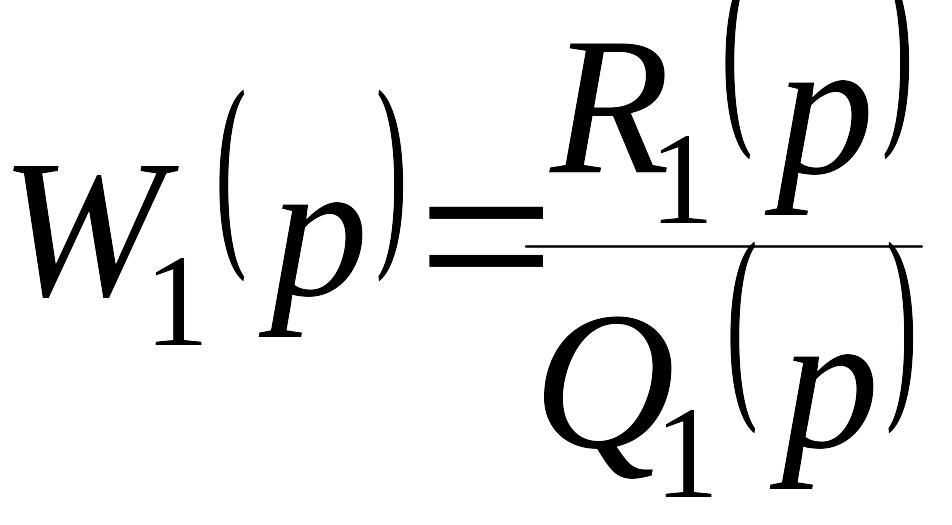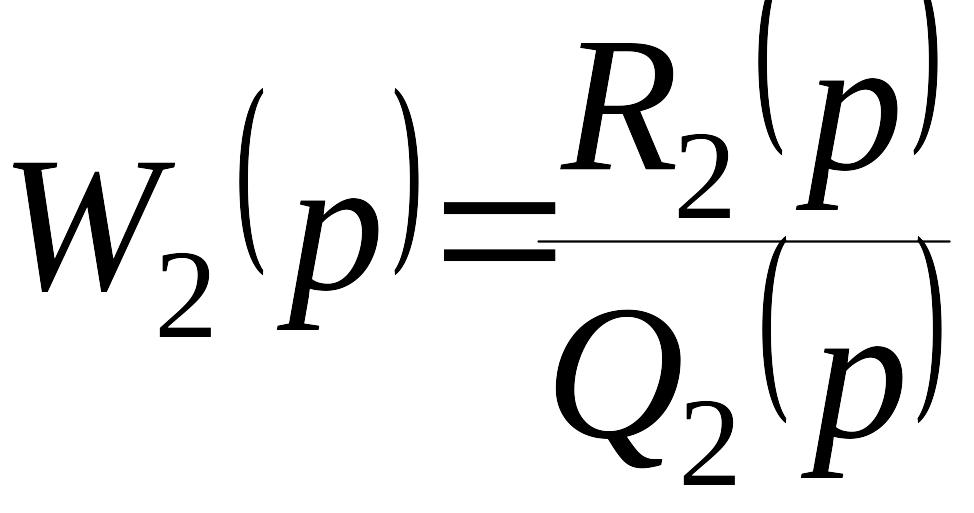где , , , – полиномы комплексной переменной , причем степень полинома меньше степени полинома , а степень полинома меньше степени полинома . Нелинейный элемент описывается уравнением .

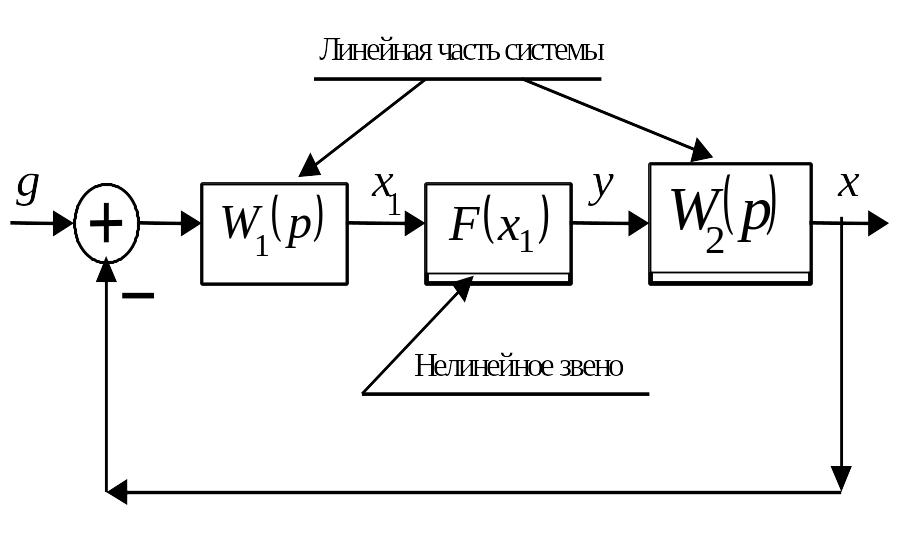
Будем считать, что , то есть исследуются соответственные движения системы. Рассматриваются установившиеся процессы в системе. Структурная схема системы приводится к виду.

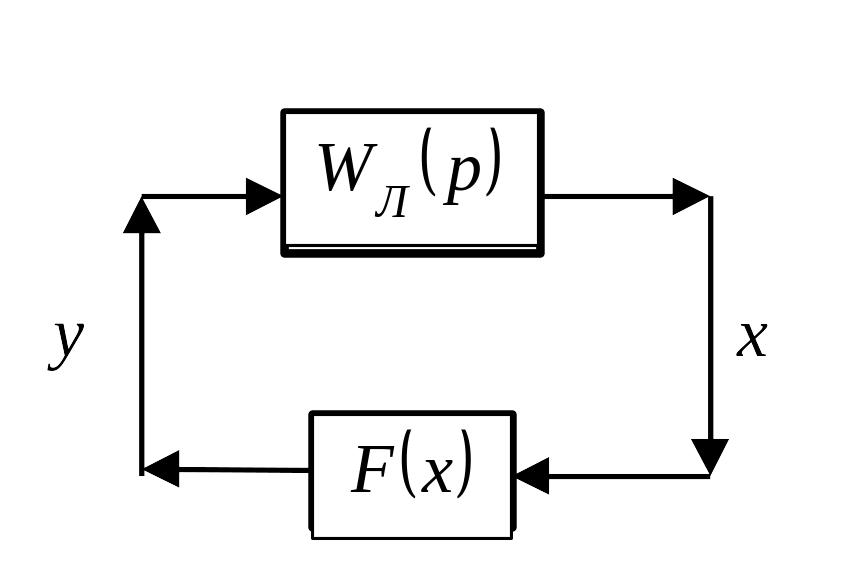
II. В системе возникли автоколебания.

(есть периодические решения у нелинейной математической модели системы).

Полагаем, что в исследуемой системе автоматического управления возникли автоколебания (есть периодические решения). Это соответствует тому, что на выходе системы возникает периодический сигнал (гармонический сигнал). Так как рассматриваются установившиеся движения системы, то можно считать, что на вход нелинейного звена поступает также гармонический сигнал амплитуды и частоты . Гармонический сигнал можно описать следующим образом . На выходе нелинейного звена получим сигнал .

Выполним графо-аналитический анализ сигнала на выходе нелинейного звена, когда на его вход поступает сигнал . В качестве нелинейного звена возьмем звено типа «люфт» или "зазор" (см. рисунок). На рисунке обозначено:

, при этом считается, что , ,

математическая модель нелинейного звена

, .

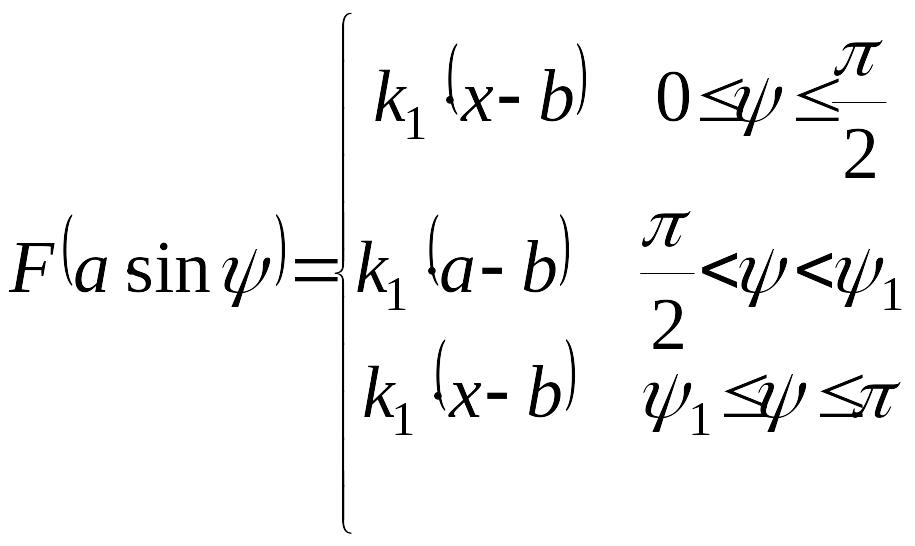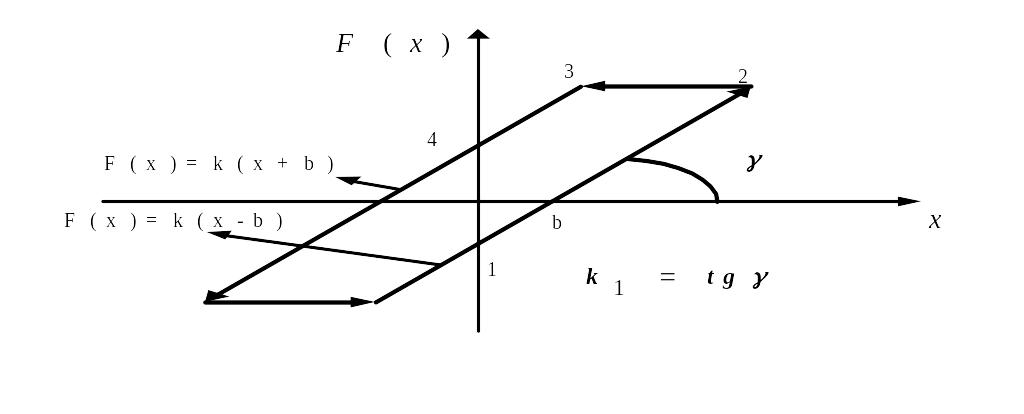
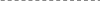
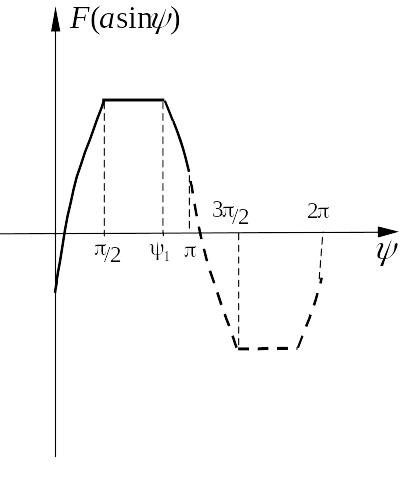
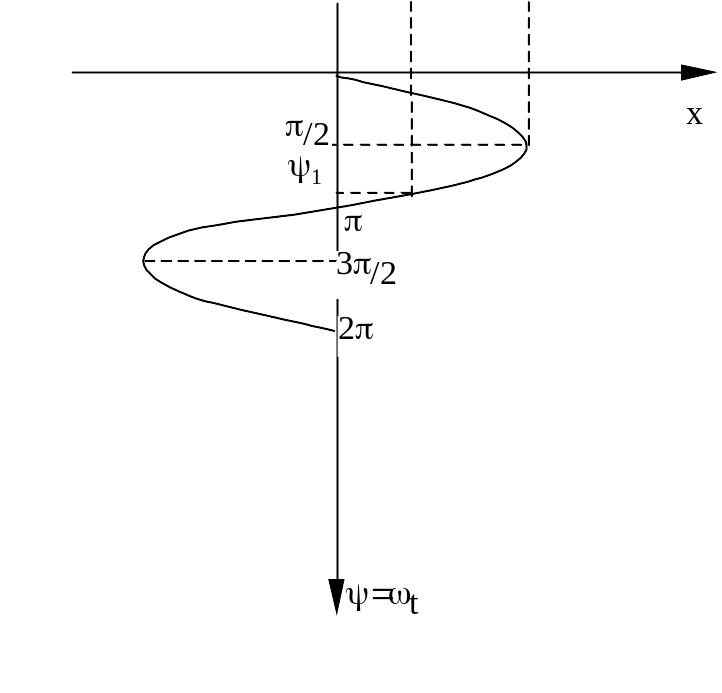
Из приведенных графиков следует. В случае возникновения автоколебаний в исследуемой системе с одним нелинейным звеном на выходе нелинейного звена возникает периодический сигнал с периодом 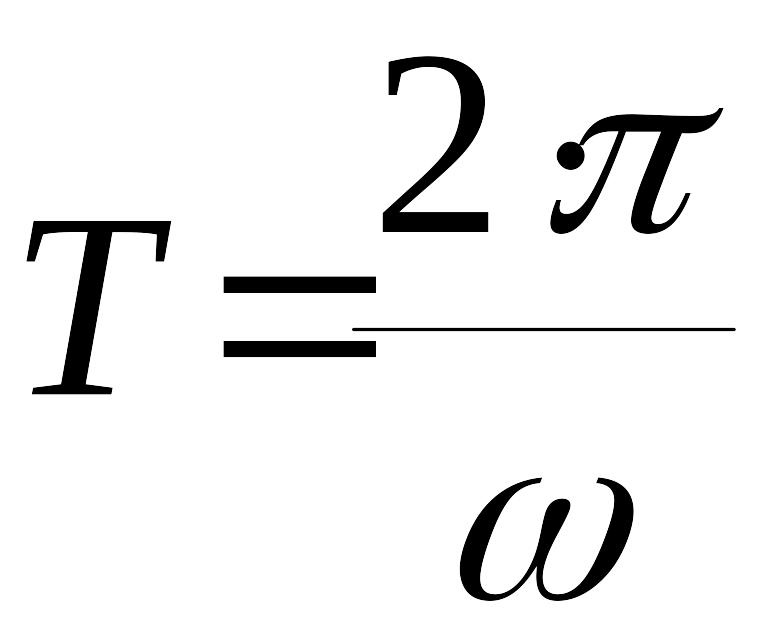. Период сигнала на выходе нелинейного звена совпадает с периодом сигнала на его выходе , .

4. Математическая основа метода гармонической линеаризации.

В случае гармонического сигнала на входе нелинейного звена системы управления на его выходе появляется периодический сигнал, период которого . Этот периодический сигнал на выходе нелинейного звена можно разложить в ряд Фурье

,

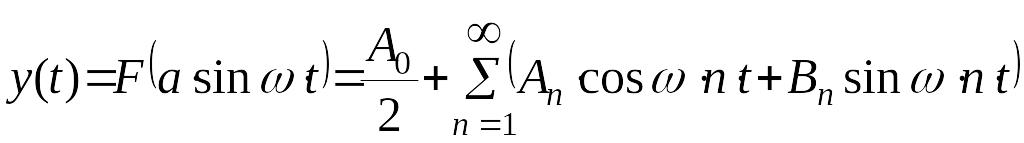где

,

,

,

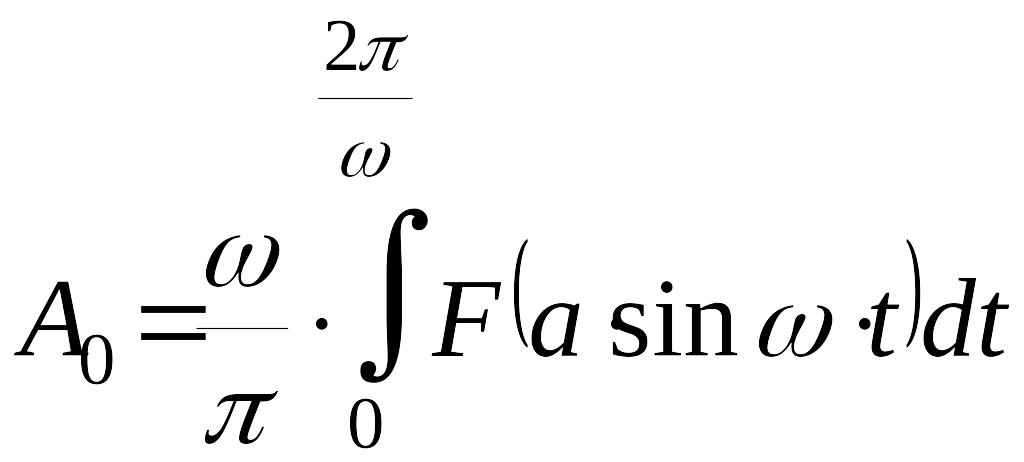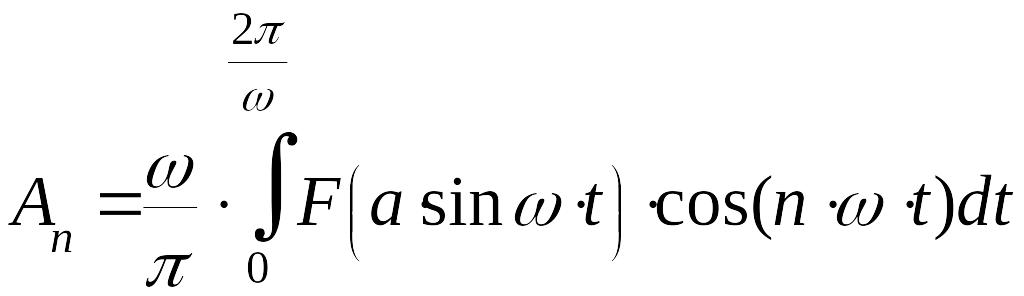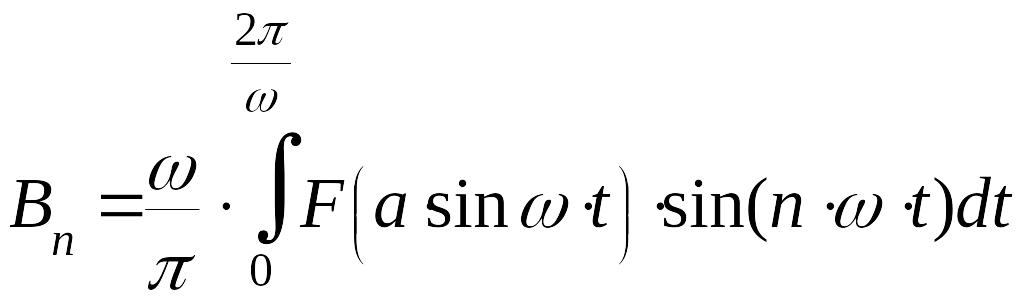где – частота -ой гармон

ики.

Если автоколебания в системе симметричны, то симметрична относительно оси абсцисс. Это значит и

.

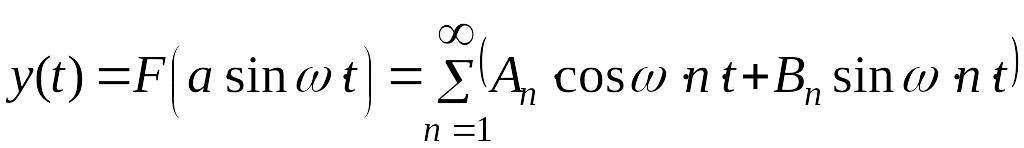4. Свойство фильтра линейной части системы.

Построим амплитудно–частотную характеристику линейной части системы. Пусть, например, она имеет вид, показанный на рисунке

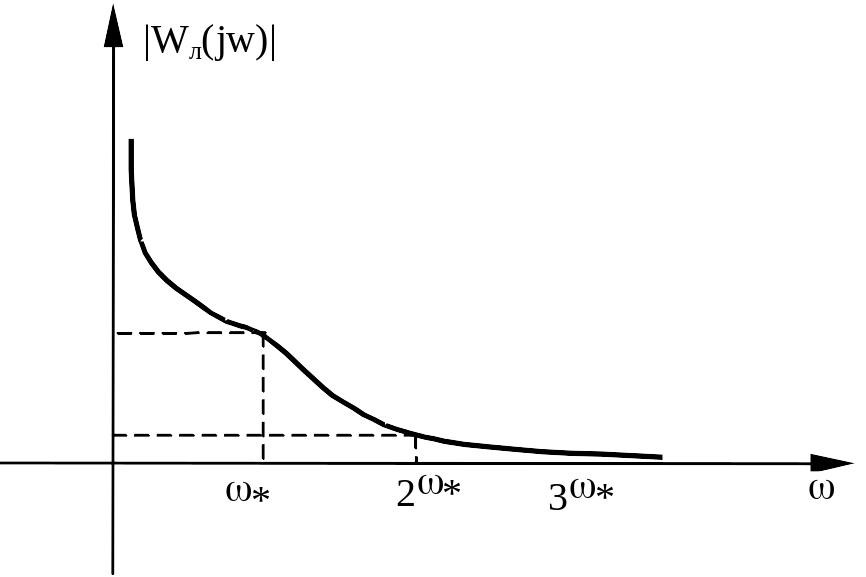
Отметим на оси частот частоту первой гармоники , возникших в системе автоколебаний, а затем и высшие гармоники , , … Предположим, что величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой, т.е. 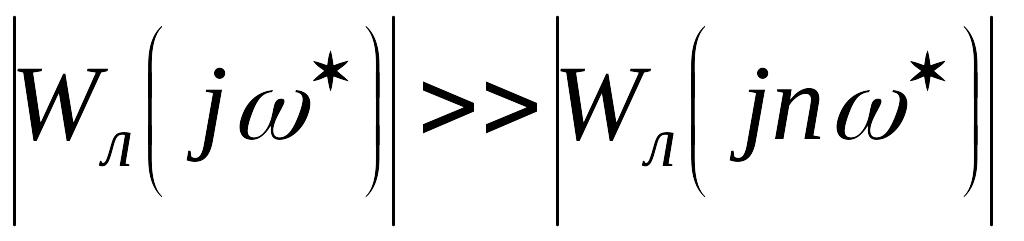, .Это положение называется свойством фильтра линейной части системы.

При наличии этого свойства фильтра линейной части – линейная часть системы будет хорошо пропускать первую гармонику нелинейных колебаний и слабо пропускать все высшие гармоники. Поэтому сигнал на выходе нелинейной системы (ее линейной части) будет близок к синусоидальному . Это обстоятельство усиливается и тем, что собственные амплитуды высших гармоник переменной , как правило, меньше, чем амплитуда первой гармоники.