Вывод 3. Уравнение движения системы вдоль линии переключения

или

.

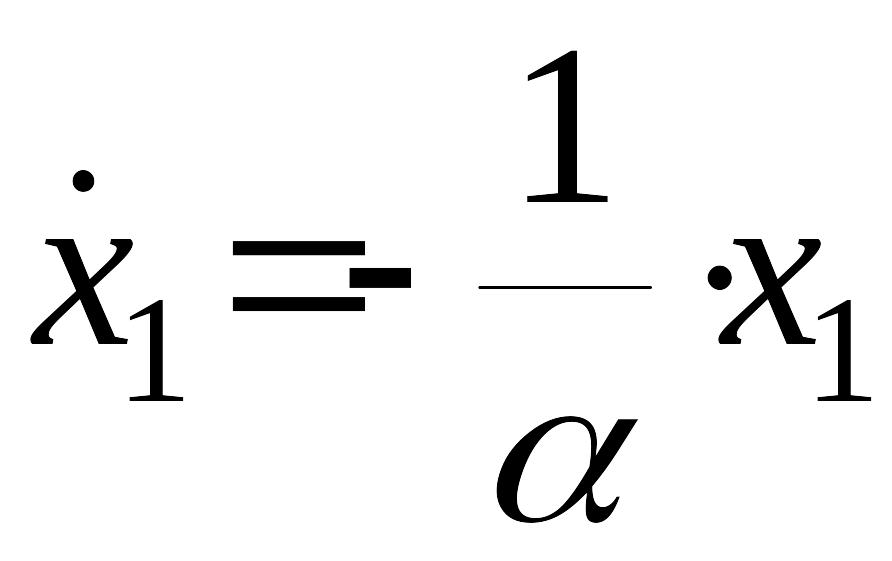Решение этого уравнения будет

,

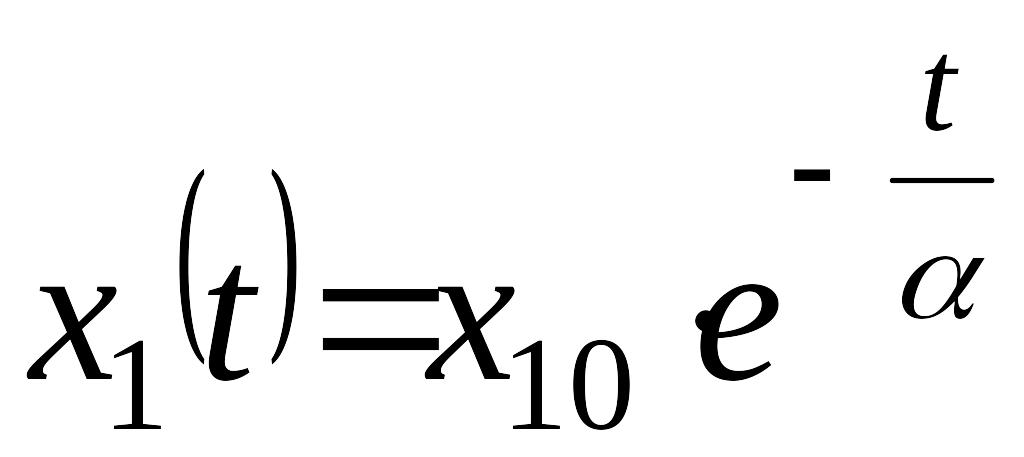где значения (начальное значение времени движения системы по линии переключения) и вычисляются в момент попадания изображающей точки на линию (отрезок) скольжения.

Скользящий процесс происходит по экспоненциальному закону и не зависит от параметров системы, а определяется только коэффициентом обратной связи. Нелинейная система второго порядка на участке скользящего режима вырождается в линейную систему первого порядка.

Найдем положение концов отрезка скользящего процесса и на фазовой плоскости. Очевидно, что в этих точках касательные к параболам совпадают с линией переключения. Это условие согласно уравнению (4)

можно записать в виде

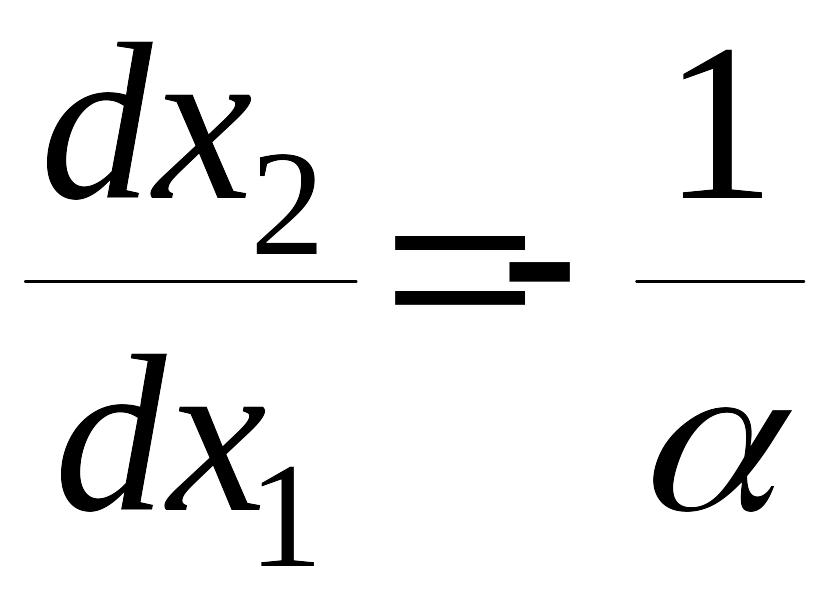. (9)

Тогда из уравнений траекторий (3) получим для точки условие в виде (приравнивая правые части равенств (5) и (9)):

; .

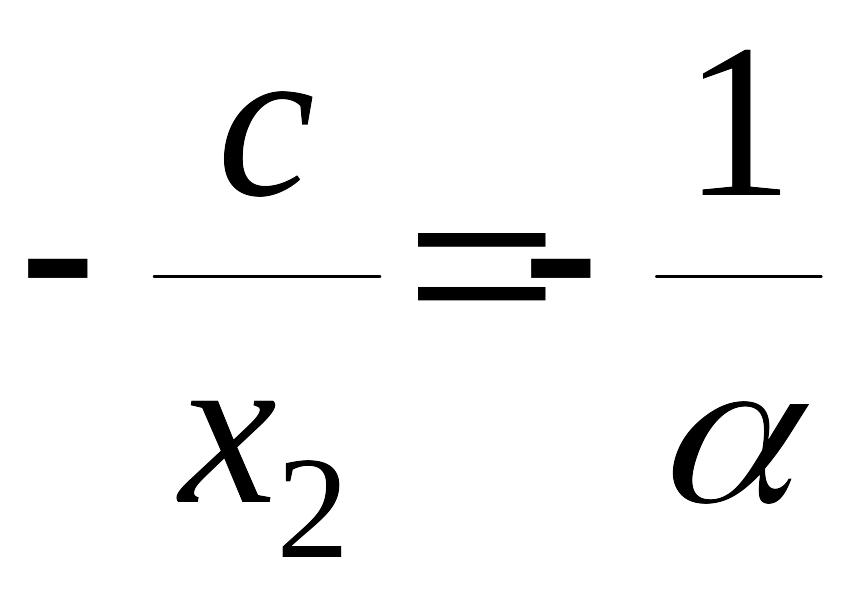Для точки (приравнивая правые части равенств (7) и (9):

; .

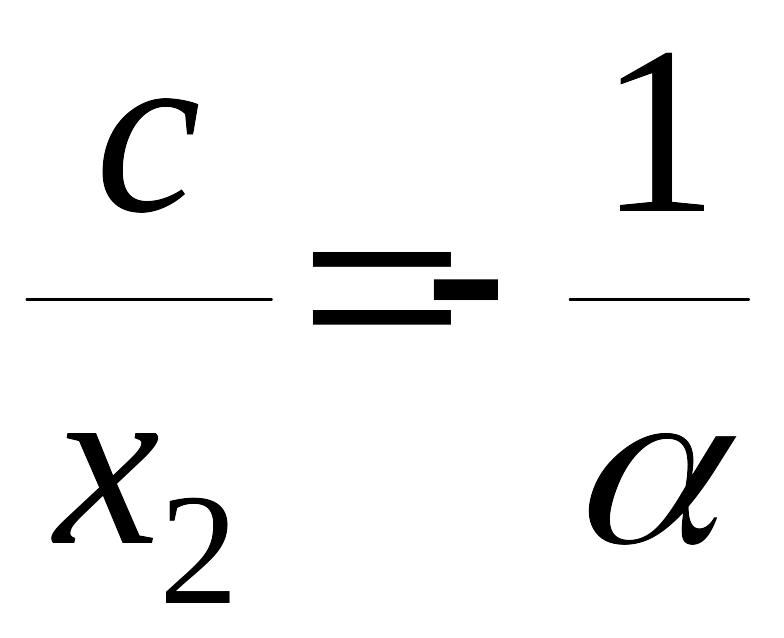Вывод 4. Отрезок скользящего процесса тем больше, чем больше коэффициент усиления обратной связи.

Процессы в релейных системах со скользящим режимом.

Пусть начальные условия таковы, что изображающая точка на фазовой плоскости занимает положение в области I. Здесь и дальнейшее движение изображающей точки происходит по фазовой траектории . В точке происходит переключение реле (изображающая точка достигла линии переключения). Далее изображающая точка перемещается по фазовой траектории . В точке изображающая точка достигает линии переключения внутри отрезка – отрезка скольжения. В этом случае как только фазовая траектория пересечет линию переключения (из области II в область I) вступит в свои права фазовая траектория из области I, которая вернет процесс на линию переключения внутри отрезка скольжения. Но тут вступает в свои права фазовая траектория из области II и т.д. В результате изображающая точка будет «скользить» по линии переключения к началу координат. Это соответствует переключениям релейного элемента с большой частотой. Теоретически частота вибраций бесконечна, а амплитуда вибраций равна нулю. Следовательно, теоретически, изображающая точка скользит по линии переключения к началу координат – равновесному состоянию. Фазовой траектории соответствует процесс во времени, показанный на рисунке, где отмечены те же характерные точки.

Лекция 9. Основы исследования систем автоматического управления методом гармонической линеаризации

В настоящее время метод гармонической линеаризации является одним из основных приближенных методов исследования нелинейных систем автоматического управления. Причины широкого применения в инженерной практике исследования нелинейных систем управления метода гармонической линеаризации состоит в том, что этот метод оказался способным в простейшем случае учитывать самые главные специфические свойства нелинейных систем (процессов) в зависимости от структуры и параметров системы высокого порядка. Этот метод удачно сочетает учет основных специфических нелинейных свойств системы, недоступных линейной теории, с возможностью применения хорошо разработанных в линейной теории управления расчетных приемов (с некоторой их модернизацией). Основное достоинство этого метода состоит в том, что он без рассмотрения переходного процесса позволяет непосредственно определить главные характеристики системы:

-основную частоту и фазу и амплитуду автоколебаний;

-их зависимость от формы нелинейности, структуры и параметров линейной части системы и от внешних воздействий; и т.п.;

Наряду с этим важное преимущество метода гармонической линеаризации заключается в возможности применения его к системам высокого порядка с любой сложностью линейных частей и с самыми разнообразными комбинациями мест включения нелинейных звеньев. Несмотря на приближенность метод гармонической линеаризации дает правильные для практических потребностей результаты получаются применительно ко многим классам систем.

Метод гармонической линеаризации позволяет:

1. Определить возможность возникновения автоколебаний в системе управления.

2. Вычислить параметры возникающих в системе автоколебаний: амплитуду и частоту.

3. Использовать для анализа процессов в нелинейных системах с некоторой модификацией хорошо разработанные методы линейной теории управления.

4. Учитывать самые главные, специфические свойства нелинейных систем.

5. Возможность применения его к исследованию систем высокого порядка и произвольной структуры.

Суть метода гармонической линеаризации состоит в замене нелинейного звена гармонически линеаризованным звеном, параметры которого в общем случае зависят от амплитуды и частоты сигнала на входе нелинейного звена.