3. Примеры решения задач

Пример 1. Тело вращается вокруг неподвижной оси по закону =A+Bt+Ct², где А = 10рад, В = 20рад/с, С = -2рад/с². Найти полное уско­рение точки, находящейся на расстоянии r = 0,1м от оси вращения, для момента времени t = 4с.

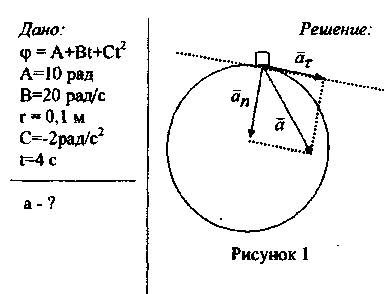
полное ускорение а точки, движущейся по кривой линии, может быть найдено как гео­метрическая сумма тан­генциального ускорения а_n, направленного к цен­ тру кривизны

траектории (см. рисунок 1).

, т.к. , то

. Тангенциальное и нормальное ускорения точек вращающегося тела выражаются формулами:

; ,

где - угловая скорость тела; - его угловое ускорение.

Тогда

Угловую скорость найдем, взяв первую производную от угла поворота по времени:

В момент времени t = 4с угловая скорость

[20+2(-2)4] рад/с = 4 рад/с.

Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:

= 2С = -4рад/ с².

Угловое ускорение не зависит от времени, т.е. постоянно. Подстав­ляя найденные значения и исходные данные, получим: = 1.65м/с².

Ответ: а = 1.65м/с².

Пример 2. Баллон содержит m₁= 80 г кислорода и m₂ = 320г аргона. Дав­ление смеси Р = 1 МПа, температура Т = 300 К. Принимая данные газа за идеальные, определить емкость баллона.

Решение:

По закону Дальтона, давление смеси равно cумме парциальных давлений газов, входящих в состав смеси.

По уравнению Менделеева-Клапейрона, парциальные давления кислорода Р₁ и аргона Р₂ выража­ется формулами:

Р₁= (m₁ / )(RT/V); P₂= (m₂ / ) (RT/V).

Следовательно, по закону Дальтона, давление смеси газов

Р= Р₁+Р₂ или Р = (m₁ / + m₂ / )(RT/V). Откуда ёмкость баллона

V= (m₁ / + m₂ / )(RT/Р), где R= 8,31 Дж/(моль К)

V = [(0,08/( 10^-3) + 0,32/(40 )) 8,31 /10⁶) = 0,0262 м³

Проверка размерностей:

Ответ: V = 0,0262 м³

Пример 3. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности по­тенциалов U₁ = 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емко­стью С₂ = 5 мкФ. Какая энергия израсходуется на образование искры в мо­мент присоединения второго конденсатора?

Решение:

Энергия W¹, израсходованная на образование искры, W¹=W₁-W₂, где W₁-энергия, которой обла­дал первый конденсатор до присоединения к нему второго конденсатора; W₂ - энергия, которую имеет батарея, составленная из первого и второго конден­саторов.

Энергия заряженного конденсатора определяется по формуле

W = CU²/2, где С - емкость конденсатора или батареи конденсаторов; U - разность потенциалов на обкладках

конденсаторов.

Тогда

W¹= C₁U₁²/2 - (C₁+C₂)U₂²/2, где C₁и С₂ - емкости первого и второго конденсаторов; U₁ - разность потенциалов, до которой был заряжен первый конденсатор; U₂ - разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора ос­тался прежний, выразим U₂:

U₂ = q/(C₁+C₂) = C₁U₁/(C₁+C₂).

Тогда

W¹=C₁U₁²/2 - ((С₁+С₂) С₁²U₁²)/(2(C₁+C₂)²)=1/2(C₁C₂/(C₁+C₂))U₁²

W¹=1/2(3 Дж.

[W¹] = (ФФ/Ф)В² = Дж.

Ответ: W¹= Дж.

4. ИНДИВИДУАЛЬНЫЕ СЕМЕСТРОВЫЕ ЗАДАНИЯ

4.1. КИНЕМАТИКА. ДИНАМИКА.

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Вариант 1

Задача 1. Тело брошено под углом а к горизонту с начальной скоростью . Определить максимальную высоту Н подъема тела над землей. Сопротивлением воздуха пренебречь.

Задача 2. Определить центростремительное ускорение точек земной поверхности на экваторе и на полюсе, вызванное суточным вращением Земли.

Задача 3 Автомобиль массой 4 т движется в гору с ускорением 0,2 м/с². Найти силу тяги, если уклон равен 0,02 и коэффициент сопротивления 0,04.

Задача 4. Динамометр, рассчитанный на 40 Н, имеет пружину с жесткостью к = 500 Н/м. Какую работу нужно совершить, чтобы растянуть пружину от середины шкалы до последнего деления?

Задача 5. С горки высотой h = 2 м и основание b = 5м съезжают санки, которые останавливаются, пройдя горизонтальный путь S = 35 м от основания горы. Найти коэффициент трения, считая его одинаковым на всем пути.

Задача 6. Мяч массой 400 г, брошенный вертикально вверх со скоростью 20 м/с, упал в ту же точку со скоростью 15 м/с. Найти работу силы сопротивления воздуха.

Задача 7. Двигатель мощностью 3 кВт за 12 с разогнал маховик до скорости вращения 10 об/с. Определить момент инерции маховика.

Задача 8. Шар скатывается с наклонной плоскости высотой 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатится с наклонной плоскости?

Задаче 9. Определить среднюю квадратичную скорость молекул кислорода при 20 °С. При какой температуре эта скорость равна 500 м/с?

Задача 10. Вычислить давление 1 моля молекул газа, занимающего при температуре 300 К объем 1л.

Задача 11. Углекислый газ массой 10 г нагрет от 20 до 30°С при постоянном давлении. Найти работу расширения газа и изменение его внутренней энергии.

Задача 12. Средняя длина свободного пробега молекул кислорода при нормальных условиях равна 10³ см. Вычислить среднюю арифметическую скорость молекул и число соударений в секунду.

Задача 13. Какой радиус должен иметь проводящий шар, чтобы его

емкость в вакууме равнялась 1 фараде?

Задача 14. Площадь пластины слюдяного конденсатора 36 см², толщина слоя диэлектрика 0,14 см. Вычислить емкость, заряд и энергию конденсатора, если разность потенциалов нашего обкладках 3 В, а относительная диэлектрическая проницаемость слюды

Задача 15. По проводнику сечением 1,5 мм² течет ток 0,3 А. Считая концентрацию свободных электронов в веществе равной 10²⁸ м³.

Определить среднюю скорость упорядоченного движения свободных электронов.

Задача 16. Определить падение напряжения в линии электропередачи длиной 506 м при токе в ней в 15 А. Проводка - алюминиевой провод сечением 14 мм².