3.3. Системы линейных ду с постоянными коэффициентами
Рассмотрим еще один метод интегрирования нормальной системы уравнений (3.1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т. е. систему вида
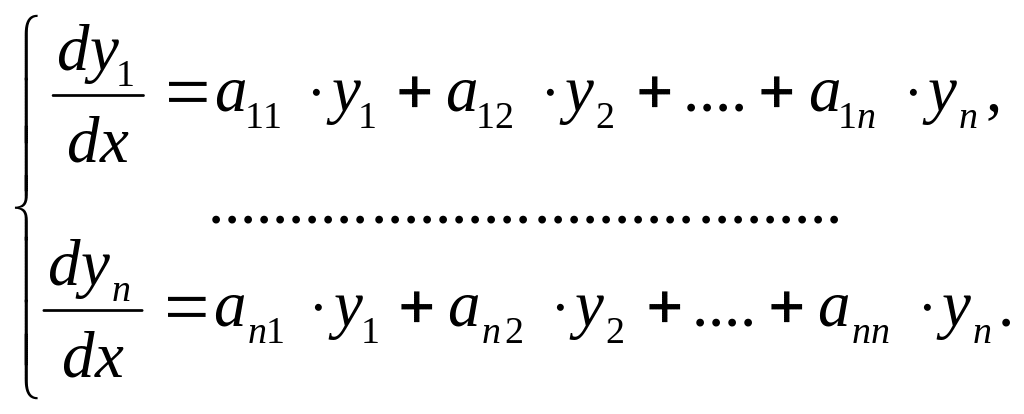
Для простоты ограничимся рассмотрением
системы трех уравнений с тремя неизвестными
функциями
,
и
:
(3.6)
где все коэффициенты
- постоянные. Будем искать частное
решение системы (3.6) в виде
,
,
,
(3.7)
где
- постоянные, которые надо подобрать
(найти) так, чтобы функции (3.7) удовлетворяли
системе (3.6).
Подставив эти функции в систему (3.6) и
сократив на множитель
,
получим:
или
(3.8)
Систему (3.8) можно рассматривать как
однородную систему трех алгебраических
уравнений с тремя неизвестными
.
Чтобы эта система имела ненулевое
решение, необходимо и достаточно, чтобы
определитель системы был равен нулю:
. (3.9)
Уравнение (3.9) называется характеристическим уравнением системы (3.6). Раскрыв определитель, получим уравнение третьей степени относительно . Рассмотрим возможные случаи.
Случай 1. Корни характеристического
уравнения действительны и различны:
.
Для каждого корня
(i
= 1,2,3) напишем систему (3.8) и определим
коэффициенты
(один из коэффициентов можно считать
равным единице). Таким образом, получаем:
для корня
частное решение системы (3.6):
,
,
;
для корня
,
,
;
для корня
,
,
.
Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (3.6) записывается в виде
,
,
.
Пример 3.3. Решить систему уравнений:
Решение: Характеристическое уравнение (3.9) данной системы имеет вид
,
или 
,
,
,
.
Частные решения данной системы ищем в виде
, ,
, .
Найдем
и
.
При
система (3.8) имеет вид
т.е.
Эта система имеет бесчисленное множество
решений. Положим
,
тогда
.
Получаем частные решения
,
и
.
При система (3.8) имеет вид
Положим
,
тогда
.
Значит, корню
соответствуют частные решения:
,
и
.
Общее решение исходной системы, согласно формуле (3.10), запишется в виде:
, 
.
Случай 2. Корни характеристического
уравнения различные, но среди них есть
комплексные:
,
,
.
Вид частных решений в этой ситуации определяют так же, как и в случае 1.
Замечание. Вместо полученных частных
решений можно взять их линейные комбинации
(п. 3.6, случай 3), применяя формулы Эйлера;
в результате получим два действительных
решения, содержащих функции вида
,
.
Или, выделяя действительные и мнимые
части в найденных комплексных частных
решениях, получим два действительных
частных решения (можно показать, что
они тоже являются решениями уравнения).
При этом понятно, что комплексно-сопряженный
корень
не даст новых линейно независимых
действительных решений.
Пример 3.4. Найти частное решение системы
удовлетворяющее начальным условиям:
,
,
.
Решение: Составляем и решаем характеристическое уравнение:
,
,
,
,
, 
, 
.
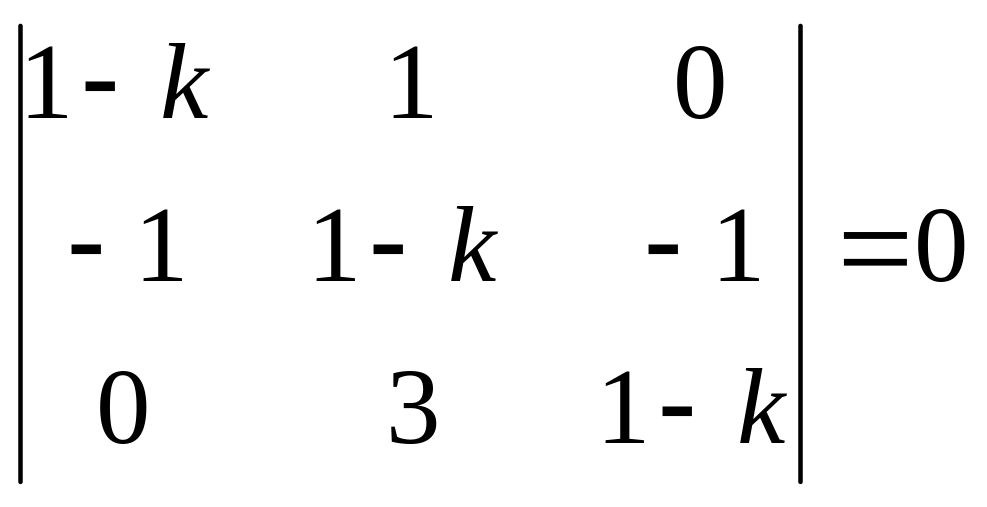Для получаем:
(см.
(3.8)). Отсюда находим:
,
(положили),
.
Частное решение системы:
,
,
.
Для
получаем (см. (3.8)):
Отсюда находим:
(положили),
,
.
Частное комплексное решение системы:
,
,
.
В найденных решениях выделим действительную (Re) и мнимую (Im) части:
,
,
;
,
,
;
,
,
.
Как уже отмечено, корень
приведет к этим же самым решения. Таким
образом, общее решение системы имеет
вид
,
,
.
Выделим частное решение системы. При
заданных начальных условиях получаем
систему уравнений для определения
постоянных
:
,
,
.
Следовательно, искомое частное решение имеет вид
,
,
.
Случай 3. Характеристическое уравнение имеет корень кратности m (m = 2,3). Решение системы, соответствующее кратному корню, следует искать в виде:
а) если m = 2, то
,
,
;
б) если т = 3, то
,
,
.
Это решение зависит от m произвольных постоянных. Постоянные А, В, С,...,N определяются методом неопределенных коэффициентов. Выразив все коэффициенты через m, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим m линейно независимых частных решений системы (3.6).
Пример 3.5. Решить систему уравнений:
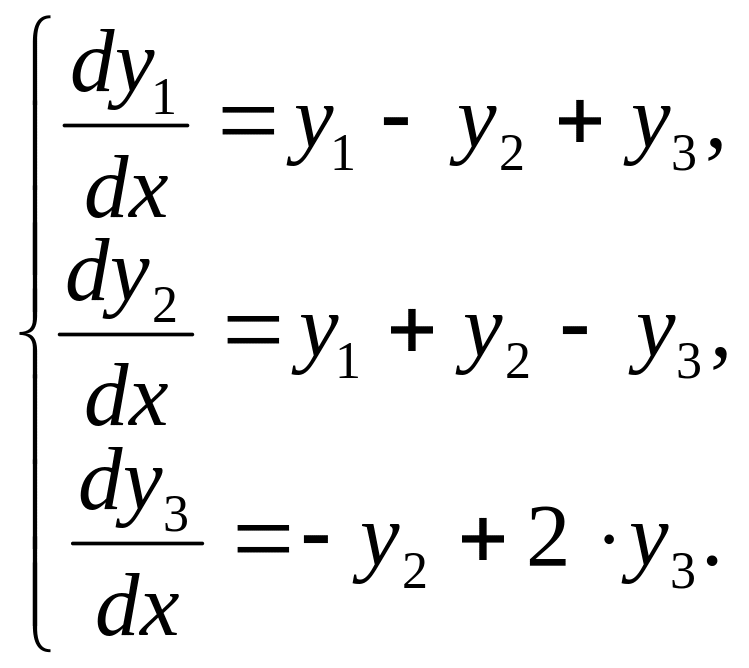
Решение: Составляем и решаем характеристическое уравнение
,
,
.
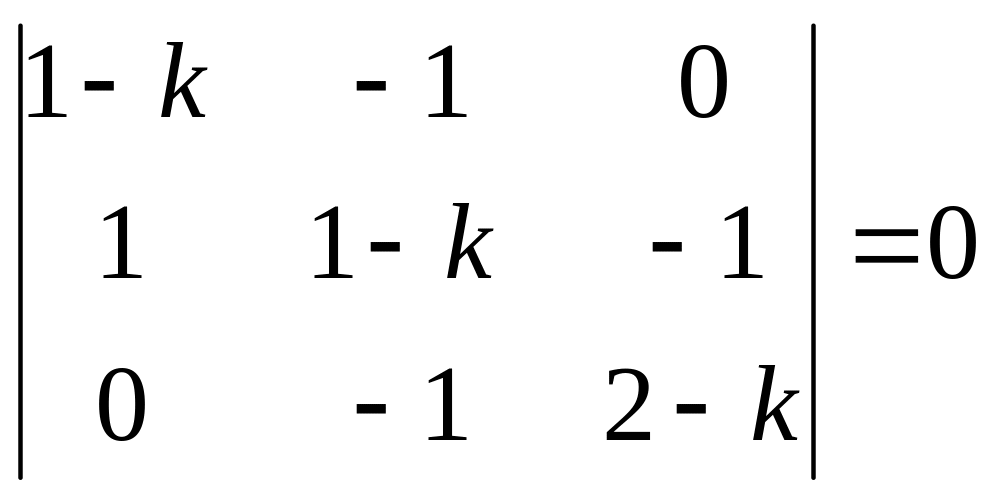Корню соответствует система (см. (3.8)):
Полагая
,
находим
.
Получаем одно частное решение исходной
системы:
,
,
.
Двукратному корню
(m = 2) соответствует
решение вида
,
,
.
Подставляем эти выражения (решения) в уравнения исходной системы:
или, после сокращения на
и группировки,
Эти равенства тождественно выполняются лишь в случае, когда
Выразим все коэффициенты через два из них (т = 2), например через А и В. Из второго уравнения имеем F = В. Тогда, с учетом первого уравнения, получаем D = В. Из четвертого уравнения находим Е = А - D, т. е. Е = А - В. Из третьего уравнения: С = Е — В, т. е. С = А - В - В, или С = А - 2∙В. Коэффициенты А и В - произвольные.
Полагая А = 1, В = 0, находим: С = 1, D = 0, Е = 1, F = 0.
Полагая А = 0, В = 1, находим: С = - 2, D = 1, Е = - 1, F = 1.
Получаем два линейно независимых частных
решения, соответствующих двукратному
корню
:
,
,
и
,
,
.
Записываем общее решение исходной системы:
,
,
.