1.5. Линейные однородные ду n-го порядка

Полученные результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид

. (1.18)

1. Если функции , ,…., , являются частными решениями уравнения (1.18), то его решением является и функция .

2. Функции называются линейно независимыми на , если равенство выполняется лишь в случае, когда все числа ; в противном случае (если хотя бы одно из чисел не равно нулю) функции - линейно зависимы.

3. Определитель Вронского имеет вид

.

4. Частные решения уравнения (1.18) образуют фундаментальную систему решений на , если ни в одной точке этого интервала вронскиан не обращается в нуль, т. е. для всех .

5. Общее решение ЛОДУ (1.18) имеет вид ,

где - произвольные постоянные, - частные решения уравнения (1.18), образующие фундаментальную систему.

Пример 1.6. Показать, что функции , , образуют фундаментальную систему решений некоторого ЛОДУ третьего порядка (дополнительно: составить это уравнение).

Решение: Найдем W(x):

.

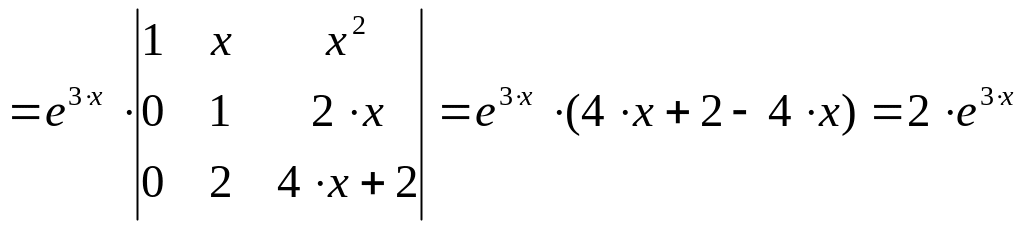Ясно, что для всех . Следовательно, данные функции образуют фундаментальную систему решений ЛОДУ третьего порядка. В общем виде ЛОДУ третьего порядка выглядит так:

.

Подставив функции в это уравнение, получим систему из трех уравнений относительно функций , , . Решая ее, получим ЛОДУ ; его общее решение:

.

1.6. Интегрирование лоду второго порядка с постоянными коэффициентами

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка:

, (1.19)

где р и q постоянны.

Для нахождения общего решения уравнения (1.19) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 1.5).

Будем искать частные решения уравнения (1.19) в виде

,

где k — некоторое число (предложено Л. Эйлером). Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение (1.19), получим:

, т. е.

, или ( ). (1.20)

Уравнение (1.20) называется характеристическим уравнением ДУ (1.19) (для его составления достаточно в уравнении (1.19) заменить у", у' и у соответственно на k² , k и 1).

При решении характеристического уравнения (1.20) возможны следующие три случая.

Случай 1. Корни и уравнения (1.20) действительные и различные:

.

В этом случае частными решениями уравнения (1.19) являются функции и . Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан

.

Следовательно, общее решение уравнения (1.19), согласно формуле (1.16), имеет вид

. (1.21)

Пример 1.7. Решить уравнение у" - 5·у' + 6·у = 0.

Решение: Составим характеристическое уравнение: . Решаем его: , . Записываем общее решение данного уравнения: , где и - произвольные постоянные (формула (1.21)).

Случай 2. Корни и уравнения (1.20) действительные и равные:

, .

В этом случае имеем лишь одно частное решение . Покажем, что наряду с решением уравнения (1.19) будет и . Действительно, подставим функцию в уравнение (1.19). Имеем:

.

Но , т. к. есть корень уравнения (4.2); , т. к. по условию .

Поэтому , т. е. функция является решением уравнения (1.19).

Частные решения , образуют фундаментальную систему решений: . Следовательно, в этом случае общее решение ЛОДУ (1.19) имеет вид

. (1.22)

Случай 3. Корни и уравнения (1.20) комплексные: , .

.

В этом случае частными решениями уравнения (1.19) являются функции и По формулам Эйлера (см. Часть 1, п. 27.3)

,

имеем:

,

.

Найдем два действительных частных решения уравнения (1.19). Для этого составим две линейные комбинации решений и :

и .

Функции и являются решениями уравнения (1.19), что следует из свойств решений ЛОДУ второго порядка (см. теорему 1.2). Эти решения и образуют фундаментальную систему решений, так как (убедитесь самостоятельно!). Поэтому общее решение уравнения (4.1) запишется в виде , или

. (1.23)

Пример 1.8. Решить уравнение у" - 6у' + 25у = 0.

Решение: Имеем: k² – 6k + 25 = 0, , . По формуле (1.23) получаем общее решение уравнения:

.

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (1.19) сводится к нахождению корней характеристического уравнения (1.20) и использованию формул (1.21)-(1.23) общего решения уравнения (не прибегая к вычислению интегралов).