9. Некоторые приложения степенных рядов

9.1. Приближённые вычисления значений функции.

Пусть требуется вычислить значение функции при с заданной точностью .

Если функцию в интервале можно разложить в степенной ряд

и , то точное значение равно сумме этого ряда при т. е.

,

а приближенное значение, - частичной сумме , т.е.

.

Точность этого равенства увеличивается с ростом п. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т. е.

,

где

Таким образом, ошибку можно найти, оценив остаток ряда.

Для рядов лейбницевского типа

(см. п. 6.1).

В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммировался. В качестве оценки берут величину остатка этого нового ряда.

Пример 9.1. Найти sin 1 с точностью до 0,001.

Решение: Согласно формуле (8.5),

.

Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как а , то для нахождения sin 1 с точностью до 0,001 достаточно первых трех слагаемых:

.

Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin 1 примерно равно 0,84147.

Пример 9.2. Вычислить число с точностью до 0,001.

Решение: Подставляя х = 1 в формулу (8.4), получим:

Справа стоит знакоположительный ряд. Возьмем п слагаемых и оценим ошибку :

,

т.е. . Остается подобрать наименьшее натуральное число п, чтобы выполнялось неравенство .

Нетрудно вычислить, что это неравенство выполняется при . Поэтому имеем:

.

Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена

,

где с находится между 0 и . В последнем примере , . Так как , то . При имеем:

, .

9.2. Приближенное вычисление определенных интегралов

Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции (см. [1] р.7 или [2] р.4), либо нахождение первообразной сложно.

Пусть требуется вычислить с точностью до . Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости включит в себя отрезок , то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.

Пример 9.3. Вычислить интеграл с точностью до .

Решение: Разложим подынтегральную функцию в ряд Маклорена, заменяя х на (-х²) в формуле (8.4):

, . (9.1)

Интегрируя обе части равенства (9.1) на отрезке , лежащем внутри интервала сходимости , получим:

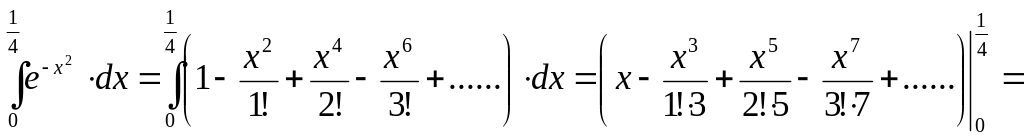
Получили ряд лейбницевского типа. Так как , а ,

то с точностью до 0,001 имеем:

.

Замечание. Первообразную F(x) для функции легко найти в виде степенного ряда, проинтегрировав равенство (9.1) в пределах от 0 до х:

, .

Функции и играют очень важную роль в теории вероятностей. Первая - плотность стандартного распределения вероятностей, вторая - функция Лапласа (или интеграл вероятностей). Мы получили, что функция Лапласа представляется рядом

,

который сходится на всей числовой оси.