7.2. Сходимость степенных рядов. Теорема н.Абеля
Выясним вопрос о сходимости степенного ряда (7.3).
Область сходимости степенного ряда
(7.3) содержит, по крайней мере, одну точку:
(ряд (7.4) сходится в точке
).
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.
Теорема 7.1 (Абель). Если степенной
ряд (7.3) сходится при
,
то он абсолютно сходится при всех
значениях х,
удовлетворяющих неравенству
.
По условию ряд
сходится.
Следовательно, по необходимому
признаку сходимости
.
Отсюда следует, что величина
ограничена, т. е. найдется такое число
М > 0, что для всех n
выполняется неравенство
,
Пусть
,
тогда величина
и, следовательно,
,
,
т. е. модуль каждого члена ряда (7.3) не превосходит соответствующего члена сходящегося (q < 1) ряда геометрической прогрессии. Поэтому по признаку сравнения при ряд (7.3) абсолютно сходящийся.
Следствие 7.1.
Если ряд (7.3) расходится при
,
то он расходится и при всех х,
удовлетворяющих неравенству
.
Действительно, если допустить сходимость
ряда в точке
,
для которой
,
то по теореме Абеля ряд сходится при
всех х, для которых
и, в частности, в точке
,
что противоречит условию.
7.3. Интервал и радиус сходимости степенного ряда
Из теоремы Абеля следует, что если
есть точка сходимости степенного ряда,
то интервал
весь состоит из точек сходимости данного
ряда; при всех значениях х вне
этого интервала ряд (7.3) расходится.
-R
+R
Ряд
сходится
0
-׀x0׀
׀x0׀
Ряд расходится Ряд расходится
Рис. 3
Интервал
и называют интервалом сходимости
степенного ряда. Положив
,
интервал сходимости можно записать в
виде (-R;R).
Число R называют радиусом
сходимости степенного ряда, т. е.
R > 0 — это такое число,
что при всех х,
для которых
,
ряд (7.3) абсолютно сходится, а при
ряд расходится (см. рис.3).
В частности, когда ряд (7.3) сходится
лишь в одной точке
,
то считаем, что R = 0. Если
же ряд (7.3) сходится при всех значениях
(т. е. во всех точках числовой оси), то
считаем, что
.
Отметим, что на концах интервала
сходимости (т.е. при
и при
)
сходимость ряда проверяется в каждом
случае отдельно.
Для нахождения радиуса сходимости степенного ряда (7.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
и применим к нему признак Даламбера. Допустим, что существует предел
,
.
По признаку Даламбера ряд сходится,
если
,
т.е. ряд сходится при тех значениях
х, для
которых
;
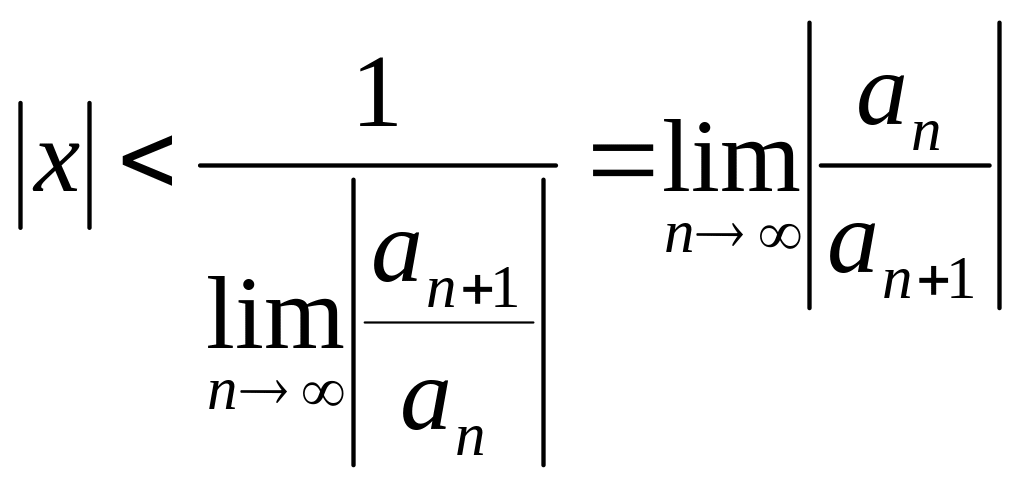ряд, составленный из модулей членов
ряда (7.3), расходится при тех значениях
х, для
которых
.
Таким образом, для ряда (7.3) радиус абсолютной сходимости
. (7.5)
Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что
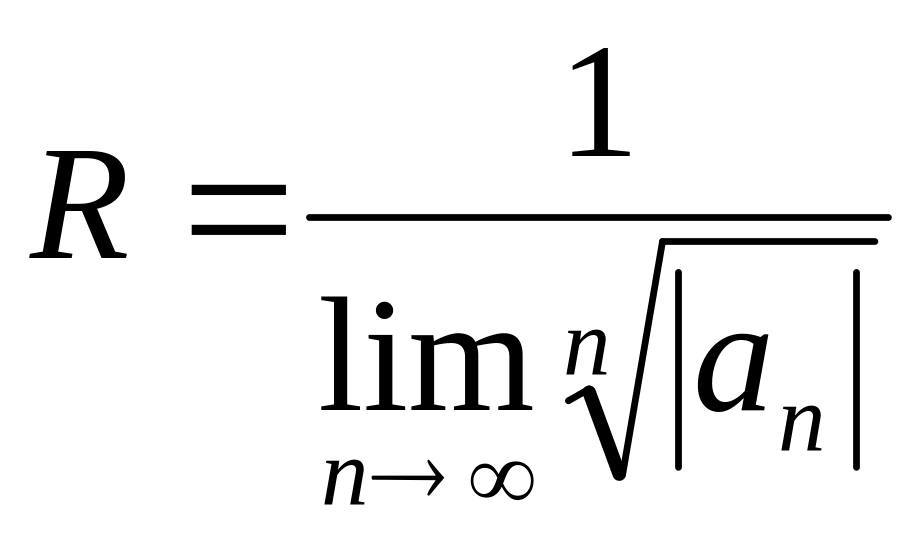. (7.6)
Замечания.
1. Если
,
то можно убедиться, что ряд (7.3) абсолютно
сходится на всей числовой оси. В этом
случае
.
Если
,
то
.
2. Интервал сходимости степенного ряда
(7.4) находят из неравенства
;
и он имеет вид
.
3. Если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (7.5) и (7.6)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
Пример 7.3. Найти область сходимости
ряда
.
Решение: Воспользуемся формулой (7.5):
.
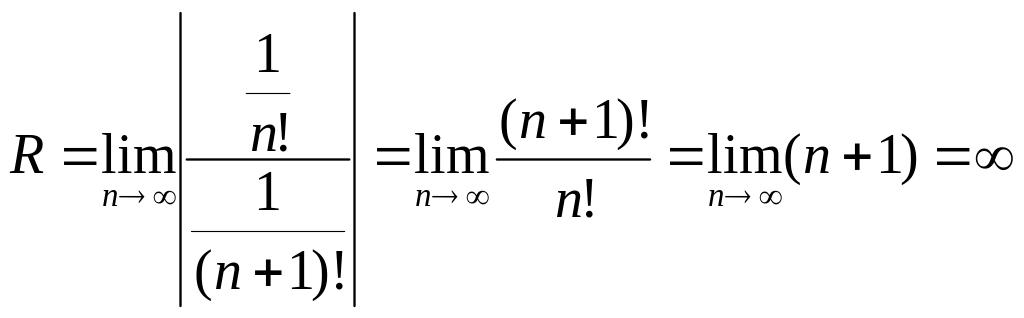Следовательно, данный ряд абсолютно сходится на всей числовой оси.
Пример 7.4. Найти область сходимости ряда
Решение: Данный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:
,
,
.
Ряд абсолютно сходится, если
или
.
Исследуем поведение ряда на концах
интервала сходимости.
При
имеем ряд
,
который сходится по признаку Лейбница.
При
имеем ряд
- это тоже сходящийся Лейбницевский
ряд. Следовательно областью сходимости
исходного ряда является отрезок
.
Пример 7.5. Найти область сходимости ряда:
.
Решение: Находим радиус сходимости ряда по формуле (7.5):
.
Следовательно, ряд сходится при
,
т.е. при
.
При
имеем ряд
,
который сходится по признаку Лейбница.
При имеем расходящийся ряд
.
Следовательно, областью сходимости
исходного ряда является полуотрезок
.