2. Приклади визначення пропускної здатності транспортної мережі.

В загальному випадку визначення практичної пропускної здатності з позицій вірогідно-статистичного підходу за формулою (2) аналітично ускладнено, і тому, практично єдиний надійний спосіб її визначення – імітаційне моделювання. Але для деяких типових і достатньо поширених випадків використовуються аналітичні формули практичної пропускної здатності.

Випадок 1. Термін обслуговування транспортної одиниці описується нормальним законом розподілу, T_р – детермінована величина.

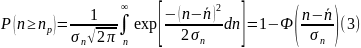
де – середнє значення пропускної здатності визначається за формулою (1); – середнє квадратичне відхилення пропускної здатності елементів системи:

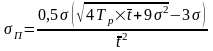, (4)

де 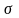- середньоквадратичне відхилення часу обслуговування транспортної одиниці, год.

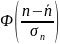– табульований інтеграл вірогідності.

Розрахункова пропускна здатність транспортної системи:

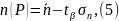
де - числове значення стандартизованого відхилення інтегральної функції нормального закону розподілу: приймається в залежності від прийнятого рівня довірчої вірогідності, для більшості практичних задач автомобільного транспорту Р=0,95 і =1,96.

Випадок 2. Час розрахункового періоду 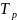і час обслуговування розподілені по нормальному закону і не піддавались кореляції. По формулі 2:

де 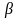- відношення середньоквадратичного відхилення часу розрахункового періоду до середньоквадратичного відхилення часу обслуговування транспортної одиниці, тобто:

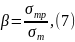
де 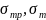– середнє квадратичне відхилення відповідно тривалості розрахункового періоду і обслуговування транспортної одиниці.

Функція розподілу коливань пропускної здатності транспортної системи:

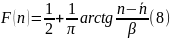
Вірогідність того, що дійсне значення пропускної здатності буде не менш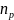е , складе:

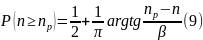
де – вірогідність того, що система на протязі проміжку часу обслужить не меншу кількість транспортних одиниць .

Випадок 3. Показовий розподіл тривалості обслуговування транспортної одиниці, період 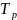детермінований.

При показовому розподіленні кількість транспортних одиниць, що обслуговуються на протязі періоду , описуються законом Пуассона, тобто:

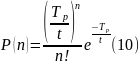
Вірогідність того, що пропускна здатність системи буде менше знаходиться із рівності:

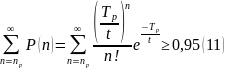
Випадок 4. Геометричний розподіл тривалості обслуговування транспортної одиниці, період обслуговування детермінований.

При геометричному розподілі тривалості обслуговування коливання описуються біноміальним законом:

Знайдемо вірогідність і параметр :

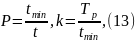
де 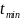– мінімальний термін обслуговування.

Пропускна здатність:

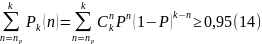
Для полегшення розрахунків значення сукупної вірогідності наведені в таблиці (1).

При великих значеннях 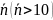біноміальний розподіл можна замінити нормальним з параметрами: математичне чекання , середнє квадратичне відхилення:

.

Випадок 5. Багатоканальна транспортна система, розподіл терміну обслуговування заявки каналів показове, період обслуговування детермінований.

Розподіл коливання пропускної здатності багатоканальної системи:

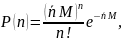
де 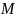– кількість каналів; – середня пропускна здатність каналу.

Вірогідність того, що пропускна здатність системи буде не менше , знаходимо із рівності:

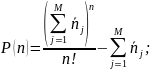
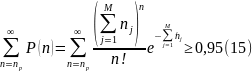
Випадок 6. Багатоканальна система, розподіл терміну обслуговування заявки геометричне: