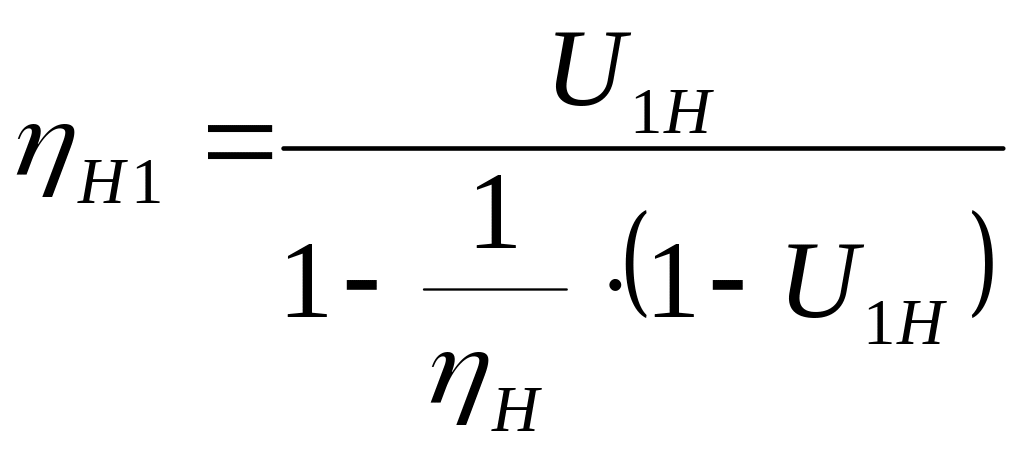- •2. Условные изображения кинематических пар и звеньев
- •3. Методика составления кинематических схем
- •Структурный анализ механизма
- •5. Контрольные вопросы
- •Лабораторная работа 1.
- •Класс порядок и вид каждой группы
- •Основной диаметр зубчатого колеса
- •Высота делительной ножки зуба
- •3. Контрольные вопросы
- •Лабораторная работа № 2 рсшифровка зубчатых колёс
- •1. Измерение зубчатых колес
- •В миллиметрах
- •3. Схемы измерений зубчатых колес
- •Лабораторная работа № 3 построение эвальвентных зубьев методом обкатки Задание
- •Порядок выполнения работы
- •2. Построение эвольвентного зацепления пары зубчатых колёс
- •3. Определение коэффициента перекрытия в зацеплении изготовленных колёс
- •4. Контрольные вопросы
- •Лабораторная работа № 3 построение эвольвентных зубьев методом огибания
- •4. Профили зубьев шестерни и колеса
- •1.1. Передаточное отношение одноступенчатых зубчатых передач
- •1.2. Передаточное отношение многоступенчатых зубчатых передач
- •Порядок выполнения работы
- •3. Контрольные вопросы
- •Лабораторная работа № 4 кинематический анализ зубчатых механизмов с неподвижными осями колёс
- •Лабораторная работа № 5
- •Общие сведения
- •1.1. Дифференциальные зубчатые механизмы
- •1.2. Планетарные механизмы
- •2 Порядок выполнения работы
- •3. Контрольные вопросы
- •Лабораторная работа № 5
- •Лабораторная работа № 6 статическое уравновешивание и балансировка роторов
- •1. Общие сведения
- •2. Статическая балансировка.
- •3. Постановка задачи.
- •4. Контрольные вопросы
- •Лабораторная работа № 6
- •1. Схема балансировочного станка и балансируемого звена
- •2. Результаты измерений
- •3. Векторное уравнение статической уравновешенности звеньев
- •4. Графическое решение векторного уравнения
- •Лабораторная работа № 7 динамическое уравновешивание вращающихся звеньев
- •1. Назначение работы.
- •2. Теоретические предпосылки
- •3. Описание установки
- •4. Порядок выполнения работы
- •5. Контрольные вопросы.
- •Лабораторная работа № 7
- •1. Схема установки
- •2. Исходные и вычисленные при уравновешивании ротора параметры
- •3. Векторные уравнения динамической уравновешенности ротора
- •4. Графическое решение векторных уравнений
- •Лабораторная работа № 8
- •1. Назначение работы.
- •2. Теоретические предпосылки
- •3. Описание станка дб-34 для динамической балансировки
- •4. Порядок выполнения балансировки ротора
- •5. Контрольные вопросы.
- •Лабораторная работа № 8
- •1. Схема балансировочного станка
- •2. Схема расположения плоскостей измерения и исправления неуравновешенности
- •3. Схема определения места неуровновешенности в двух плоскостях исправления
- •Определение величины дисбаланса
- •Лабораторная работа №9
- •1. Назначение работы
- •2. Измерение кинематических параметров
- •2.1. Измерение перемещений звеньев
- •2.2. Измерение скорости движения
- •2.3. Измерение ускорений звеньев
- •3. Обработка полученных при эксперименте данных
- •4. Порядок выполнения работы
- •5. Контрольные вопросы
- •Лабораторная работа № 9
- •Лабораторная работа №10
- •Описание экспериментальной установки.
- •2. Методика экспериментального определения кпд редуктора.
- •3. Определение кпд планетарного редуктора аналитически (расчетным методом).
- •4. Постановка задачи.
- •5. Контрольные вопросы
- •Лабораторная работа № 10
- •1. Схема установки
- •2. Схемы измерения сил давления статора на динамометр и
- •3. Основные параметры установки
Лабораторная работа №10
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОЛЕЗНОГО ДЕЙСТВИЯ РЕДУКТОРА
Описание экспериментальной установки.
Установка для экспериментального определения КПД редуктора (рисунок 1 и рисунок 2 ) состоит из электродвигателя 1 и редуктора 2, связанных упругой муфтой. Статор электродвигателя не закреплен и может свободно проворачиваться на валу ротора. Со статором жестко связан рычаг, который опирается на динамометр, как показано на рисунке 3. Динамометр состоит: из стальной пластины 1 и индикатора 2а. К ведомому валу редуктора (рисунок 2) присоединен тормозной механизм 4. Схема этого механизма показана на рисунке 4.

Рисунок 1.
Через тормозной шкив 4 перекинут ремень 5. Натяжение ветвей ремня определяется с одной стороны весом груза и с другой динамометром, состоящим из упругой пластины 1 и индикатора 2б.

Рисунок 2.

Рисунок 3.

Рисунок 4.
2. Методика экспериментального определения кпд редуктора.
Коэффициент полезного действия η для установившегося движения может быть определен как отношение средней мощности сил полезного сопротивления Nпс к средней мощности движущих сил Nд.
![]() (1)
(1)
В данном случае мощность движущих сил равна мощности на валу электродвигателя, а мощность сил полезного сопротивления равна мощности сил трения в тормозном механизме.
Мощность движущих сил можно определить следующим образом
Nд = Мд ·ωд (2)
где Mд - момент на валу двигателя, равный моменту, приложенному к статору;
ωд=ωн - угловая скорость электродвигателя равная угловой скорости оси ведущего звена редуктора.
Мощность сил полезного сопротивления:
Nnc = Мтр ·ω1 (3)
где Мтр - момент сил трения приложенных и ободу тормозного шкива;
ω1 - угловая скорость ведомого звена редуктора.
Подставляя в формулу 1 выражения 2 и 3 после преобразования получим :
![]() (4)
(4)
Из рассмотрения схем изображенных на рис. 2 и рис. 3 можно заключить, что:
Мд=Р·ℓ (5)
где Р - сила, с которой статор давит на динамометр;
ℓ - плечо силы.
Мтр =(S2-S1)·r (6)
где r - радиус тормозного шкива;
S1 - натяжение правой ветви ремня, равное весу груза;
S2 - натяжение девой ветви ремня, измеряемое динамометром.
Натяжение ветвей ремня, огибающих тормозной шкив, связаны формулой Эйлера:
S2=S1·еfα (7)
где е - основание натурального логарифма;
f - коэффициент трения;
α - угол обхвата шкива ремнем в рад.
3. Определение кпд планетарного редуктора аналитически (расчетным методом).
Величина КПД планетарного редуктора зависит от того, передается движение от центрального подвижного колеса к водилу или наоборот, а также от численного значения передаточного отношения.
В таблице 1 сведены формулы для определения КПД планетарного редуктора.
Таблица 1
|
1>U1H>0 |
U1H>1;U1H<0 |
От колеса к водилу |
|
|
От водила к колесу |
|
|
В этих формулах ηH - коэффициент полезного действия при обращенном движении планетарной передачи.
Указанные формулы относятся к определению потерь, возникающих вследствие трения между зубьями. Эти формулы приближенные, т.к. при выводе их мощность в зацеплении определялась без учета потерь на трение во вращательных парах.