
- •Міністерство освіти і науки україни
- •2 Практичні заняття
- •Рекомендована література
- •Завдання до контрольної роботи, а також приклади розв’язання подібних задач для студентів заочної форми навчання зі спеціальності „Інформатика”.
- •Приклад 2
- •Правила виконання та оформлення контрольних робіт
- •Вибір варіанта та номерів завдань
Міністерство освіти і науки україни
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
Методичні вказівки для організації самостійної роботи
по курсу "Функціональний аналіз"
для студентів заочного відділення спеціальності „ Інформатика”
ЗАТВЕРДЖЕНО
На засіданні кафедри
прикладної математики і механіки
Протокол № 1 від 30.08.04
Суми – 2004
Вступ
Курс функціонального аналізу, що викладається студентам спеціальності „Інформатика”, згідно робочої програми, розробленої на основі „Освітньо-професійної програми вищої освіти”, індекс 7.0802.02, переслідує наступні цілі:
Навчити студентів найбільш загальним математичним методам розв’язування задач обчислювальної, прикладної математики, фізики та інших природничих наук.
Дати студентам єдиний погляд на різноманітні розділи математики, такі як математичний аналіз, інтегральні та диференціальні рівняння, варіаційне числення, криптографія і т.п.
В результаті вивчення дисципліни студент повинен:
ЗНАТИ:
елементи теорії метричних просторів, простори
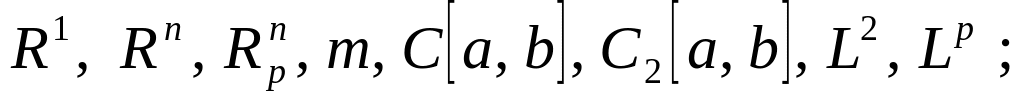
елементи теорії лінійних нормованих просторів;
основні означення теорії Евклідових та Гільбертових просторів;
елементи теорії лінійних функціоналів та операторів.
УМІТИ:
знаходити відстані між елементами в різних просторах;
застосувати принцип нерухомої точки до розв’язування рівнянь (скалярних, систем лінійних рівнянь, інтегральних рівнянь і т.п.);
будувати ортонормовані системи за допомогою процесу ортогоналізації Шмідта.
Курс „Функціональний аналіз” викладається студентам спеціальності „Інформатика” у 6-му семестрі.
Забезпечуючи навчальні дисципліни: математичний аналіз, алгебра і геометрія, теорія функцій дійсної змінної.
Матеріал дисципліни використовується в курсах теорії інформації, теорії алгоритмів.
Основними розділами (питаннями) даної дисципліни є:
Метричні простори.
Лінійні нормовані простори.
Гільбертові простори.
Лінійні функціонали в ЛНП.
Структура курсу складається з наступних блоків:
Метричні простори.
Лінійні нормовані простори.
Евклідові простори.
Гільбертові простори.
Лекційний матеріал викладається на настановчій сесії відповідно до таблиці 1.
1 Лекції
Номер розділу |
Ном. підрозділу чи теми |
Назви розділів, підрозділів, тем, та основні питання, що розглядаються |
Обсяг, год. |
Посилання на літературу |
1 |
2 |
3 |
4 |
5 |
1 |
|
Метричні
простори. Означення метричного
простору. Приклади метричних просторів,
простори
|
1,5 |
3.1.1: [1]-[3]. 3.1.3: [1] |
2 |
|
Повні метричні простори. Критерій Коші. Приклади. Лема про замкнені кулі. Принцип стискуючих відображень (ПСВ). Теорема Банаха. Застосування ПСВ для розв’язку скалярних рівнянь, СЛАР. |
2 |
3.1.1: [1]-[3]. 3.1.3: [1] |
1 |
2 |
3 |
4 |
5 |
3 |
|
Лінійні нормовані простори (ЛНП). Лінійні простори. Базис, підпростір, норма, зв’язок з метричним простором. Приклади ЛНП. Ізоморфізм. Банахові простори. Приклади. |
1,5 |
3.1.1: [1]-[4]. 3.2.1: [1] |
4 |
|
Евклідові та Гільбертові простори. Скалярний добуток, норма. Приклади Евклідових та Гільбертових просторів. Характеристична властивість Гільбертових просторів. Ортонормовані системи в Н. Процес ортогоналізації Шмідта. |
1,5 |
3.1.1: [1]-[4]. 3.1.3: [1] |
5 |
|
Апроксимація в Н. Відстань від елемента до підпростору. Теорема про проекцію в Н.Ортогональна декомпозиція. |
1,5 |
3.1.1: [1]-[3] |
|
|
Всього за семестр |
8 |
|
Практичні заняття відповідно до таблиці 2.
