Інтегрування ірраціональних функцій
Деякі типи інтегралів від алгебраїчних ірраціональностей потрібною заміною можна звести до інтегралів від раціональних функцій. Таке перетворення інтеграла прийнято називати його раціоналізацією.
1. Якщо під знаком інтеграла стоїть
раціональна функція від дробових
степенів незалежної змінної
,
тобто функція
,
тоді раціоналізація інтеграла проводиться
за допомогою підстановки
,
де
-
це найменше кратне чисел
.
2. Якщо під знаком інтеграла стоїть
раціональна функція від
і дробових степенів дробово-лінійної
функції виду
,
тобто функція
,
тоді раціоналізація інтеграла проводиться
за допомогою підстановки
,
де
-
це найменше кратне чисел
.
Приклад 1
Під знаком інтеграла стоїть раціональна
функція від дробових степенів незалежної
змінної
,
тобто функція
.
Найменше спільне кратне чисел 3, 6 дорівнює
6, тому зробимо наступну підстановку:
,
.
Звідси отримаємо
.
Проводячи зворотну заміну,
,
отримаємо
.
Приклад 2
Під знаком інтеграла стоїть раціональна
функція від дробових степенів незалежної
змінної
,
тобто функція
.
Найменше спільне кратне чисел 2,
3, 4 дорівнює 12, тому зробимо наступну
підстановку:
,
.
Звідси отримаємо
Провівши ділення по схемі Горнера, отримаємо
Проводячи зворотну заміну
остаточно отримаємо
.
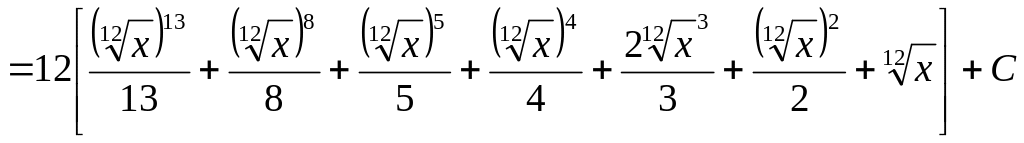Приклад 3
Підінтегральний вираз є раціональною
функцією від
,
тому покладемо
,
звідки
;
;
.
Отже,
.
Повертаючись до змінної , отримаємо
.
Приклад 4
.
Підінтегральний вираз є раціональною
функцією від змінної
та від виразу
,
тому зробимо наступну підстановку:
;
,
звідки
;
;
.
Отже,
.
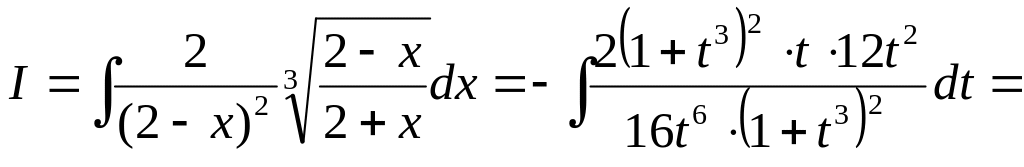
Для самостійної роботи пропонуємо обчислити наступні інтеграли:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Інтегрування диференціального біному
Інтеграл виду
,
де
-
раціональні числа, виражається через
елементарні функції тільки в наступних
трьох випадках.
1.
-
ціле.
Тоді, якщо
,
підінтегральний вираз розгортається
по формулі бінома Ньютона; якщо ж
,
тоді проведемо заміну
,
де
-
спільне кратне знаменників
і
.
2.
-
ціле.
Покладемо
,
де
-
знаменник дробу
.
3.
-
ціле.
Покладемо
,
де
-
знаменник дробу
.
Приклад 1
Так як
,
,
,
маємо 1-й випадок. Проведемо наступну заміну
, .
Отримаємо
Розкладаючи підінтегральний дріб на прості дроби, отримаємо
Перший інтеграл є табличним, а в другому
проведемо заміну
,
і враховуючи, що
,
отримаємо:
.
Приклад 2
Визначимо можливу заміну:
,
,
,
тобто
- ціле число.
В цьому випадку застосуємо підстановку
,
,
.
Отримаємо
Розклавши підінтегральний дріб на прості дроби, отримаємо
.
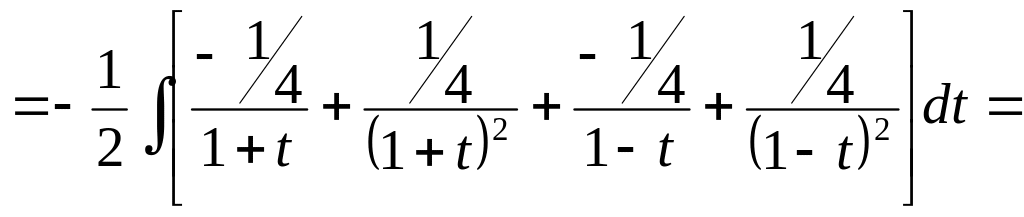
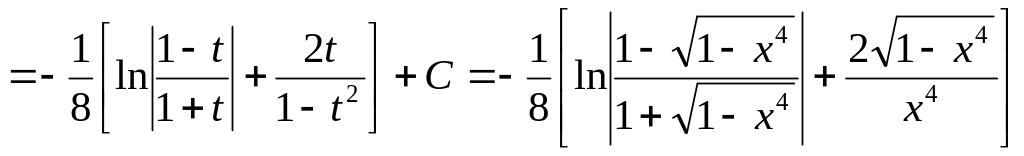Приклад 3
Враховуючи, що
,
,
,
отримаємо
,
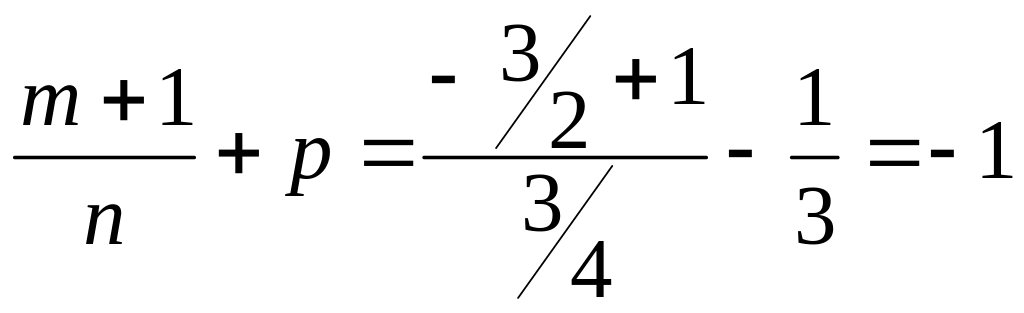тобто визначимо наступну заміну
,
,
.
Підставимо в інтеграл:
Провівши певні скорочення, отримаємо
.
Провівши відповідні заміни, знайти наступні інтеграли.
а)
б)
в)
;
г)
д)
е)
Обчислити наступні інтеграли.
1. 
2. 
3. 
4.
5. 
6.
