Квадратний тричлен
Інтеграли виду
і
зводяться до табличних за допомогою
підстановки
або виділенням повного квадрату в
квадратному тричлені:
,
.
Приклад 1
Розв’язується заміною
.
Приклад:
= (розбиваємо на 2 інтеграли)
.
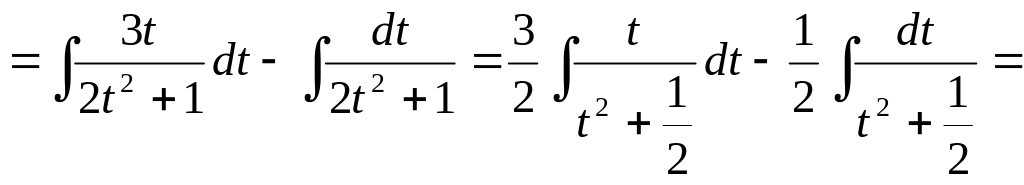
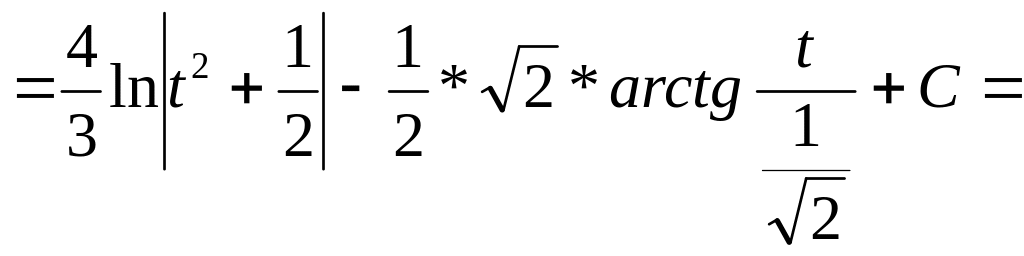
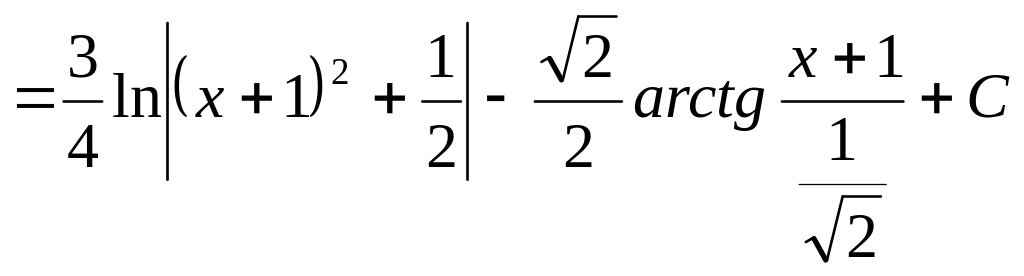Приклад 2
Проведемо деякі перетворення
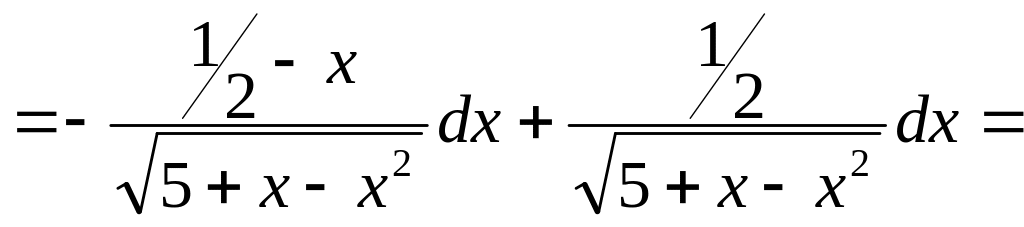
Тобто наш інтеграл прийме вид
Як видно, перший інтеграл є табличним, а в другому, в знаменнику, в підкореневому виразі, виділимо повний квадрат.
Тобто, отримаємо
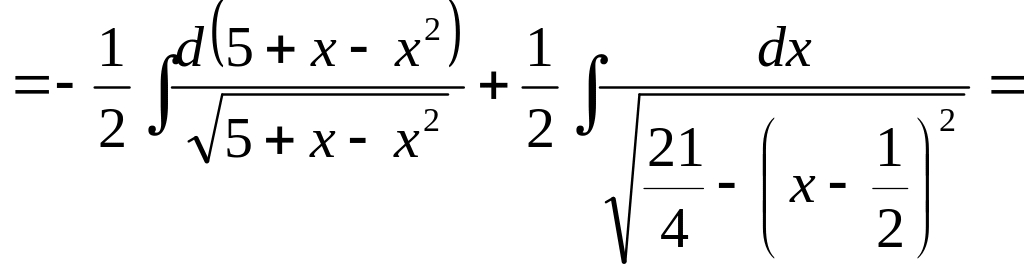
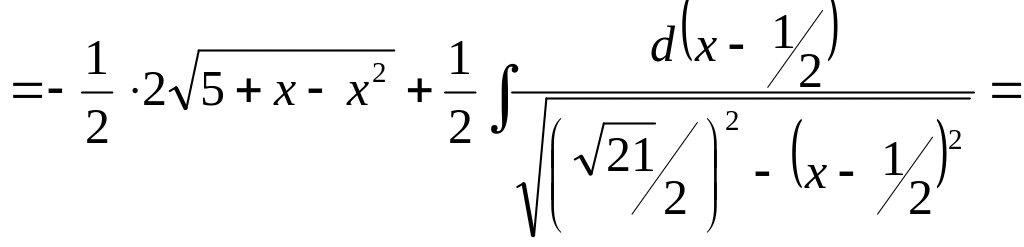
І остаточно
.
Приклад 3
Перед виділенням повного квадрату в знаменнику, проведемо деякі перетворення підінтегрального виразу
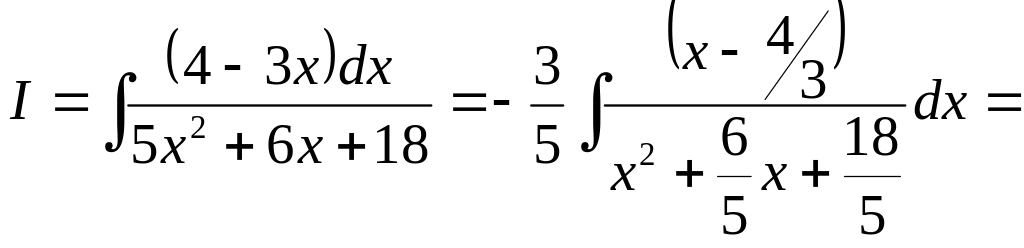
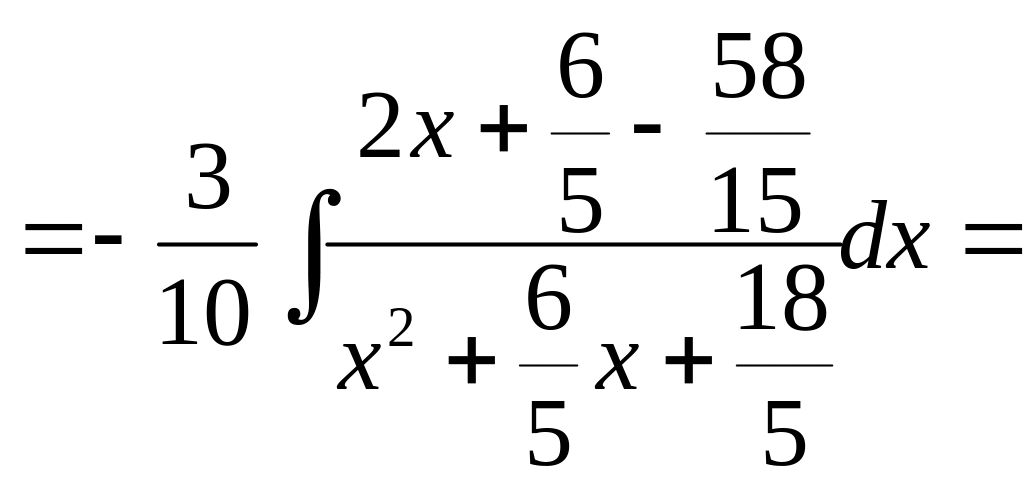
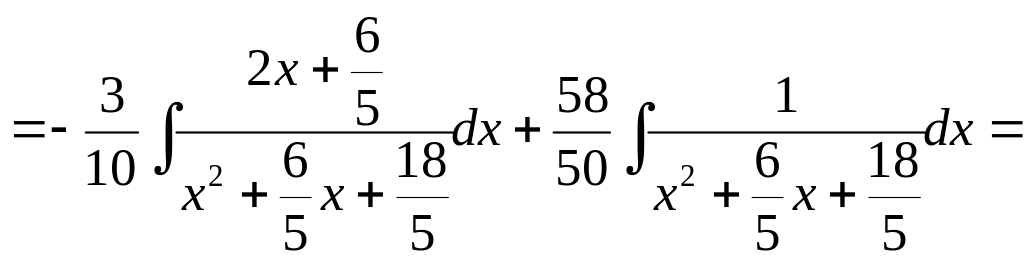
Виділимо повний квадрат в знаменнику другого інтеграла
Тоді наш інтеграл прийме наступний вид
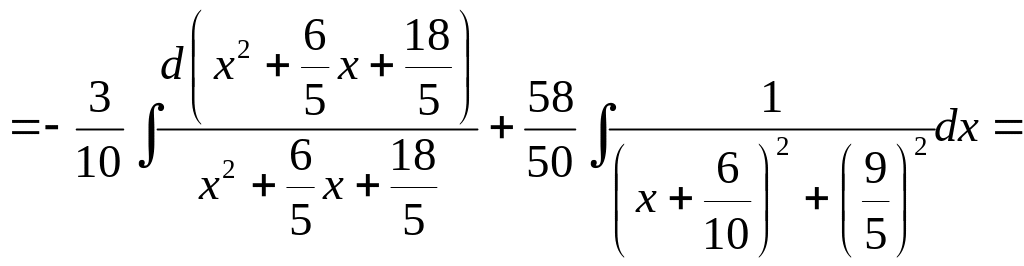
Згідно правил інтегрування
І остаточно
.
Приклад 4
Для обчислення даного інтеграла використаємо наступну формулу
,
де
,
- многочлен степені
,
- многочлен степені
і
- число.
Застосовуючи дану формулу, отримаємо
.
Для знаходження невідомих коефіцієнтів продиференціюємо дану рівність і приведемо до спільного знаменника:
.
Утворимо систему для відшукання коефіцієнтів
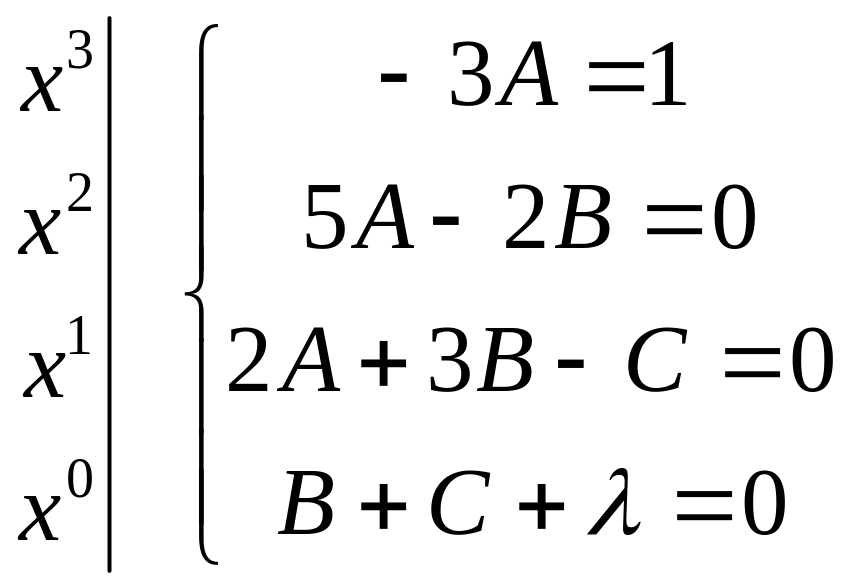
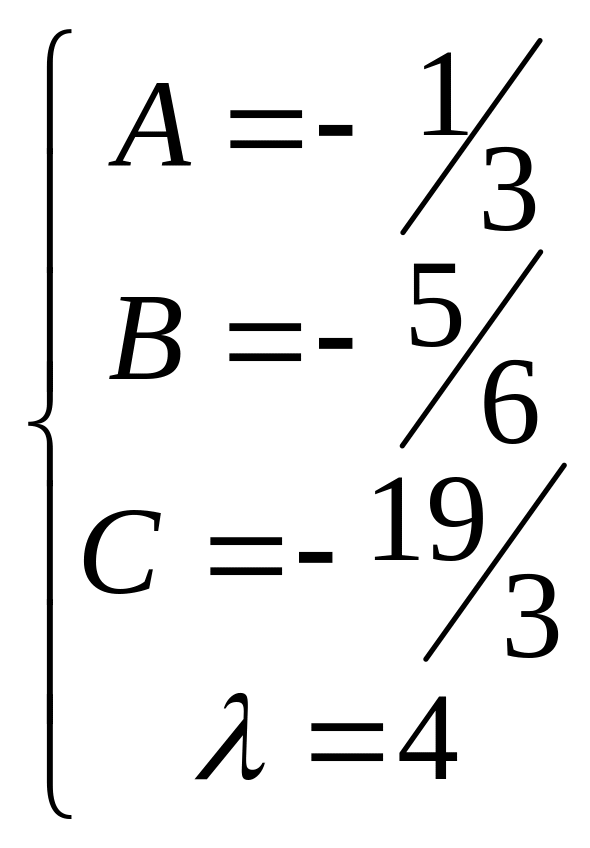
Виділивши повний квадрат в підкореневому виразі другого інтеграла
отримаємо, при
.
Приклад 5
Зробимо підстановку
;
;
.
Отримаємо
.
Застосовуючи формулу з попереднього прикладу, отримаємо
.
Диференціюючи
по
і приводячи до спільного знаменника,
отримаємо наступну тотожність
,
звідки
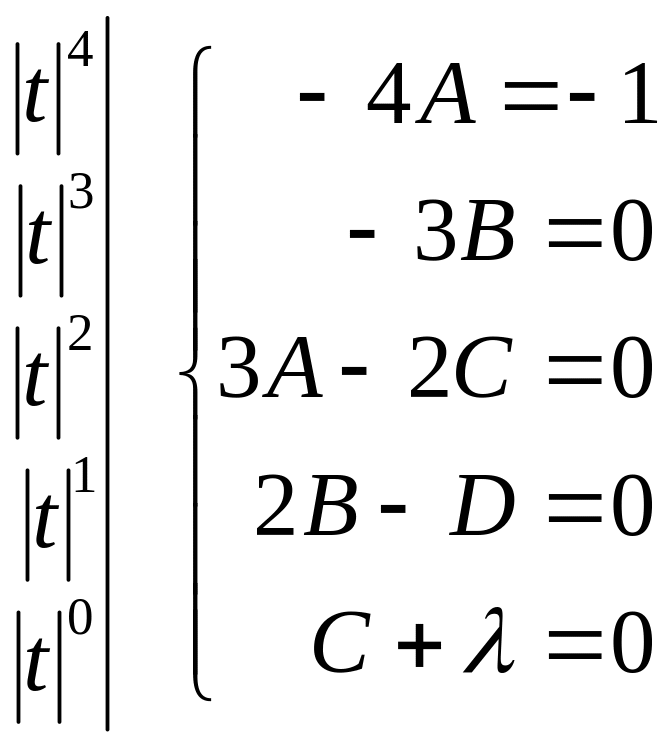
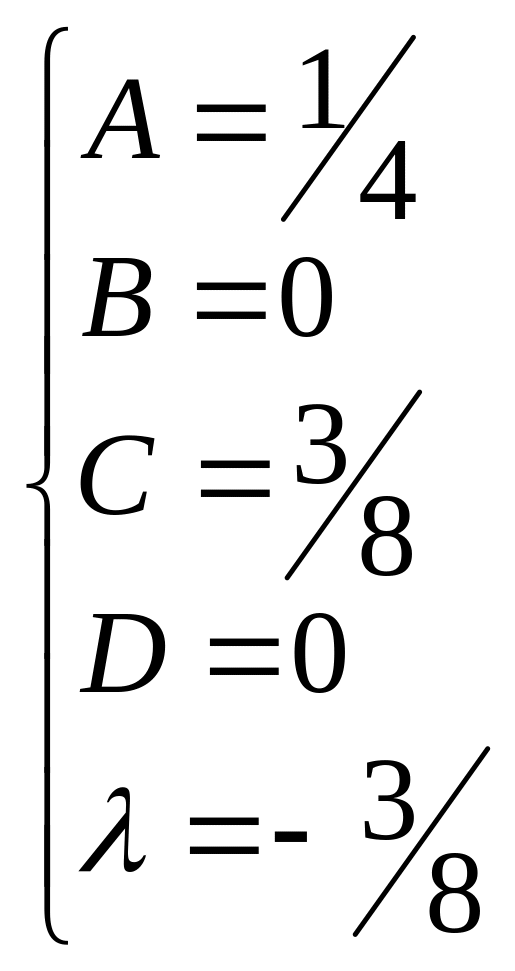
Таким чином
І остаточно
,
причому
.
Обчислити інтеграли:
а)
б)
в)
г)
д)
е)
є)
ж)
Виділити повний квадрат і звести до квадрату двочлена:
а)
б)
в)
г)
2. Обчислит
інтеграли:
а) 
б)
в)
г)
д)
е)
є)
Знайти інтеграли, використавши метод розкладу підінтегрального виразу і прийом виділення повного квадрату.
1.
2.
3.
4.
5.
6.
7.
8.
а)
б)
в)
г)
д)
е)
