Розділ 3 застосування визначеного інтеграла

21.Обчислення площі плоских фігур

Якщо на відрізку функція неперервна і , то площу криволінійної трапеції, обмеженої кривою і прямими , , , знаходять за формулою

.

+ +

0 a - b x

Відомо, що визначений інтеграл на відрізку представляє собою площу криволінійної трапеції, обмеженої графіком функції f(x). Якщо графік розміщений нижче осі Ох, тобто f(x) < 0, тоді площа має знак “-“, якщо графік розміщений вище осі Ох, тобто f(x) > 0, тоді площа має знак “+”.

Для знаходження сумарної площі використовується формула

.

Якщо функція на відрізку скінчене число разів змінює знак, то

.

Площу фігури, обмеженої кривими і і прямими та за умови, що , знаходять за формулою

.

Коли криволінійна трапеція обмежена кривою, заданою параметрично

, ,

прямими , і віссю , то її площа обчислюється за формулою

,

де , і на відрізку .

Площа криволінійного сектора, обмеженого кривою, заданою в полярній системі координат неперервною функцією і променями та ,

 = f()



О 

обчислюється за формулою

.

Приклад 1

Знайти площу фігури, обмеженої лініями y = x, y = x², x = 2.

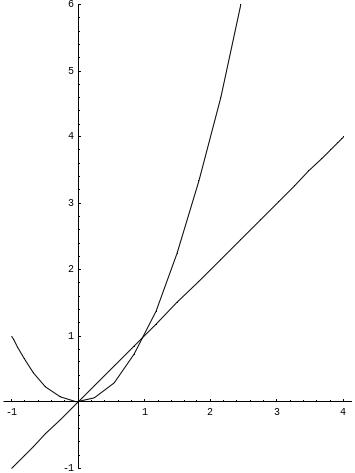
Шукана площа (заштрихована на малюнку) може бути знайдена по формулі:

(од²)

Приклад 2

Обчислити площу фігури, обмеженої лініями:

, .

Приклад 3

Знайти площу фігури, обмеженої параболами

, .

Приклад 4

Обчислити площу фігури, обмеженої однією аркою циклоїди

,

і віссю абсцис.

Приклад 5

Знайти площу фігури, обмеженої колом і кардіоїдою (ззовні кардіоїди).

Користуючись вищенаведеним, обчислити площі фігур.

1. Обчислити площу фігур, обмежену лініями, рівняння яких i

2. Обчислити площу фігури обмежену параболами і .

3. Обчислити площу фігури обмежену параболами і .

4. Найти площу фігур, на які парабола ділить окружність

5. Окружність розбивається гіперболою на три частини. Знайти площу цих частин.

6. Обчислити площу фігури, що знаходиться всередині між лінією і параболою .

7. Знайти площу фігури обмежену віссю координат і лінією .

8. Знайти площу петлі лінії

9. Знайти площу фігури, обмежену замкнутою лінією

10. Знайти площу кінцевої частини фігури, обмеженої лініями i

11. Обчислити площу фігури, обмеженої лініями і

12. Обчислити площу криволінійного трикутника, обмеженого віссю ординат і лініями , .

13. Обчислити площу фігури, обмеженою астроїдою , .

14. Знайти площу петлі лінії

1. , ;

2. ,

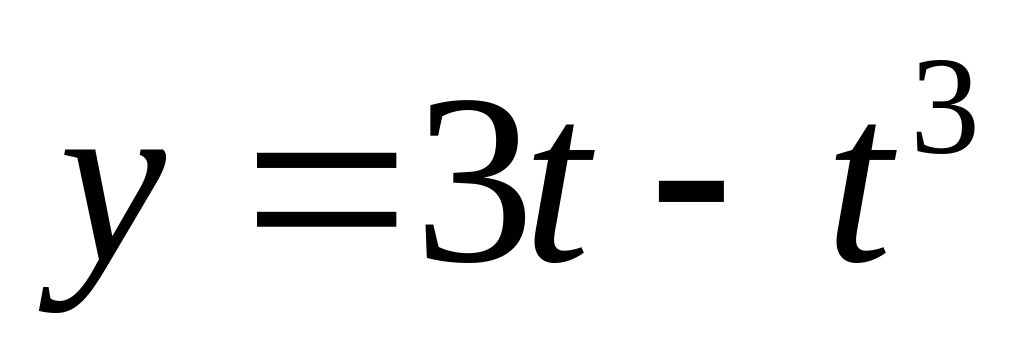15. Знайти площу фігури обмеженої лінією

16. Знайти площу частини фігури, обмеженої лінією , яка лежить за межами лінії .

В наступних задачах зручно перейти попередньо до полярних координат.

17. Знайти площу фігури, обмеженою лемніскатою Бернуллі

18. Знайти площу фігури, обмеженої лінією

19. Знайти площу фігури, яка знаходиться між лінією і її асимптотою.

20. Для лінії знайти площу петлі і площу фігури, яка знаходиться між лінією і її асимптотою.