
- •Лекція 1
- •1.1. Первісна
- •1.2. Невизначений інтеграл
- •1.3. Властивості невизначеного інтеграла
- •1.5. Основні методи інтегрування
- •Лекція 2 Інтегрування дробово - раціональних і деяких ірраціональних функцій
- •2.1. Інтегрування елементарних дробів
- •2.2. Інтегрування раціональних дробів
- •2.3. Інтегрування ірраціональних функцій
- •Приклад.
- •Приклад.
- •Лекція 3 Інтегрування тригонометричних функцій. Застосування невизначених інтегралів.
- •3.1 Інтегрування деяких тригонометричних функцій
- •Вправи. Обчислити інтеграли.
- •3.2 Застосування невизначенх інтегралів
- •Вправи.
- •Лекція 4 Визначений інтеграл
- •3.1. Приклади задач, які приводять до поняття визна-
- •3.3 Властивості визначеного інтеграла.
- •4.4. Обчислення визначеного інтеграла за допомогою
- •5.1. Інтегрування заміною змінної (метод підстановки)
- •5.2. Інтегрування частинами
- •5. Невластиві інтеграли
- •5.3 Невластиві інтеграли першого роду
- •Ознаки збіжності невластивих інтегралів першого роду.
- •5.4. Невластиві інтеграли другого роду.
- •6.1. Геометричні застосування інтеграла.
- •6.3. Обчислення об’ємів тіл.
- •Обчислення площ поверхонь обертання.
- •Теоретичні (екзаменаційні) питання.
5.1. Інтегрування заміною змінної (метод підстановки)
Теорема.
Якщо функція
f(x)
неперервна на відрізку [a,b]
, а функція x=(t)
і її похідна![]() неперервні на відрізку
[,]
, причому
неперервні на відрізку
[,]
, причому
![]() для всіх
для всіх
![]() ,
то
,
то
![]() (5.1)
(5.1)
Доведення.
Нехай Ф(x)
- яка - небудь первісна функції f(x)
на відрізку
![]() ;
тоді - функція
;
тоді - функція
![]() є первісною для функції
є первісною для функції
![]() на відрізку
на відрізку
![]() тому за форму-лою Ньютона-Лейцбніца
тому за форму-лою Ньютона-Лейцбніца
![]()
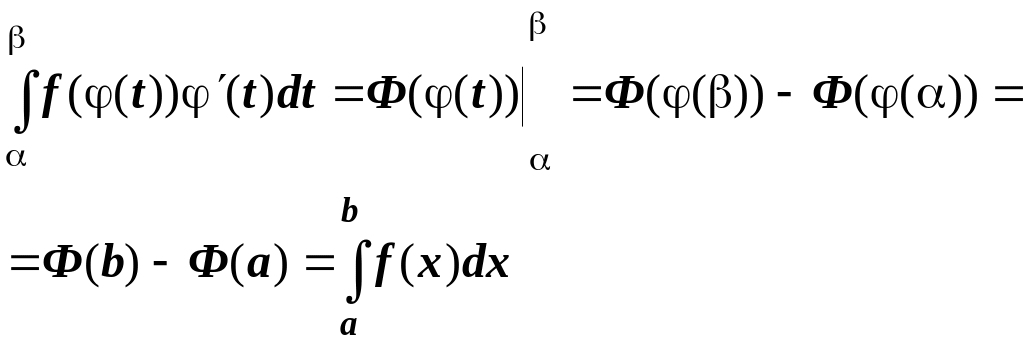 (5.2)
(5.2)
Формула (5.1) називається формулою заміни змінної у визначеному інтегралі , або формулою інтегрування підстановкою. На відміну від невизначеного інтегралу тут не потрібно повертатися до старої змінної, але треба поміняти межі інтегрування.
Приклади. Обчислити інтеграли:
![]()
![]()
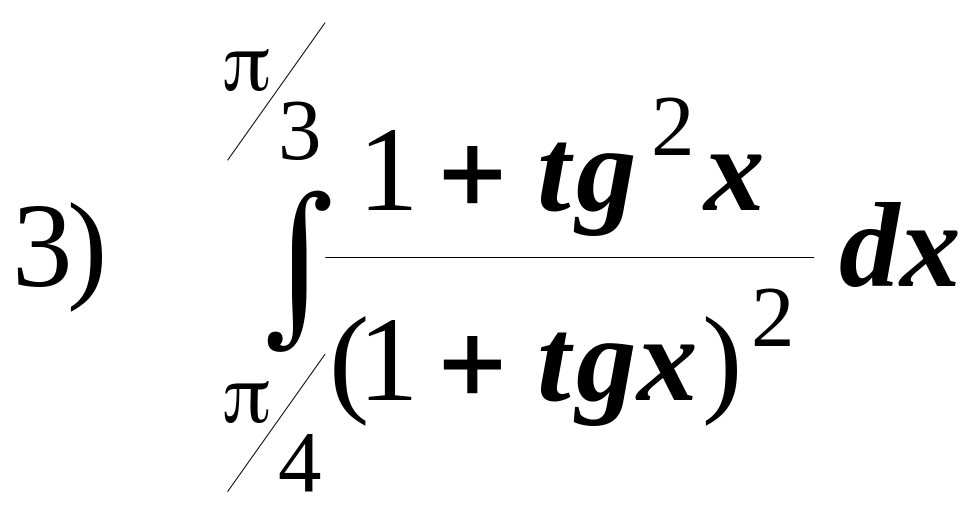
Розв’язання.:
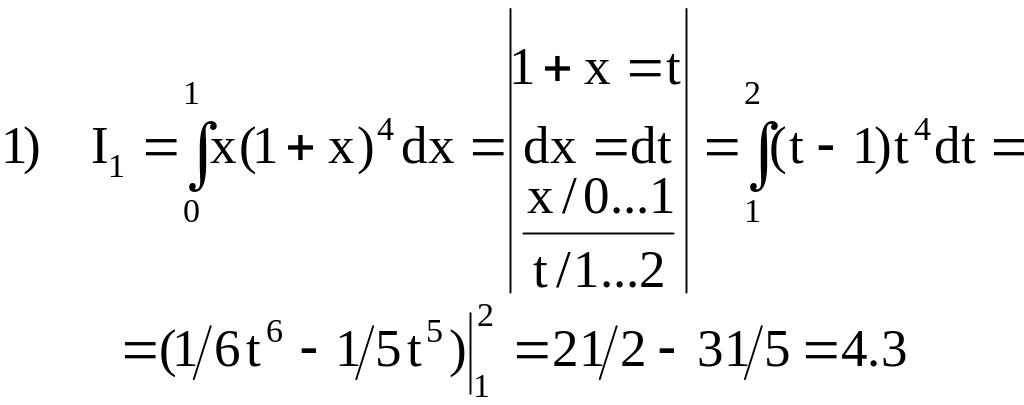
![]()
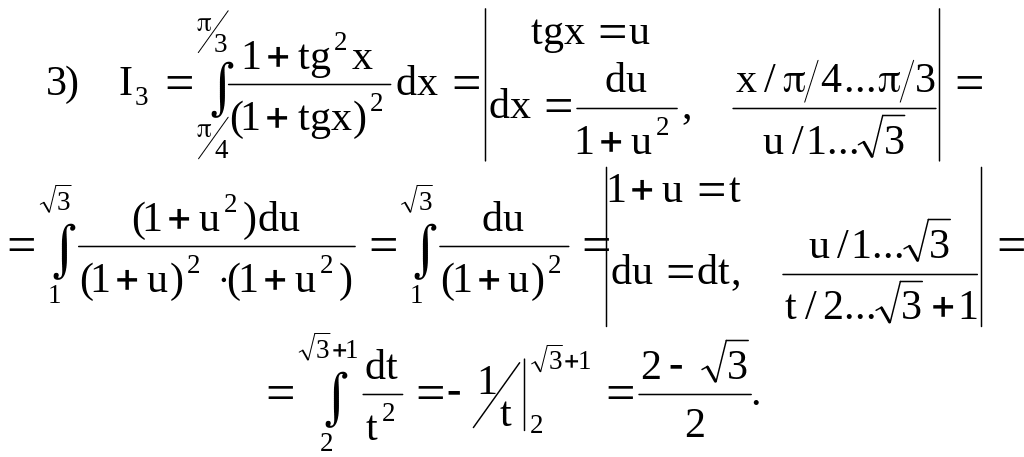
5.2. Інтегрування частинами
Теорема.
Якщо функції
u(x)
і v(x)
неперервні разом зі своїми похідними
u/(x)
та
v/(x)
на відрізку [a,b],
то
![]() (5.3)
(5.3)
Для
скорочення записів аргумент в дужках
писати не будемо; врахуємо, що v/dx=dv,
u/
dx=du,
і
![]()
Відомо d(uv)=vdu+udv , звідси udv= d(uv)- vdu.
Зінтегруємо останню рівністьв межах від а до b.
![]()
Оскільки
![]() ,
то маємо
,
то маємо
![]() .
.
Функції uv/ і vu/ неперервні (за умовою) на відрізку , тому інтеграли, що є в (5.3) , існують.
Приклади. Обчислити інтеграли:
1)
![]() 2)
2)
![]() 3)
3)
![]()
Poçâ’язання.
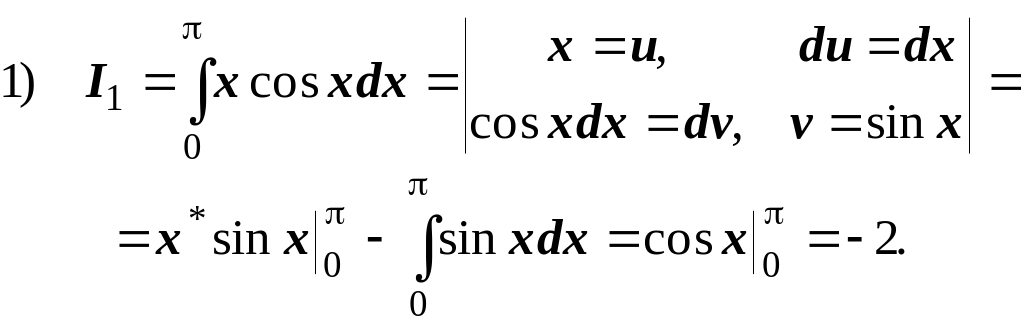
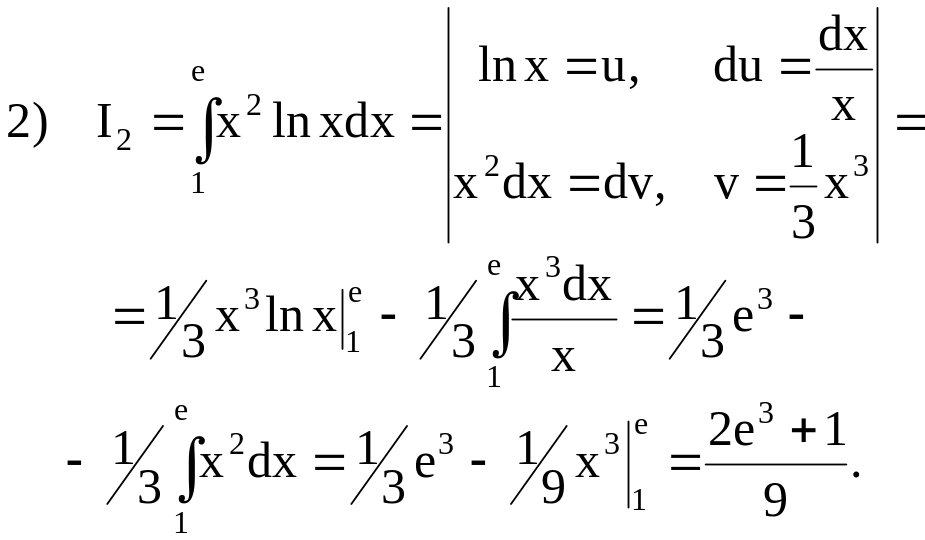
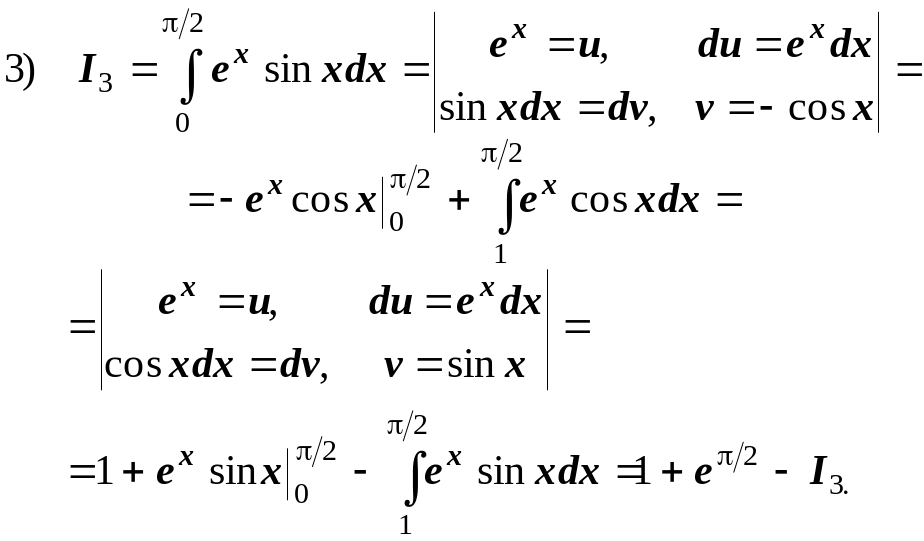
Маємо
![]() або
або
![]() .
.
Звідси
![]() .
.
Вправи. Обчислити інтеграли
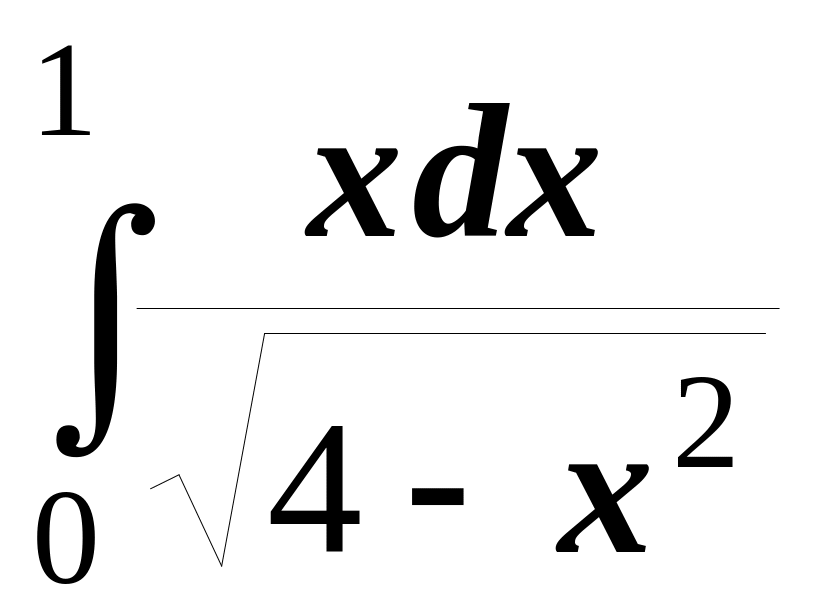 2.
2.
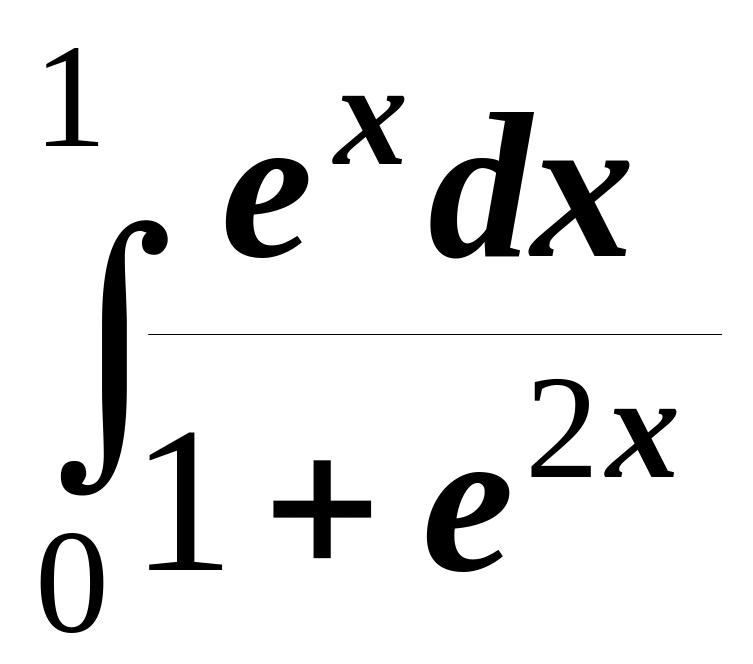 3.
3.
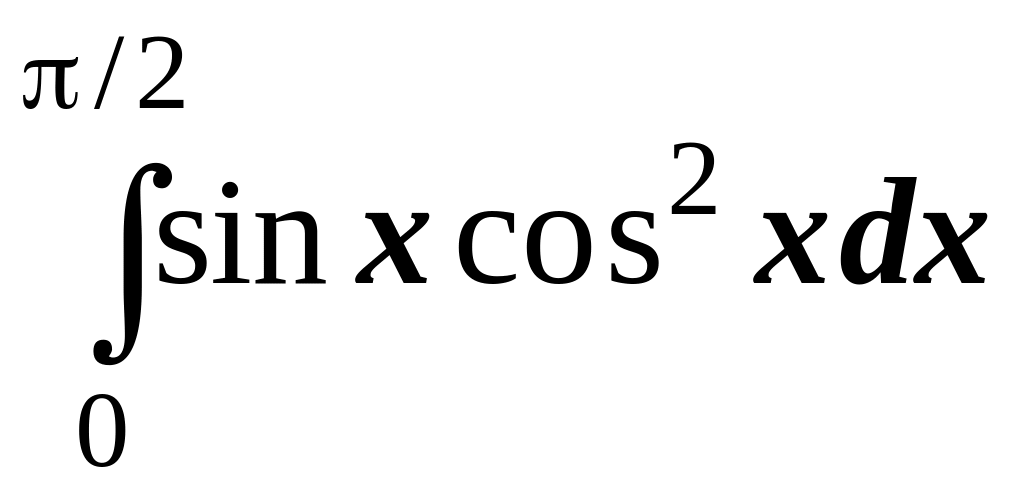
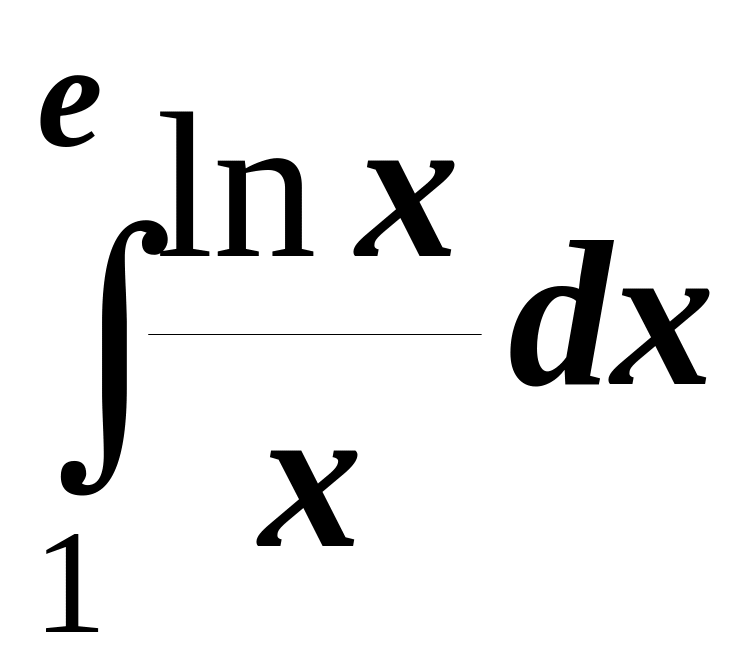 5.
5.
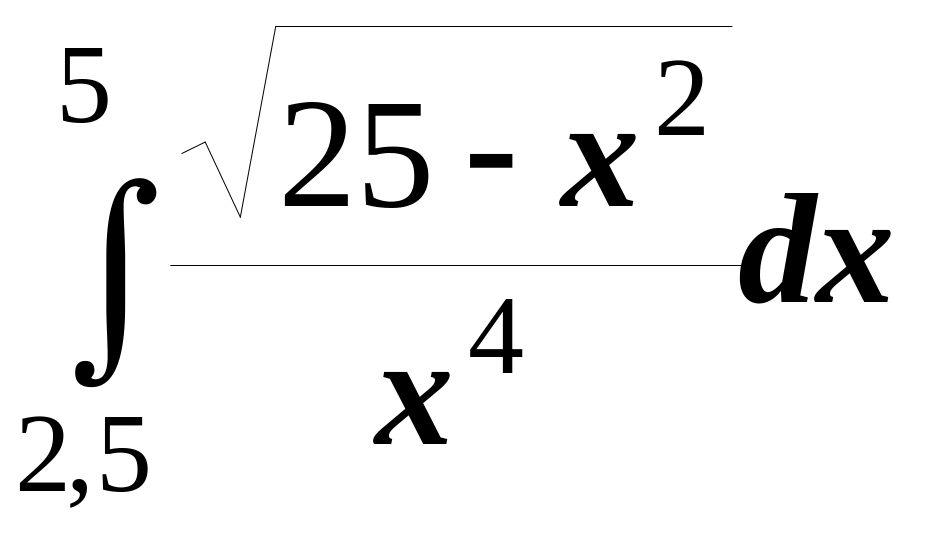 6.
6.
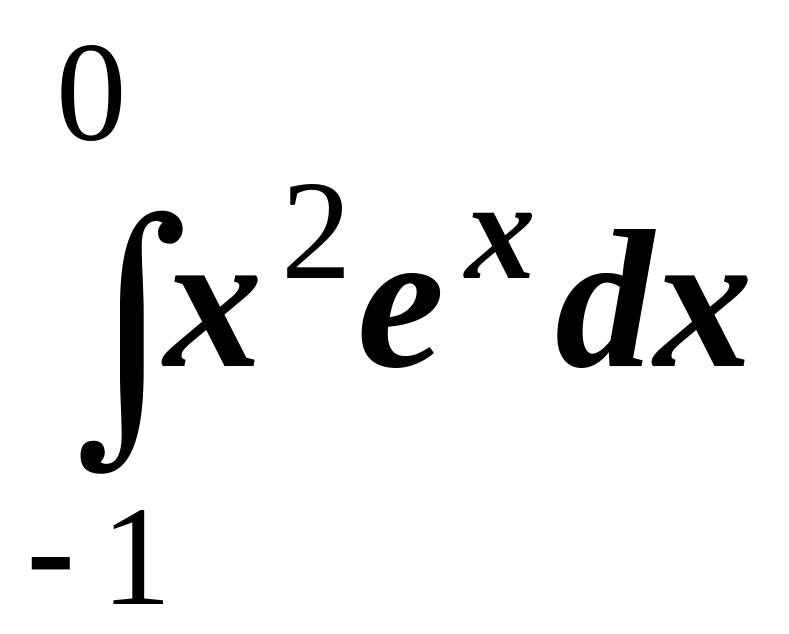
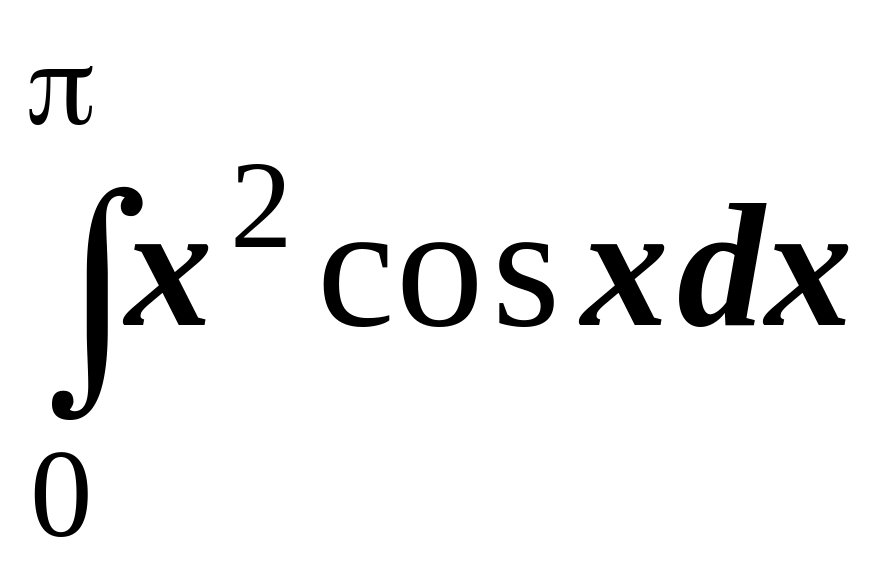 8.
8.
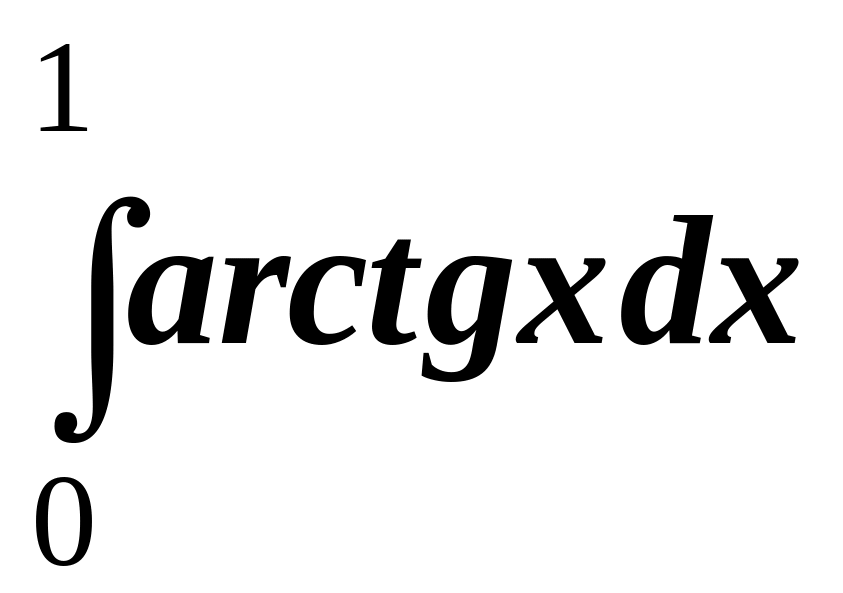 9.
9.
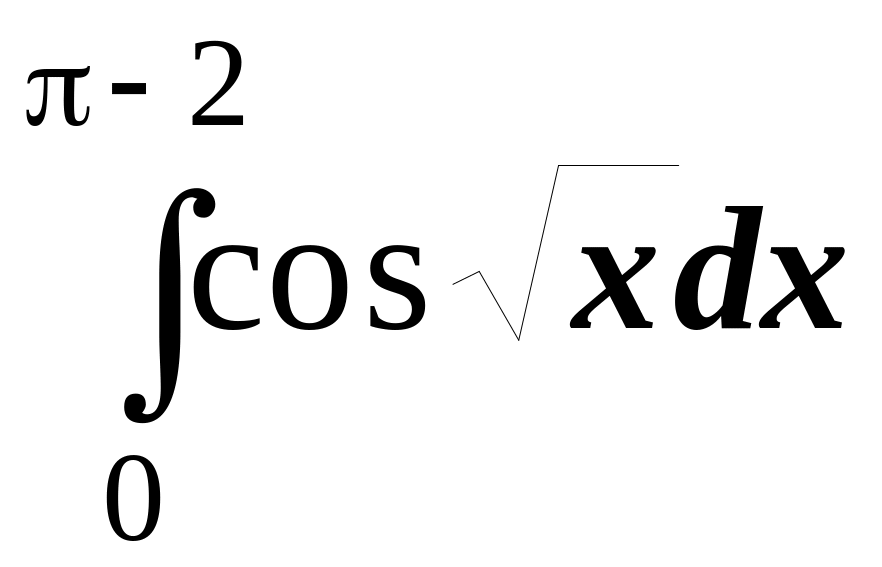
10.
![]()
Відповіді.
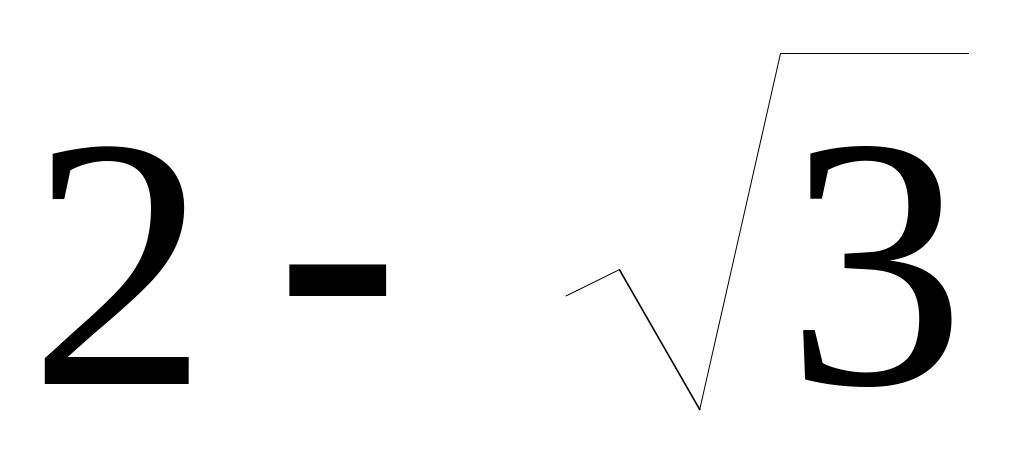 .
2.
.
2.
 . 3.
. 3.
 .
4.
.
4.
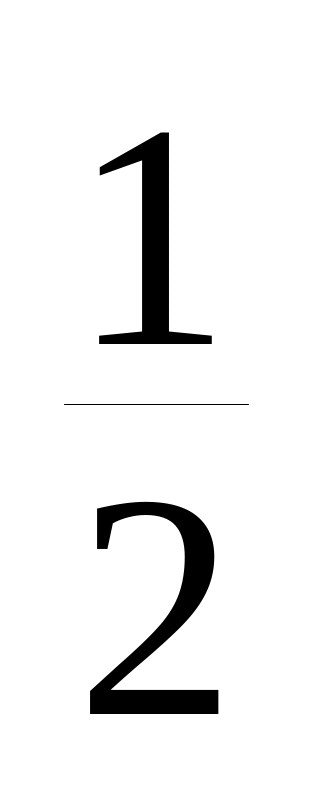 .
5.
.
5.
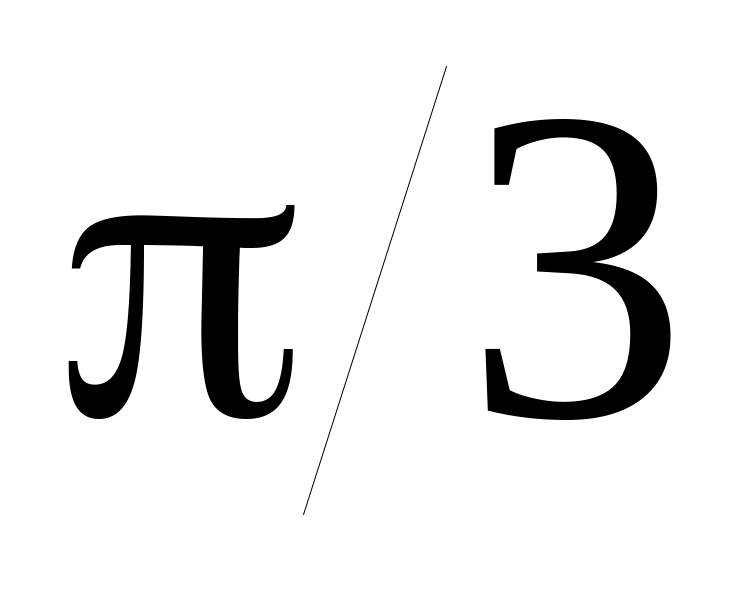 6.
6.
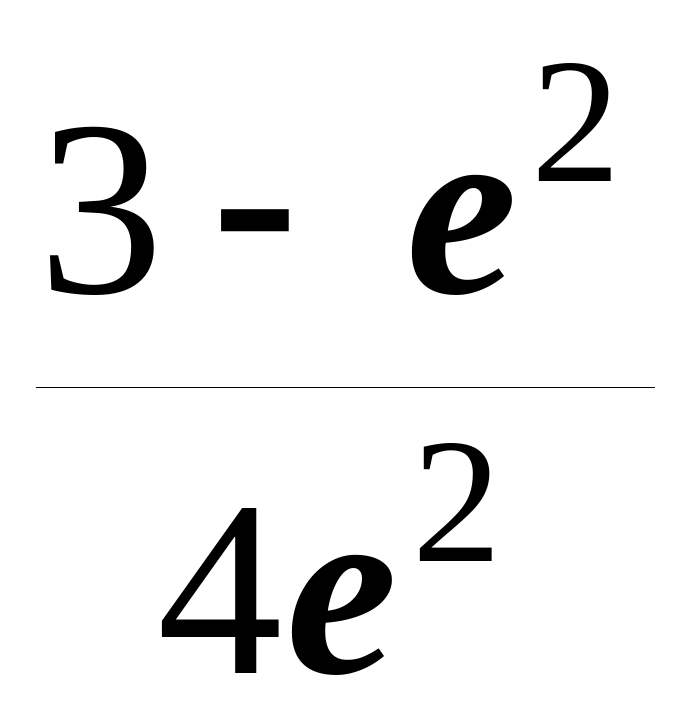 .
.
7.
![]() .
8.
.
8.
![]() . 9. -4. 10.
. 9. -4. 10.
![]() .
.
5. Невластиві інтеграли
В
означенні визначеного інтеграла
![]() допускалось , що функція
допускалось , що функція
![]() визначена і обмежена на скінченному
проміжку [a.b].Якщо
не виконується принаймі одна з цих умов,
то визначений інтеграл побудувати не
можна. Тоді будують нові інтеграли. Їх
називають невластивими визначеними
інтегралами: невластиві інтеграли
першого роду (або інтеграли з нескінченними
проміжками інтегрування), якщо інтервал
нескінченний, і невластиві інтеграли
другого роду (інтеграли необ-межених
функцій), якщо функція необмежена.
Корис-туючись геометричним тлумаченням
інтеграла, можна відповідно говорити
про площу трапеції з нескінченною
основою чи з нескінченною висотою Цікаво
, що в деяких випадках такі трапеції
мають скінченну площу в певному розумінні
визначена і обмежена на скінченному
проміжку [a.b].Якщо
не виконується принаймі одна з цих умов,
то визначений інтеграл побудувати не
можна. Тоді будують нові інтеграли. Їх
називають невластивими визначеними
інтегралами: невластиві інтеграли
першого роду (або інтеграли з нескінченними
проміжками інтегрування), якщо інтервал
нескінченний, і невластиві інтеграли
другого роду (інтеграли необ-межених
функцій), якщо функція необмежена.
Корис-туючись геометричним тлумаченням
інтеграла, можна відповідно говорити
про площу трапеції з нескінченною
основою чи з нескінченною висотою Цікаво
, що в деяких випадках такі трапеції
мають скінченну площу в певному розумінні
5.3 Невластиві інтеграли першого роду
Вважатимемо, що відповідна функція інтегрована на будь-якому скінченному інтервалі, що міститься в нескінченному.
Означення.
Скінченна границя
![]() (якщо вона
(якщо вона
існує)
називається невластивим інтегралом
функції f
пер-шого роду і позначається
![]() ,
тобто
,
тобто
![]() (5.4)
(5.4)
Аналогічно визначаються невластиві інтеграли для інших нескінченних інтервалів:
![]() (5.5)
(5.5)
![]() ,
(5.6)
,
(5.6)
де с - будь - яке число.
Якщо існує скінченна границя (5.4), то кажуть що невластивий інтеграл збігається . Якщо границя (5.4) не існує або нескінченна , то інтеграл (5,4) розбігається.
Розглянемо приклади , які приводять до таких інтег-ралів.
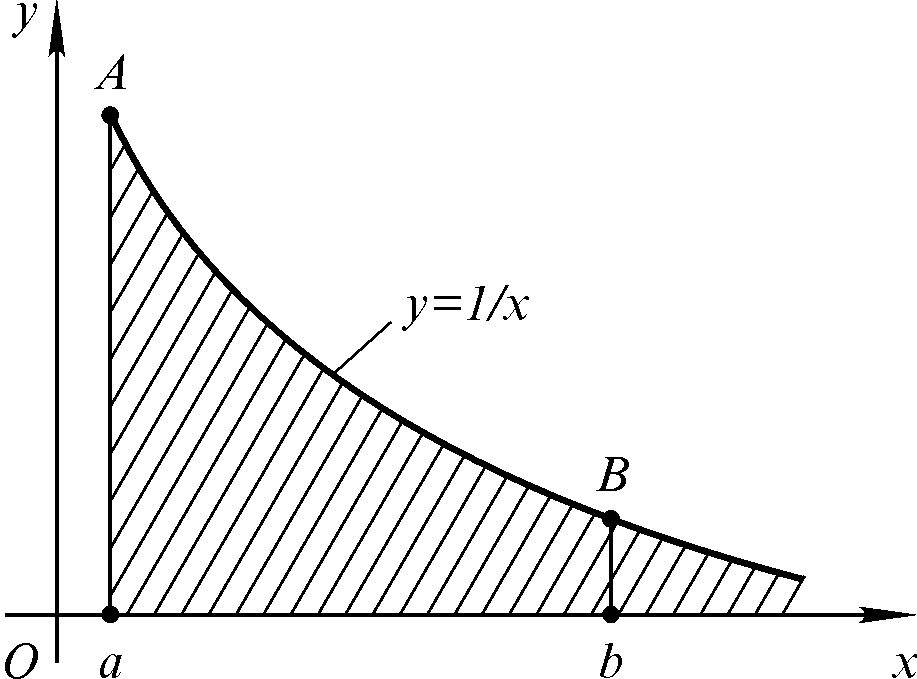
Рисунок 5.1
Знайдемо
площу S
під кривою
![]() (Рис5.1). Площу заштрихованої фігури
безпосередньо обчислити важко. Однак
, якщо відрізати нескінченний “
хвіст” прямою x=b
, то площу криволінійної трапеції aABb
можна обчислити за допомогою визначеного
інтег-рала
(Рис5.1). Площу заштрихованої фігури
безпосередньо обчислити важко. Однак
, якщо відрізати нескінченний “
хвіст” прямою x=b
, то площу криволінійної трапеції aABb
можна обчислити за допомогою визначеного
інтег-рала
![]() Якщо
Якщо
![]() ,
то ми повинні отримати площу всієї
заштрихованої фігури, тобто
,
то ми повинні отримати площу всієї
заштрихованої фігури, тобто
![]()
2.
Обчислимо площу S
під кривою![]() ,
,![]() (рис.5.2).
(рис.5.2).
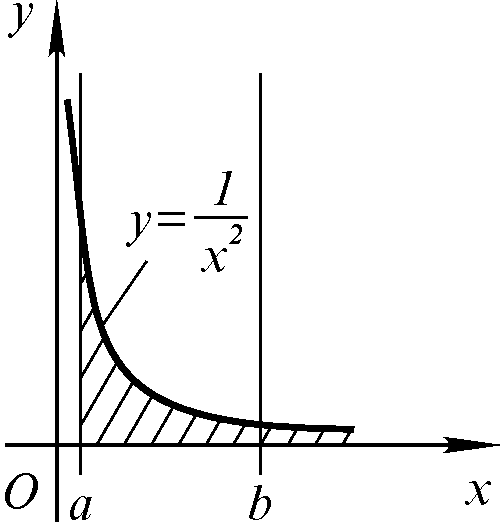
Рисунок 5.2
Як і в попередньому прикладі, маємо
![]() .
.
Отже, в даному випадку площа нескінченного “хвоста” скінченна і дорівнює 1/а.
3.
Обчислити інтеграл
![]()
Розв’язання.
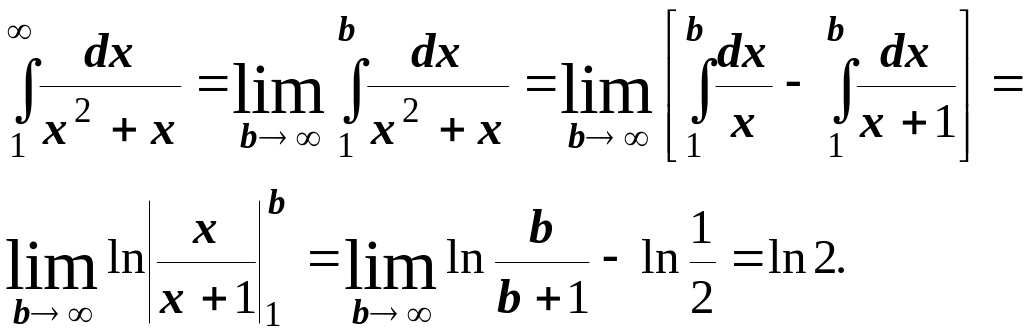
Отже, інтеграл збігається.
4.
Обчислити
![]() .
.
Розв’язання.
![]() .
.
![]() ;
;
![]() Тоді
Тоді
![]() ,
тобто інтеграл збігаєть-ся.
,
тобто інтеграл збігаєть-ся.
