
- •Лекція 1
- •1.1. Первісна
- •1.2. Невизначений інтеграл
- •1.3. Властивості невизначеного інтеграла
- •1.5. Основні методи інтегрування
- •Лекція 2 Інтегрування дробово - раціональних і деяких ірраціональних функцій
- •2.1. Інтегрування елементарних дробів
- •2.2. Інтегрування раціональних дробів
- •2.3. Інтегрування ірраціональних функцій
- •Приклад.
- •Приклад.
- •Лекція 3 Інтегрування тригонометричних функцій. Застосування невизначених інтегралів.
- •3.1 Інтегрування деяких тригонометричних функцій
- •Вправи. Обчислити інтеграли.
- •3.2 Застосування невизначенх інтегралів
- •Вправи.
- •Лекція 4 Визначений інтеграл
- •3.1. Приклади задач, які приводять до поняття визна-
- •3.3 Властивості визначеного інтеграла.
- •4.4. Обчислення визначеного інтеграла за допомогою
- •5.1. Інтегрування заміною змінної (метод підстановки)
- •5.2. Інтегрування частинами
- •5. Невластиві інтеграли
- •5.3 Невластиві інтеграли першого роду
- •Ознаки збіжності невластивих інтегралів першого роду.
- •5.4. Невластиві інтеграли другого роду.
- •6.1. Геометричні застосування інтеграла.
- •6.3. Обчислення об’ємів тіл.
- •Обчислення площ поверхонь обертання.
- •Теоретичні (екзаменаційні) питання.
3.3 Властивості визначеного інтеграла.
За означення приймемо
а)
![]()
б)
![]()
Це зрозуміло, якщо згадати геометричний зміст інтеграла. Деякі з властивостей випливають з означення визначеного інтеграла, а доведення інших зрозумілі інтуїтивно.
1. Однорідність.
![]()
2. Аддитивність за функцією.
![]()
Наслідок.
![]()
3. Аддитивність за проміжком.
![]()
при довільному розміщенні точок a, b, c (якщо с[ a, b ], то властивість очевидна; в загальному випадку …
4. Інтегрування нерівності. Якщо f1(x) f2(x), x( a, b ), то
![]() де
a
< b.
де
a
< b.
5. Оцінка модуля інтеграла
![]()
6.Теорема про середнє значення. Якщо f(x) неперервна на
[ a, b ], то c[ a, b ] таке, що
![]() (4.6)
(4.6)
Геометричне тлумачення теореми при f(x) 0 і f С[ a, b ] таке: криволінійна трапеція рівновелика з відповідним прямокутником, який має з трапецією спільну основу
( рис. 4.3 ).
Доведення.
Знеперервності f(x)
випливає обмеженість її на [a,b],
тобто існують m<M
такі, що m![]() f(x)
M
на [a,b].
Зінтегруємо останню нерівність
скориставшись власти-вістю 4.
. Маємо
f(x)
M
на [a,b].
Зінтегруємо останню нерівність
скориставшись власти-вістю 4.
. Маємо
![]() ,
,
або
![]() (4.6)
(4.6)
Звідси
![]() (4.7)
(4.7)
Нехай
![]() .
Беручи
до уваги теорему про найбільше, найменше
і проміжні значення неперервної функції
дійдемо висновку, що існує принаймі
одна точка
.
Беручи
до уваги теорему про найбільше, найменше
і проміжні значення неперервної функції
дійдемо висновку, що існує принаймі
одна точка
![]() така що
така що
![]() ,
тобто виконується рівність (4,6). Нерівність
(4,7) називають оцінкою визначеного
інтегралу для обмеженої функції За
допомогою цієї формули можна визначити
межі , в яких міститься величина інтеграла
, не обчислюючи його.
,
тобто виконується рівність (4,6). Нерівність
(4,7) називають оцінкою визначеного
інтегралу для обмеженої функції За
допомогою цієї формули можна визначити
межі , в яких міститься величина інтеграла
, не обчислюючи його.
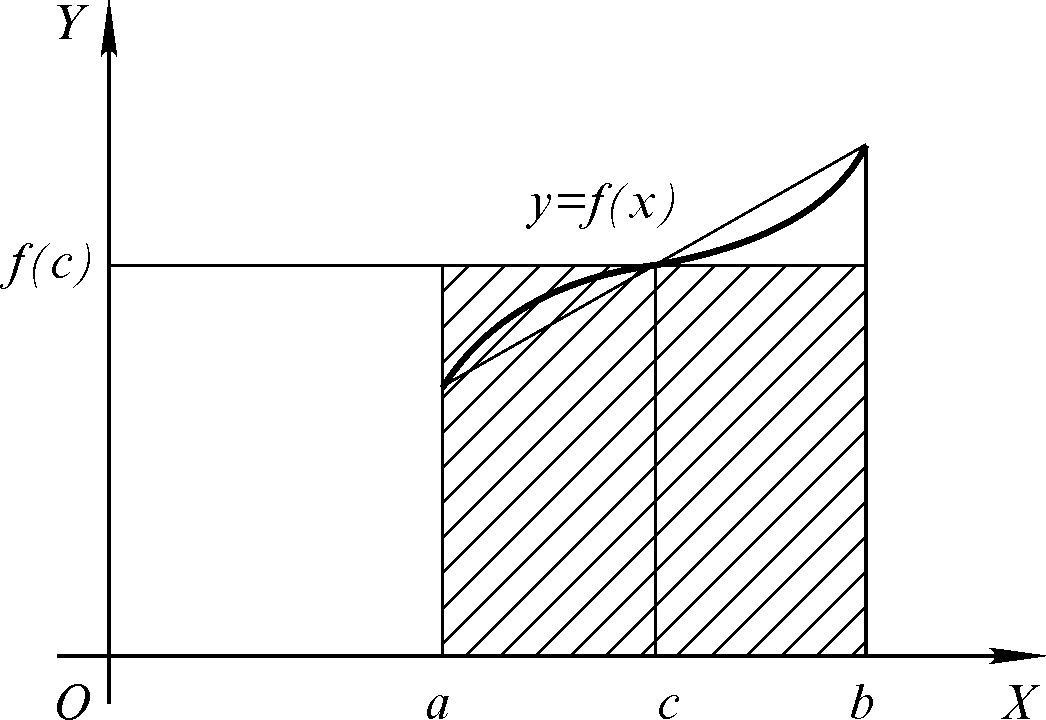
Рисунок 4.3
Означення.
Середнім значенням інтегрованої на
[a,b]
функції f(x)
називається
величина
![]() .
.
Деякі з цихвла стивостей випливають з означення (4.5), а доведення інших властивостей зрозумілі інтуїтивно
(властивість 1-6 довести самостійно)
4.4. Обчислення визначеного інтеграла за допомогою
невизначеного інтеграла.
Як
випливає з усього попереднього , в самій
математиці і її застосуванні надзвичайно
важливу роль відіграють два типи границь.
Один із них
![]() дає нам похідну,
дає нам похідну,
а
інший –![]()
-
визначений інтеграл від функції. Важливе
значення має теорема Барроу, яка
встановлює зв’язок
між цими двома поняттями. Її називають
основною теоремою диференціального і
інтегрального числення. Щоб перейти до
неі, розглянемо визначений інтеграл як
функцію від його верхньоі межі (інтеграл
із змінною верхньою межею)
-
визначений інтеграл від функції. Важливе
значення має теорема Барроу, яка
встановлює зв’язок
між цими двома поняттями. Її називають
основною теоремою диференціального і
інтегрального числення. Щоб перейти до
неі, розглянемо визначений інтеграл як
функцію від його верхньоі межі (інтеграл
із змінною верхньою межею)
![]() (4.8)
(4.8)
Ми
скористались тим, що
![]() .
.
Теорема (Барроу). Якщо f неперервна функція на [a,b] то Ф/(x)=f(x) ,тобто Ф(х) є первісною для інтегровної функції.
Доведення. Знайдемо похідну функції Ф(х), тобто
![]()
На основі властивості 3 дістаємо:
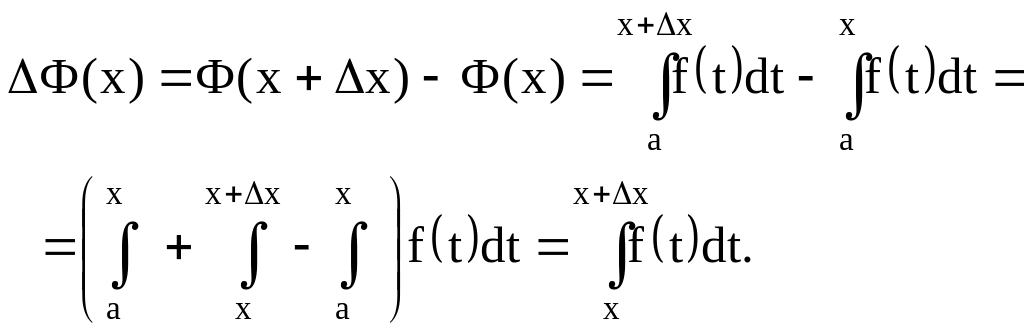
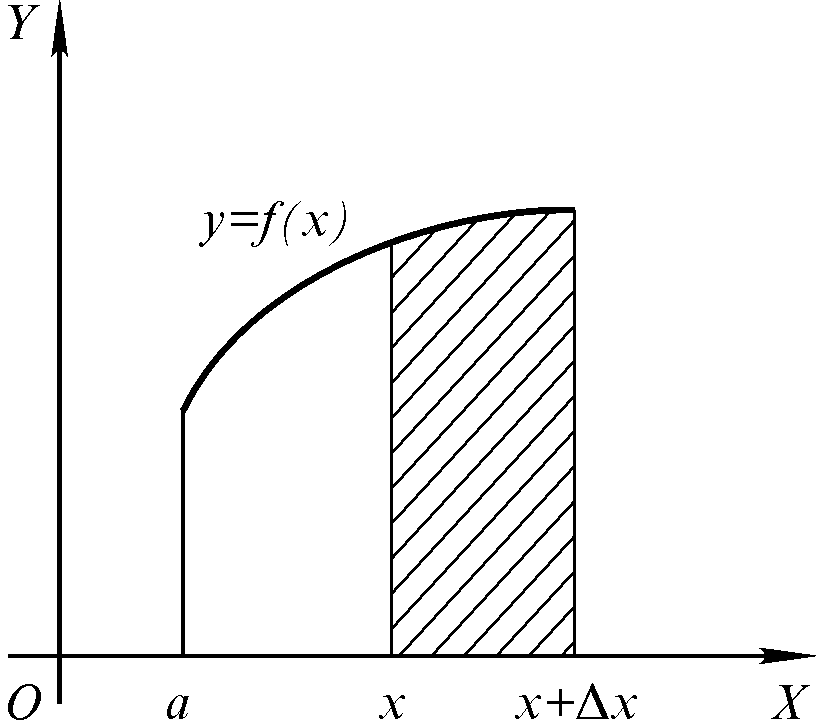
Рисунок 4.4
За теоремою про середнє значення
![]() .
.
Оскільки f(x) неперервна, то
![]() .
.
Отже, вираз (4.8) є первісною для неперервної функції y=f(x).Це випливає із означення первісної і теореми Барроу.
Теорема. Якщо функція F(x) є первісною для неперервної функції f(x), то
![]() (4.9)
(4.9)
Формулу (4.9) називають формулою Ньютона-Лейбніца, а іноді основною формулою інтегрального числення.
Доведення. За умовою F(x) є первісною для неперервної функції y=f(x), а Ф(х)– первісна за теоремою Барроу, тому F(x) і Ф(x) відрізняються лише на сталу:
![]() ,
тобто
,
тобто
![]() .
(4.10)
.
(4.10)
Нехай x=a в (4.10). Тоді
![]() ,
звідки
C=-F(a)
.
,
звідки
C=-F(a)
.
Нехай x=b. Тоді
![]() .
.
Наслідок. Справедливі формули
![]() і
і
![]() .
.
Приклади.
-
1.
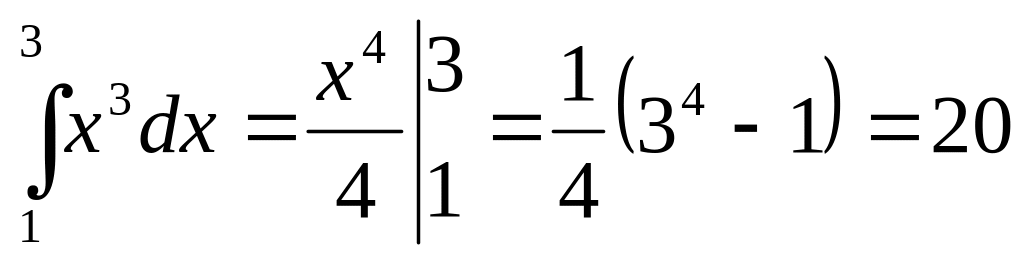 .
.2.
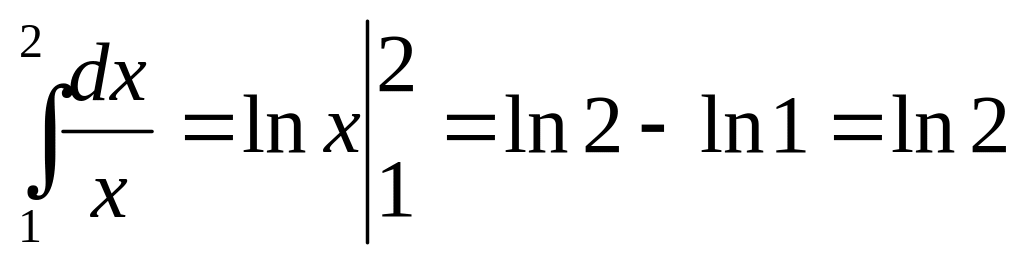
3.
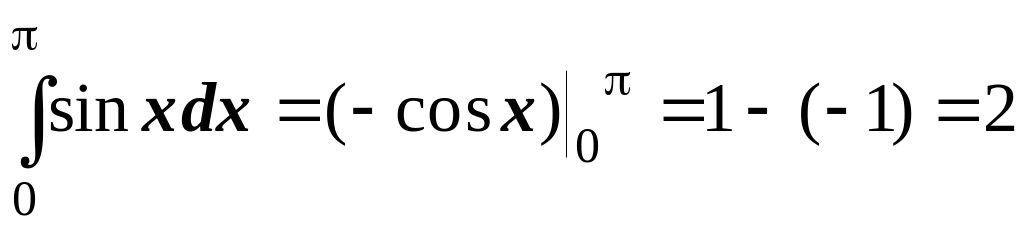
Вправи.
Користуючись формулою Ньютона-Лейбніца, обчислити інтеграли.
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
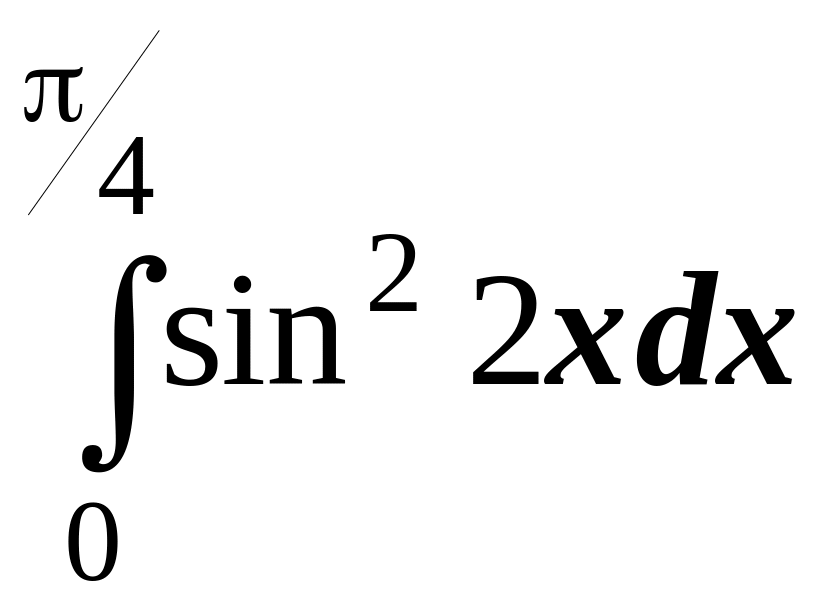 6.
6.
![]()
7.
![]() 8.
8.
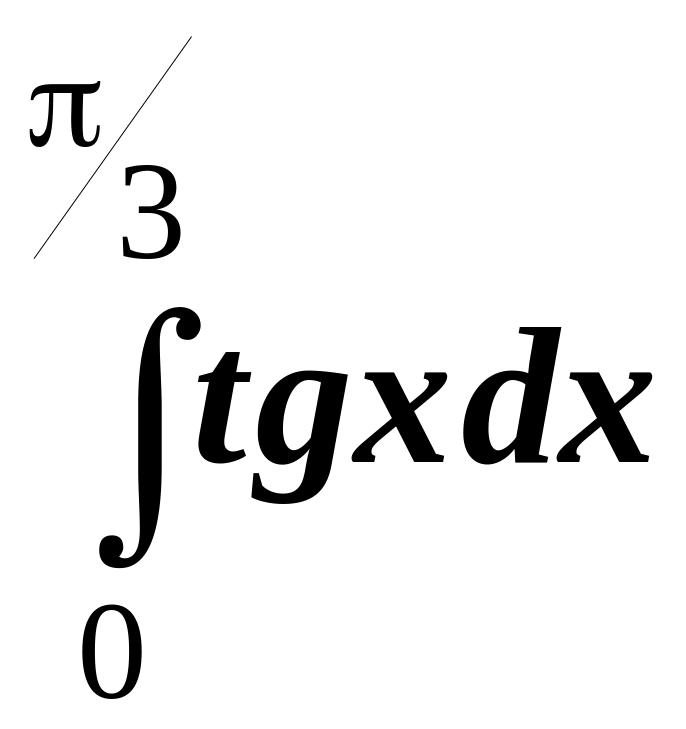 9.
9.
![]() 10.
10.
![]()
Відповіді:1)
48. 2) 25/ln
5. 3) 0,5(ln 13-ln 7). 4) 1,5. 5)
![]() .
6)
.
6)
![]() .
7)
.
8) ln2.
9) 1.
10)
.
7)
.
8) ln2.
9) 1.
10)
![]() .
.
Лекція 5
Методи обчислення визначеного інтеграла .
Невластиві інтеграли
Оскільки для знаходження визначеного інтеграла треба спочатку знайти невизначений інтеграл (первісну), а потім скористатися формулою Нютона-Лейбніца, то методи обчислення визначеного інтеграла збігаються з методами знаходження невизначеного інтеграла. Таких методів є два: заміна змінної та інтегрування частинами.
