
- •Лекція 1
- •1.1. Первісна
- •1.2. Невизначений інтеграл
- •1.3. Властивості невизначеного інтеграла
- •1.5. Основні методи інтегрування
- •Лекція 2 Інтегрування дробово - раціональних і деяких ірраціональних функцій
- •2.1. Інтегрування елементарних дробів
- •2.2. Інтегрування раціональних дробів
- •2.3. Інтегрування ірраціональних функцій
- •Приклад.
- •Приклад.
- •Лекція 3 Інтегрування тригонометричних функцій. Застосування невизначених інтегралів.
- •3.1 Інтегрування деяких тригонометричних функцій
- •Вправи. Обчислити інтеграли.
- •3.2 Застосування невизначенх інтегралів
- •Вправи.
- •Лекція 4 Визначений інтеграл
- •3.1. Приклади задач, які приводять до поняття визна-
- •3.3 Властивості визначеного інтеграла.
- •4.4. Обчислення визначеного інтеграла за допомогою
- •5.1. Інтегрування заміною змінної (метод підстановки)
- •5.2. Інтегрування частинами
- •5. Невластиві інтеграли
- •5.3 Невластиві інтеграли першого роду
- •Ознаки збіжності невластивих інтегралів першого роду.
- •5.4. Невластиві інтеграли другого роду.
- •6.1. Геометричні застосування інтеграла.
- •6.3. Обчислення об’ємів тіл.
- •Обчислення площ поверхонь обертання.
- •Теоретичні (екзаменаційні) питання.
2.3. Інтегрування ірраціональних функцій
Інтегрування деяких ірраціональних функцій за допомогою певних підстановок зводиться до інтегрування раціональних функцій. Якщо така підстановка існує, то казатимемо, що інтеграл раціоналізується.
I.Інтеграл виду
![]()
де
R
–
раціональна функція;
m1
,n1
,m2
,n2
….. – цілі
числа зводиться до інтегралу від
раціональної функції за допомогою
підстановки
![]() ;
s
–найменше
спільне кратне чисел n1
,
n2
….
;
s
–найменше
спільне кратне чисел n1
,
n2
….
Приклад . Обчислити інтеграл.
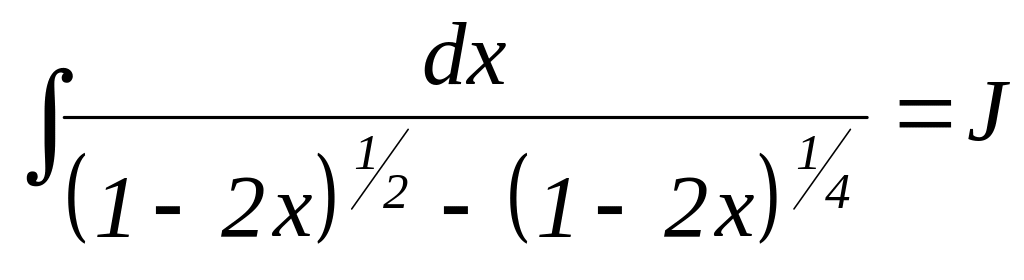
Розв’язання.
Тут n1
=2,n2
=4,
а тому s=4.
Використаємо
підстановку
![]() ,
,
тоді
![]() і , dx
= -2t3dt,
тому
і , dx
= -2t3dt,
тому
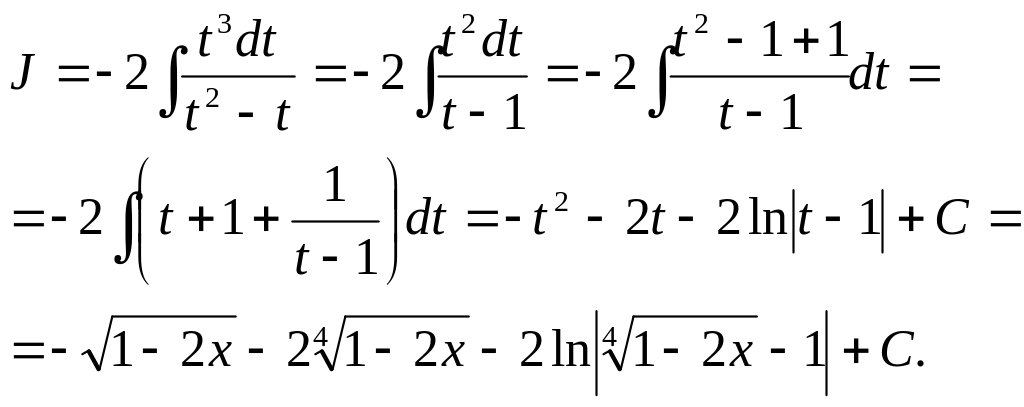
II.
Інтеграли
виду
![]() зводять
до таблич-них інтегралів виділенням
повного квадрату у тричлені
зводять
до таблич-них інтегралів виділенням
повного квадрату у тричлені
![]()
і
наступною заміною змінної
![]()
Приклад.
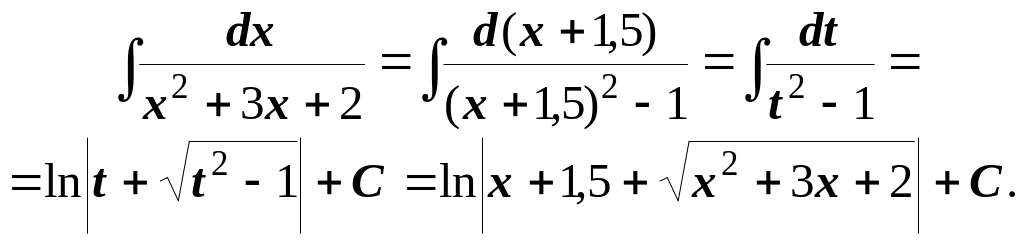
Інтеграли виду

обчислюють так: у чисельнику дробу записують похідну квадратного тричлена, що міститься під знаком кореня, і розбивають дріб на два дроби , перший з яких інтегрують за формулою(2.5), а другий зводять до випадку II.
Приклад.
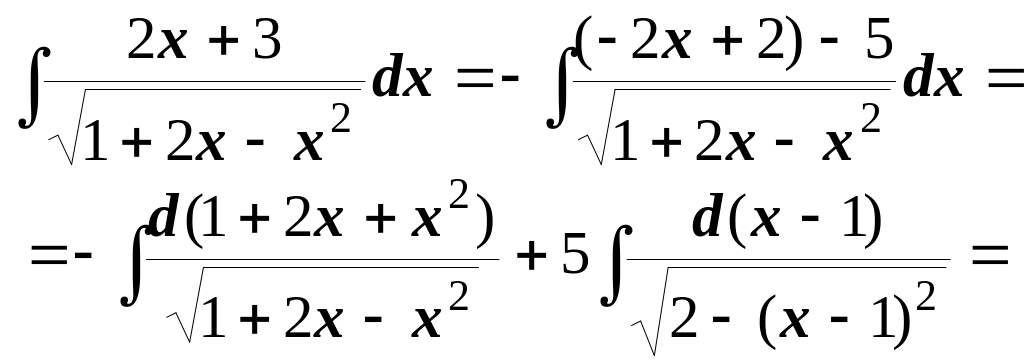
![]()
(перший інтеграл - згідно з формулою (2.7), а другий – формулою (15)табл. інтегралів)
IV.
Інтеграли виду
![]() за допомогою підстановки
за допомогою підстановки
![]() зводяться до випадку II.
зводяться до випадку II.
Приклад.
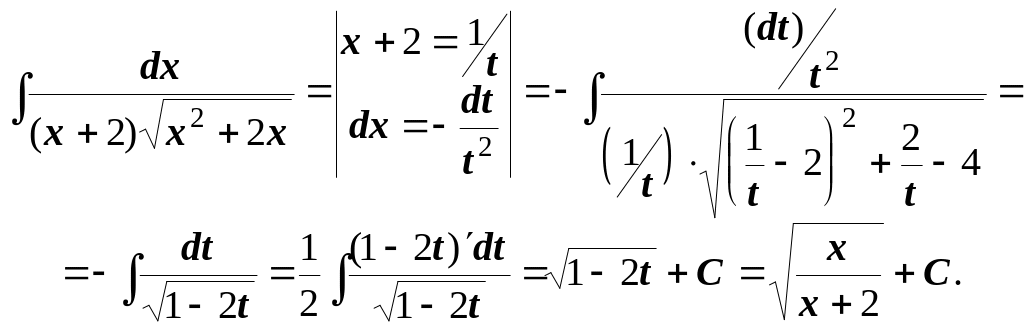
V. Інтегрування диференціальних біномів
![]() де
m
,n
,p
– раціональні
числа .
де
m
,n
,p
– раціональні
числа .
П.Л.Чебешев довів, що інтеграли такого типу виражаються через елементарні функції в лише трьох випадках за допомогою відповідних підстановок:
1) p – ціле число, тоді підстановка x = t s, де s- найменше спільне кратне знаменників чисел m i n;
2)
![]() –
ціле число, підстановка
–
ціле число, підстановка
![]()
де s- знаменник числа P;
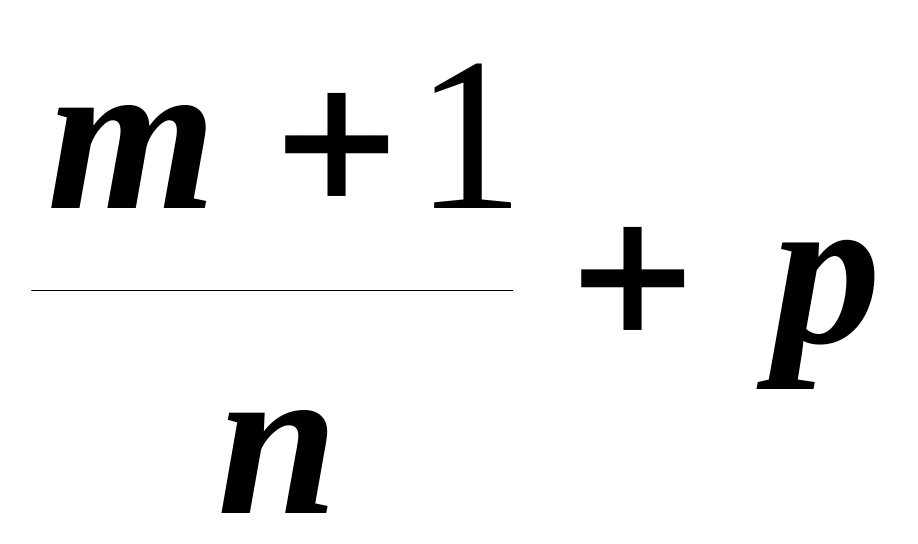 –
ціле
число, підстановка
–
ціле
число, підстановка
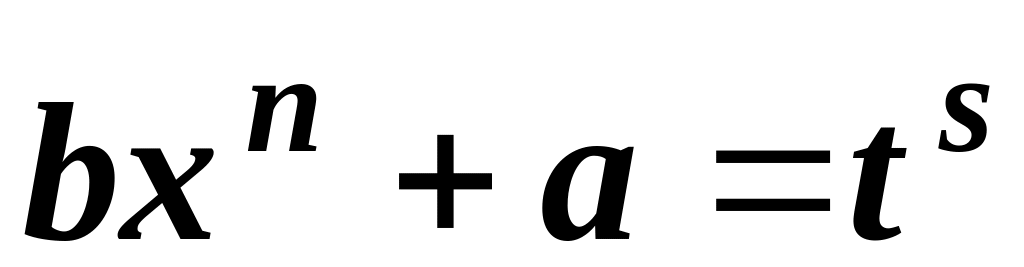
або![]() ,
де s-
знаменник числа p;
,
де s-
знаменник числа p;
Приклади. Обчислити інтеграли.
1)
![]()
Розв’язання. Запишемо підінтегральну функцію у вигляді
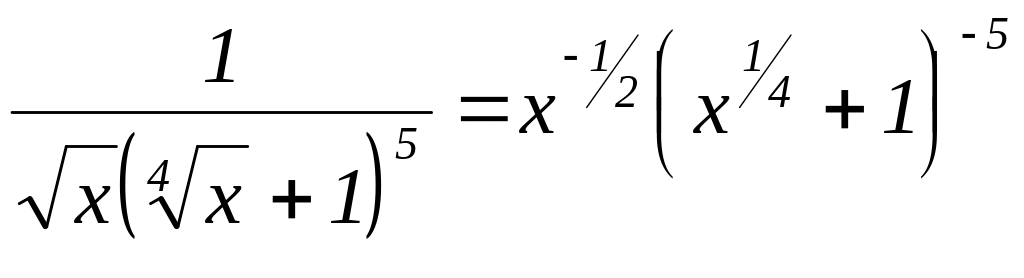
Маємо перший випадок диференціального бінома
(p
= -5). Застосуємо першу підстановку
![]() ;
;![]() .
.
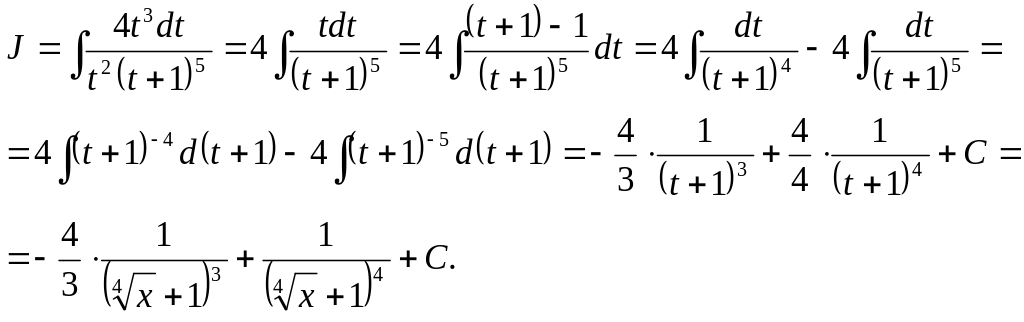
2)
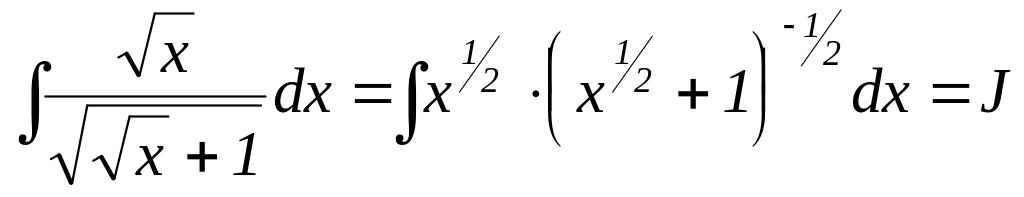 .
.
Розв’язання.
Тут
![]() ,
,
![]() ,
,
![]() .
.
Оскільки = 3 – ціле, то застосуємо другу підстановку
![]() ,
тоді
,
тоді
![]() ,
тоді
,
тоді
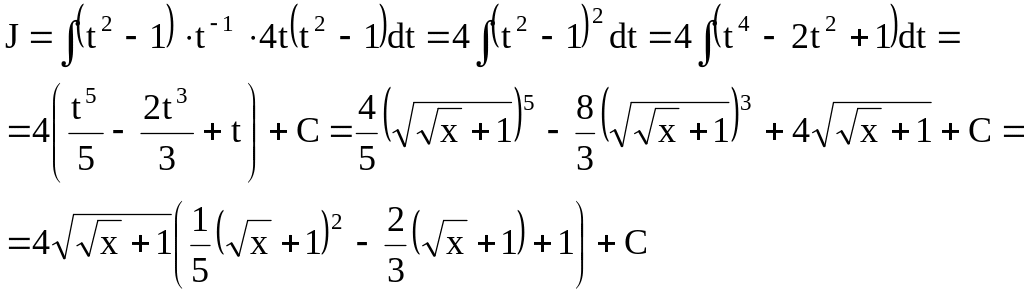
3)
![]()
Розв’язання. Оскільки = 1 – ціле, застосо-вуємо третю підстановку.
4x3+3=x3t2,
тоді
![]()
Інтеграл набуває вигляду
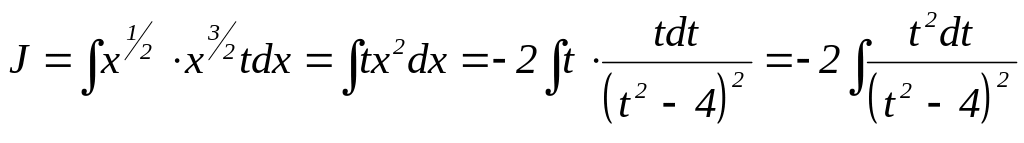
Застосуємо метод інтегрування частинами.
Покладемо
u=t,
dv=![]() ,
тоді
,
тоді
du=dt;
![]() й, маємо
й, маємо
![]() При
умові, що
При
умові, що
![]() .
.
Отже
![]()
Вправи.
Обчислити інтеграли.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]()
Відповіді.
1.
![]() .
2.
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
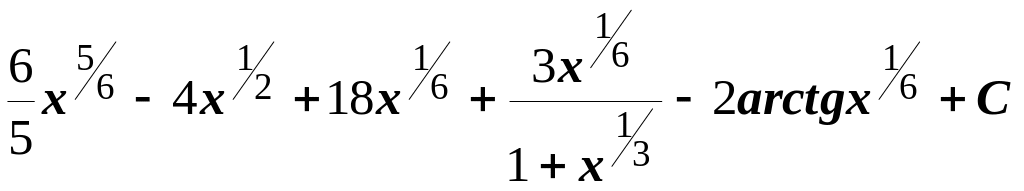 .
.
6.
![]() де
де
![]() .
.
7.
![]() .
.
Лекція 3 Інтегрування тригонометричних функцій. Застосування невизначених інтегралів.
3.1 Інтегрування деяких тригонометричних функцій
1.
Інтеграли
![]() ,
де R–раціональна
функція своїх аргументів, зводять до
інтегралів
від раціо-нальних функцій нової змінної
t за допомогою підстанов-ки
,
де R–раціональна
функція своїх аргументів, зводять до
інтегралів
від раціо-нальних функцій нової змінної
t за допомогою підстанов-ки
![]() .
Її називають універсальною тригонометрич-ною
підстановкою.
.
Її називають універсальною тригонометрич-ною
підстановкою.
Дійсно, врахувавши, що
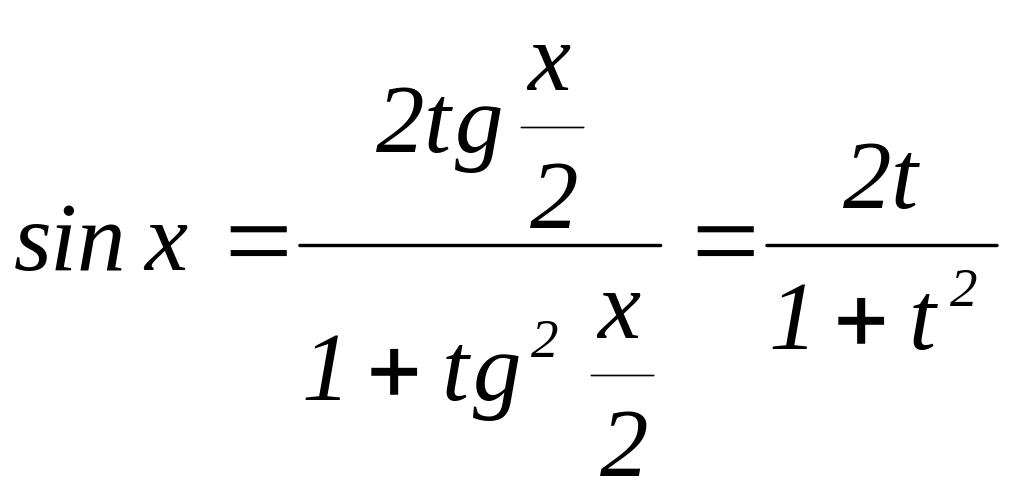
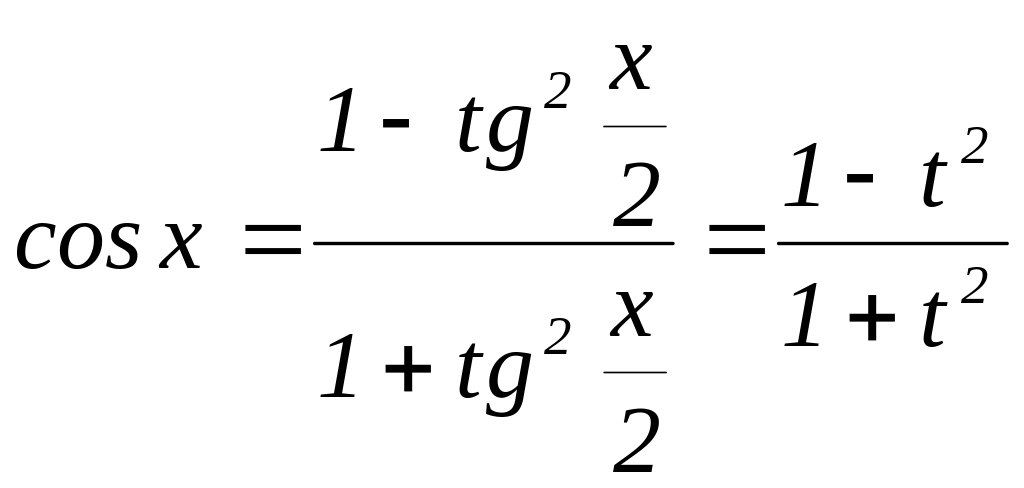
![]()
![]()
маємо:
![]()
Приклад.
![]() .
.
Покладемо![]() .
Тоді
.
Тоді
![]() ,
,
![]() і
і
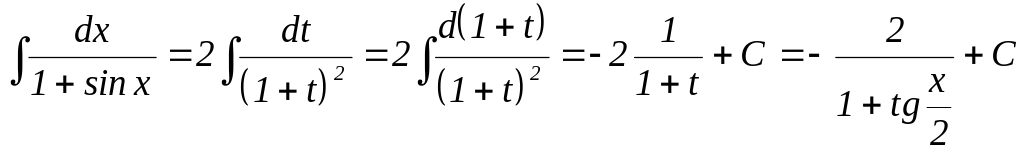
Зауважимо,
що хоча при інтегруванні функцій виду![]() можна завжди перейти до інтегрування
раціональних функцій за допомогою
універсальної підстановки, але така
раціональна функція може привести до
досить громіздких викладок, тому варто
попередньо перевірити, чи не можна
застосувати інший метод або підстановку,
яка допоможе спростити обчислення
інтеграла. У деяких окремих випадках
обчислення інтегралів такого виду може
бути спрощено.
можна завжди перейти до інтегрування
раціональних функцій за допомогою
універсальної підстановки, але така
раціональна функція може привести до
досить громіздких викладок, тому варто
попередньо перевірити, чи не можна
застосувати інший метод або підстановку,
яка допоможе спростити обчислення
інтеграла. У деяких окремих випадках
обчислення інтегралів такого виду може
бути спрощено.
1). Якщо R(sin x, cos x) – непарна функція відносно sinx, тобто якщо R(-sinx, cosx)= -R(sinx, cosx), то інтеграл раціоналізує підстановка cosx=t;
2). Якщо R(sinx, cosx) – парна функція відносно cosx,
тобто якщо R(sinx;-cosx)= -R(sinx,cosx), то інтеграл раціоналізує підстановка sinx=t;
3). Якщо R(sinx, cosx) – непарна функція відносно
sinx і cosx, тобто якщо R(-sinx;-cosx)=R(sinx,cosx), то інтеграл раціоналізує підстановка tgx=t.
Приклад.
![]()
У
цьому випадку підінтегральна функція
непарна відносно cosx;
використаємо підстановку sinx=t;
тоді
![]() і
і
![]() .
.
Маємо
![]()
![]()
![]()
2.
Інтеграл виду
![]() ,
де m,n
Z, обчислюють
так. Якщо n–непарне
додатне число, то зас-тосовується
підстановка sinx=t,
а якщо m
– непарне
додат-не число, то підстановка cosx=t.
Якщо m і
n–
парні неві-д’ємні числа, то пониження
степеня здійснюється через пе-рехід
до подвійного аргумента за допомогою
тригономет-ричних формул:
,
де m,n
Z, обчислюють
так. Якщо n–непарне
додатне число, то зас-тосовується
підстановка sinx=t,
а якщо m
– непарне
додат-не число, то підстановка cosx=t.
Якщо m і
n–
парні неві-д’ємні числа, то пониження
степеня здійснюється через пе-рехід
до подвійного аргумента за допомогою
тригономет-ричних формул:
![]() ;
;
![]() ;
;
![]() .
.
Приклад 1.
![]()
Маємо m=3 – непарне додатнє число. Відокремлючи один співмножник від sin3x, дістанемо
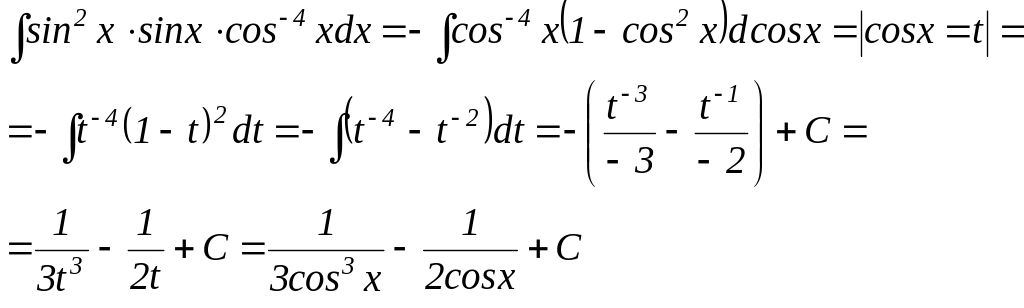
Приклад 2.
![]() .
У цьому випадку m=n=2,
тоді
.
У цьому випадку m=n=2,
тоді
![]() .
.
Отже,
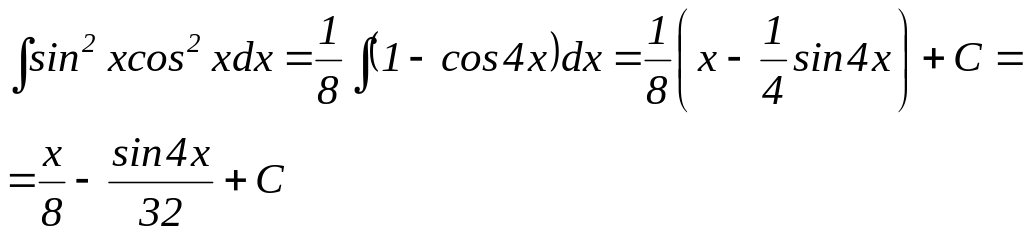
3.
Інтеграли
виду
![]() ,
,
![]() ,
,
![]() ,
обчислюють,
ви-користовуючи формули:
,
обчислюють,
ви-користовуючи формули:
![]()
![]()
![]()
Приклад.
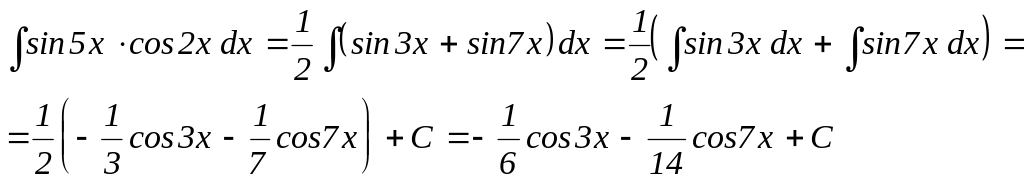
4.
Інтеграл виду
![]() і
і
![]() ,
де m –
ціле
додатне
число. Для обчислення таких інтегралів
вико-
,
де m –
ціле
додатне
число. Для обчислення таких інтегралів
вико-
ристовують
відомі формули:
![]() і
і
![]() ,
за допомогою яких поступово змен-шують
степінь тангенса чи котангенса.
,
за допомогою яких поступово змен-шують
степінь тангенса чи котангенса.
Приклад 1.
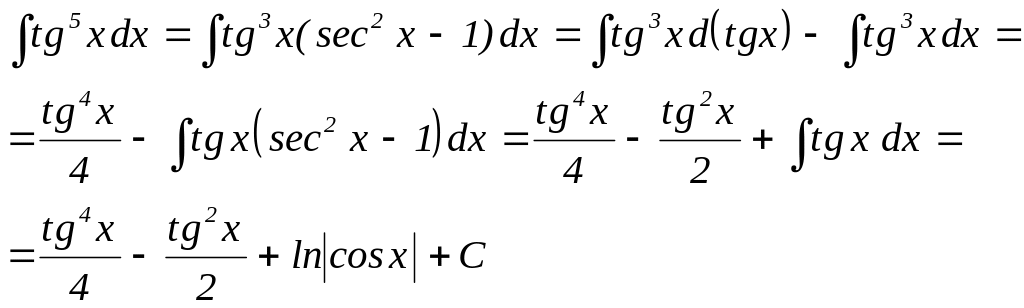
Приклад 2.
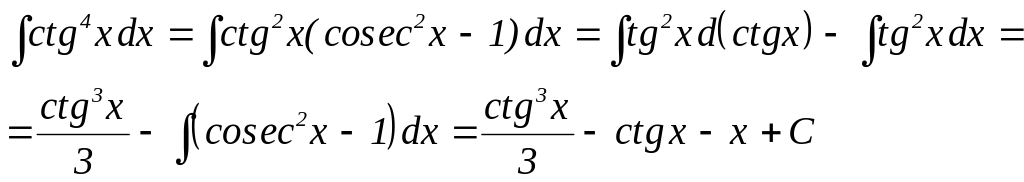
5.Інтеграли
вигляду
![]() і
і
![]() де n –
додатне парне число. Інтеграли обчислюють
(аналогічно попереднім) за до-помогою
формул
де n –
додатне парне число. Інтеграли обчислюють
(аналогічно попереднім) за до-помогою
формул
![]() і
і
![]() .
.
Приклад.
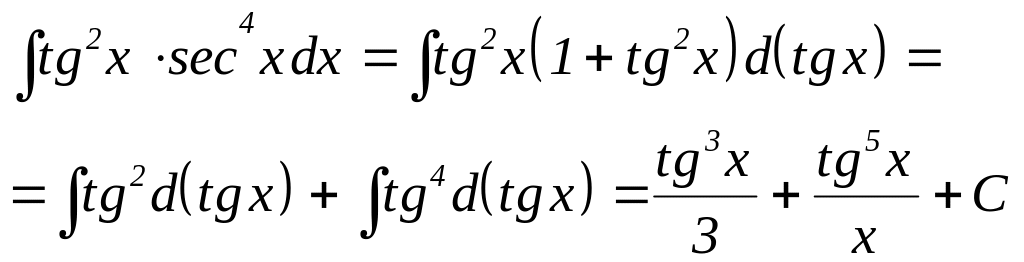
6.
Інтеграли виду
![]() і
і
![]() обчислюють за допомогою рекурентних
формул
обчислюють за допомогою рекурентних
формул
![]() ,
,
![]()
Приклад.
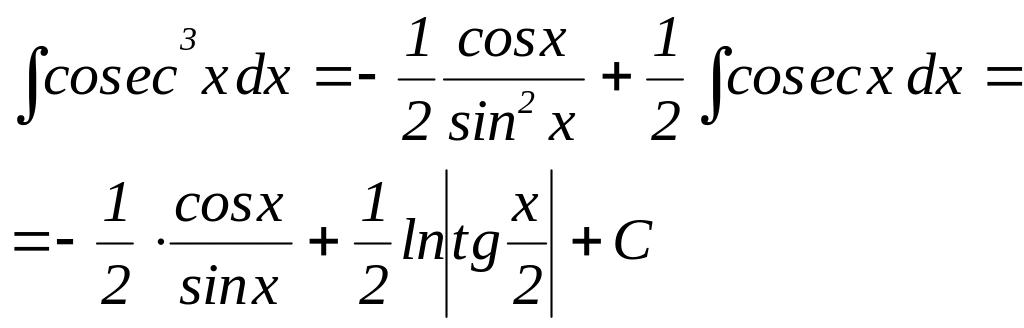
7.Тригонометричні підстановки.
Інтеграли виду
![]()
![]()
![]()
зводяться до інтегралів від раціональних функцій відносно косинуса і синуса за допомогою тригонометричних підста-новок, відповідно:
x=a·sin t (або x=a·cos t);
x=a·tg t (або x=a·ctg t);
x=a·sec t (або x=a·cosec t).
Приклад.
![]() .
.
Обчислимо
цей інтеграл
за допомогою підстановки x=a·cosect;
тоді
![]() і
і
![]() .
Маємо
.
Маємо
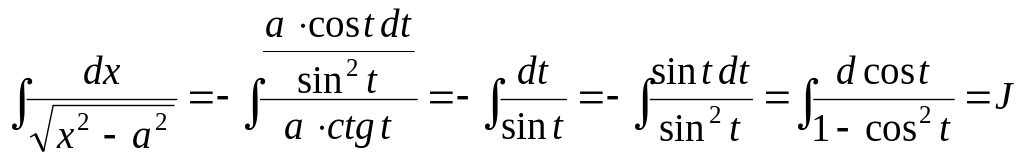
Покладемо cos t=u .Тоді інтеграл
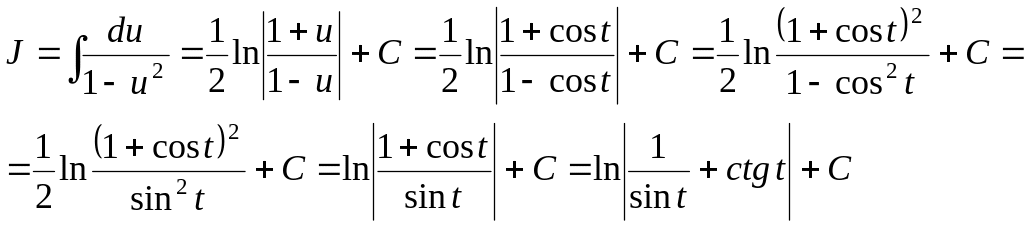
Повертаючись до змінної x дістанемо
![]()
де C1 = C - ln a. Отже:
![]()
