Лекція 2 Інтегрування дробово - раціональних і деяких ірраціональних функцій

Функція вигляду , де P(x) і Q(x) – многочлени, називається дробово - раціональною, або просто дробом. Дріб правильний, якщо степінь многочлена P(x) нижчий за степінь Q(x). В іншому випадку дріб неправильний. Якщо дріб неправильний, з нього виділяють цілу частину (многочлен), ділячи чисельник на знаменник:

Правильний дріб можна подати у вигляді суми скінченного числа елементарних дробів.

2.1. Інтегрування елементарних дробів

Елементарними дробами називаються правильні дроби такого вигляду:

I. ;II. ;III. IV.

де 2 n  N, p²-4q< 0; A,B,a,p,qR.

Ці дроби відповідно називають елементарними дробами I, II, III і IV типів. Інтеграли від елементарних дробів обчислюємо за формулами:

I.

2. 

III.

Якщо чисельник дробу пропорційний похідній знаменника, то інтеграл обчислюємо за формулою ( 27). В іншому разі чисельник розкладається на суму двох доданків, один з яких пропорційний похідній тричлена, а другий сталий

Тоді

Перший інтеграл

а інтеграл

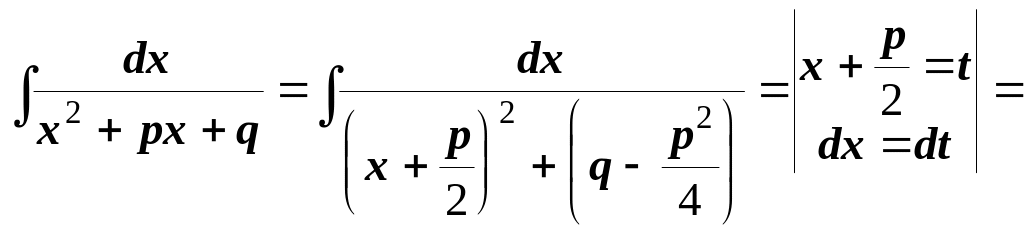
Отже,

Приклад.

IV. Розглянемо інтегрування елементарних дробів IV типу. Як і в попередньому випадку, запишемо

Перший інтеграл у правій частині легко знаходимо за допомогою підстановки x²+px+q=t , а другий запишемо так:

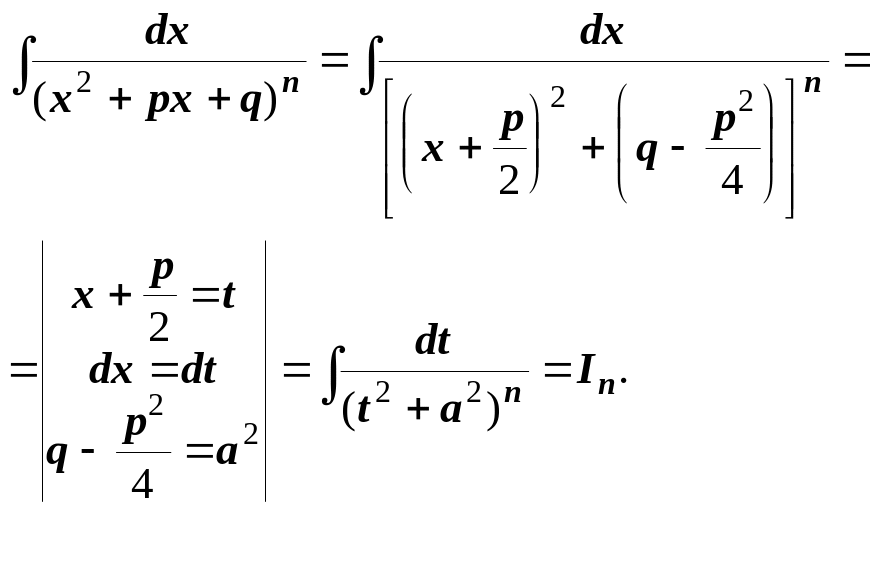
Останній інтеграл (n-1) кратним інтегруванням зводиться до табличного за допомогою рекурентної формули

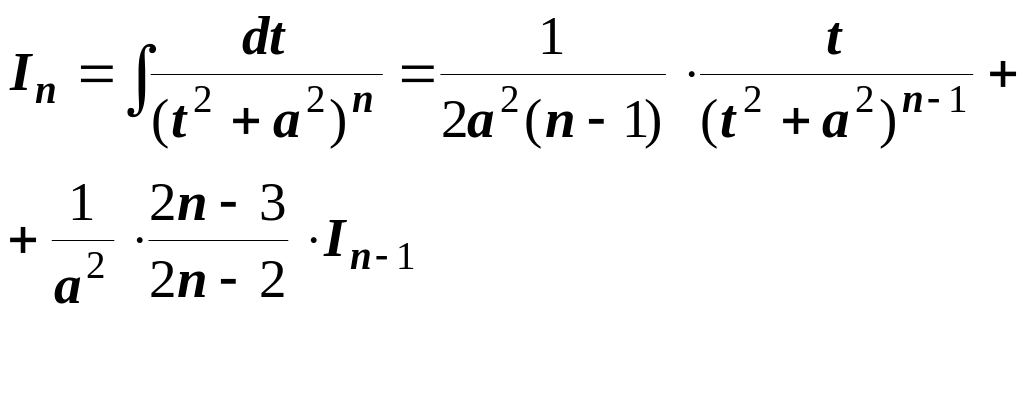(2.1)

Приклад. Знайти інтеграл.

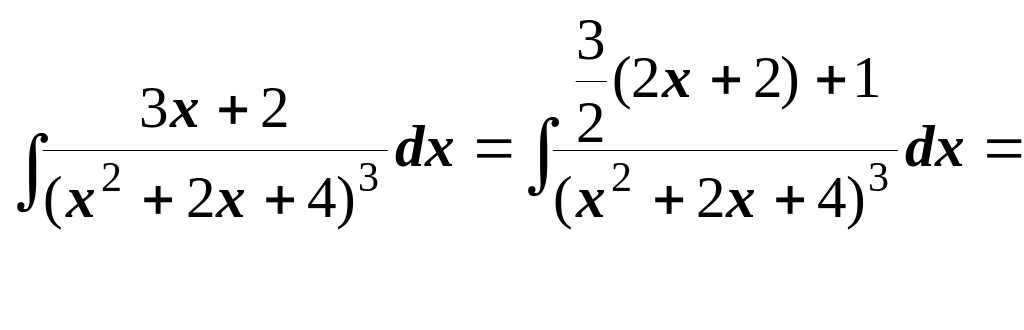
Розв’язання. В першому інтегралі зробимо заміну x²+2x+4=z, (2x+2)dx=dz, а в другому x+1=t, dx=dt. Тоді

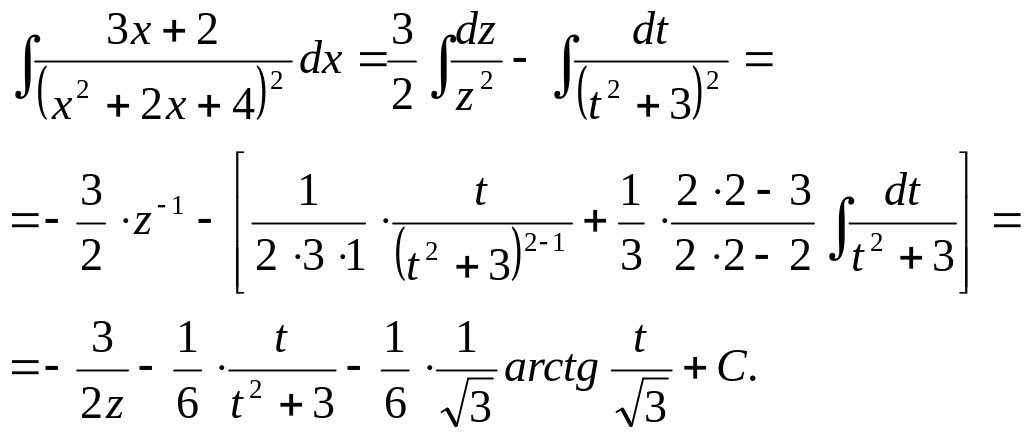
Повернувшись до змінної x, дістаємо:

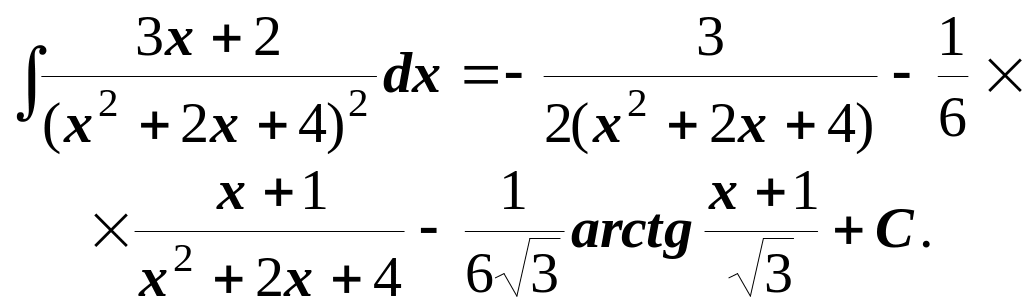
2.2. Інтегрування раціональних дробів

Інтегрування кожного раціонального дробу можна звести до інтегрування суми елементарнх дробів за схемою:

1) Якщо дріб неправильний (mn), то виділивши цілу частину, записати його у вигляді

, де r<n; R_n-m(x)–многочлен степеня (n-m), а – правильний раціональний дріб;

2) розкласти знаменник дробу на лінійні і квадратичні множники

,

де p²-4q<0 , тобто тричлен x²+px+q має комплексні спряжені корені;

3. дріб зобразити у вигляді суми елементарних дробів:

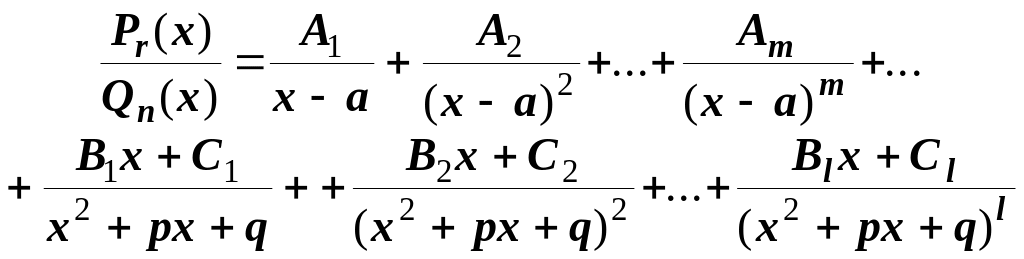
де A₁,A₂,...,A_m ,B₁ ,C₁ , B₂ ,C₂ ..., B_l ,C_l ,... –деякі сталі (невизначені коефіцієнти); m,..l,..– натуральні числа, причому m+..+2l+...=n (поясніть чому).

4) обчислити невизначені коефіцієнти. Для цього необхідно звести останню рівність до спільного знаменника і прирівняти чисельники в обох частинах рівності. Невідомі коефіцієнти обчислюють двома способами: 1)прирівнянням коефіцієнтів при однакових степенях змінної в обох частинах рівності; 2) наданням змінній конкретних значень. Часто застосовують комбінацію цих способів. При цьому дістанемо систему n лінійних рівнянь з n невідомими A₁ ,A₂ ...

5) обчислити заданий інтеграл, використовуючи схему розкладу і значення невідомих коефіцієнтів.

Приклад . Обчислити інтеграл.

Розв’язання. Зобразимо підінтегральний вираз, який є правильним раціональним дробом, у вигляді суми елемен-тарних дробів :

.

Останню рівність зведем до спільного знаменника і прирівняємо чисельники

Оскільки число 1 є коренем знаменника,то, підставив-ши x=1, дістаємо 5=5A₂ , звідки A₂=1.

Для визначення A₁, B, C, прирівнюємо коефіцієнти при однакових степенях x:

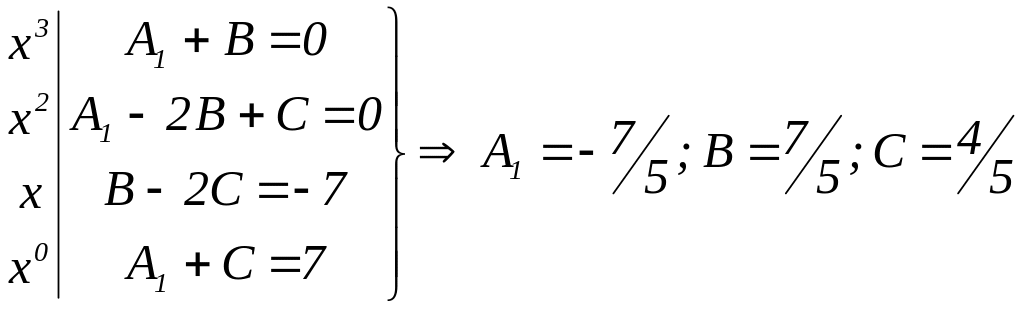
Обчислюємо заданий інтеграл, враховуючи значення знайдених коефіціентів і попередній розклад: