Обчислення площ поверхонь обертання.
Нехай маємо дугу АВ , що є графіком функції y=f(x) визначеної, невідємної і неперервної на відрізку a;b
(рис.6.21а).
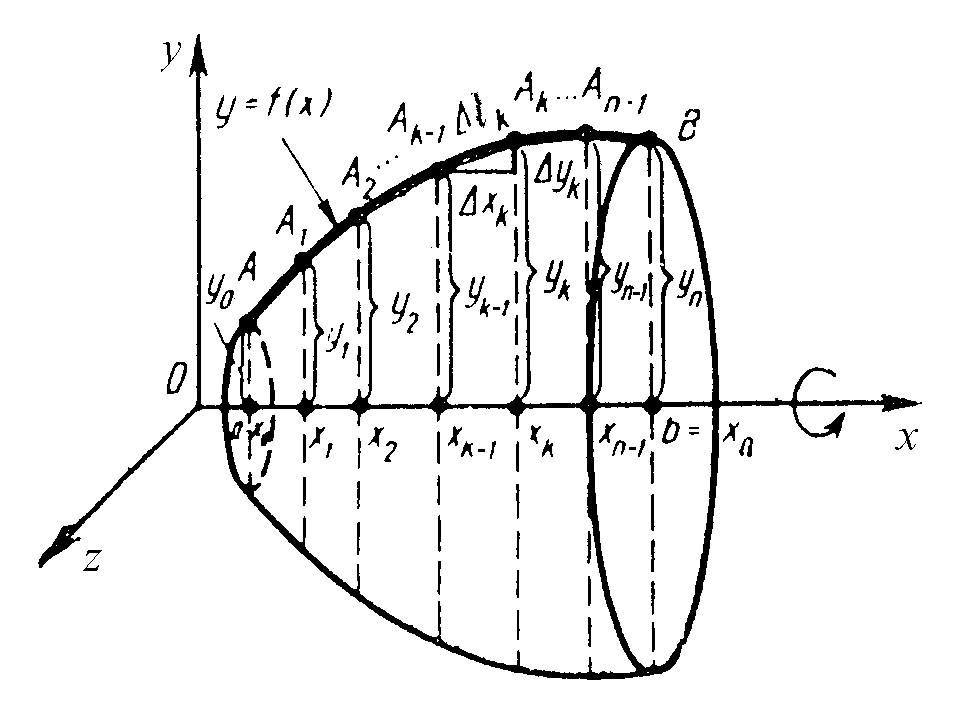
Рисунок 6.21а
Цю дугу як тверде тіло обертатимемо навколо осі Ох. Поверхня, яку опише при цьому дуга, називається поверхнею обертання. Розібємо дугу АВ довілиним чином на частини. Впишемо в дугу АВ ламану А0 А1 А2 ... Аn (АА0, ВАn), як і при обчисленні довжини дуги плоскої кривої.
При обертанні дуги АВ навколо осі Ох обертати-муться навколо цієї осі також ланки Ак Ак+1 (к=0,1,2,..., n-1) ламаної, кожна з яких описує бічну поверхню у загальному випадку зрізаного конуса (циліндра) (рис.21б).
Означення. Площею поверхні, утвореної обертанням даної лінії, називається границя поверхні, утвореної обертанням вписаної в цю лінію ламаної за умови, що число ланок ламаної прямує до нескінченності, а довжина кожної з них - до нуля.
Нехай Sk - поверхня зрізаного конуса (рис. 6.21б).
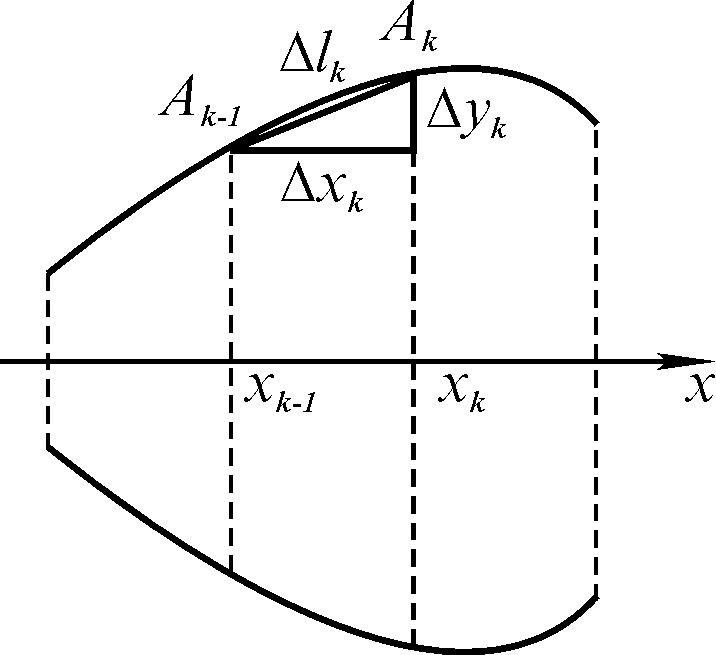
Рисунок 6.21б
Тоді
Sk
xk
Перейдемо до границі при d=max xk 0. Вважаючи відповідну суму інтегральною, дістанемо
(6.17)
Приклад. Знайти площу поверхні сфери з радіусом R
Розв’язання.Поверхню
сфери дістанемо в результаті обертання
навколо осі Ох
півкола
,
-R
x
R
. Отже,
Зауважимо, що коли крива x= (y) обертається навколо осі Оy ( - неперервна і має неперервну похідну / на відрізку c;d), то площу поверхні обертання обчислимо за формулою
(6.18)
Приклад.
Знайти площу поверхні обертання,
утвореної обертанням навколо осі Оу
частини параболи
,
відрізаної прямою
(рис.6.22).
Розв’язання.
Маємо
. за формулою (6.18) дістанемо
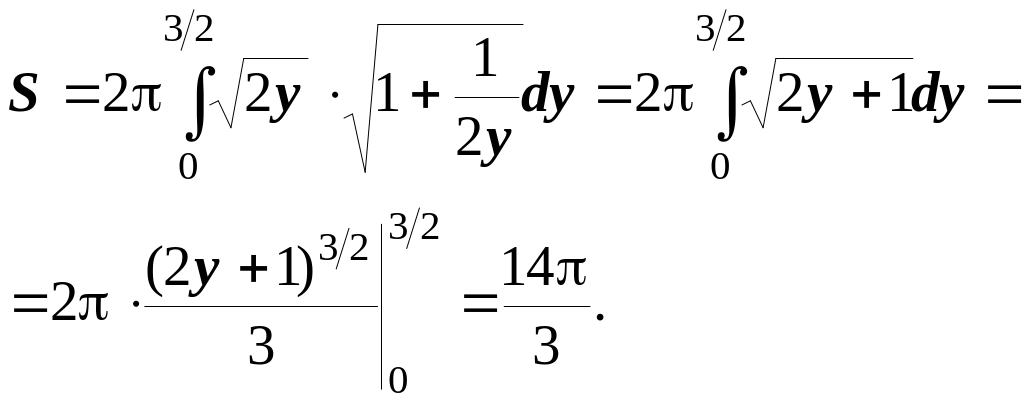
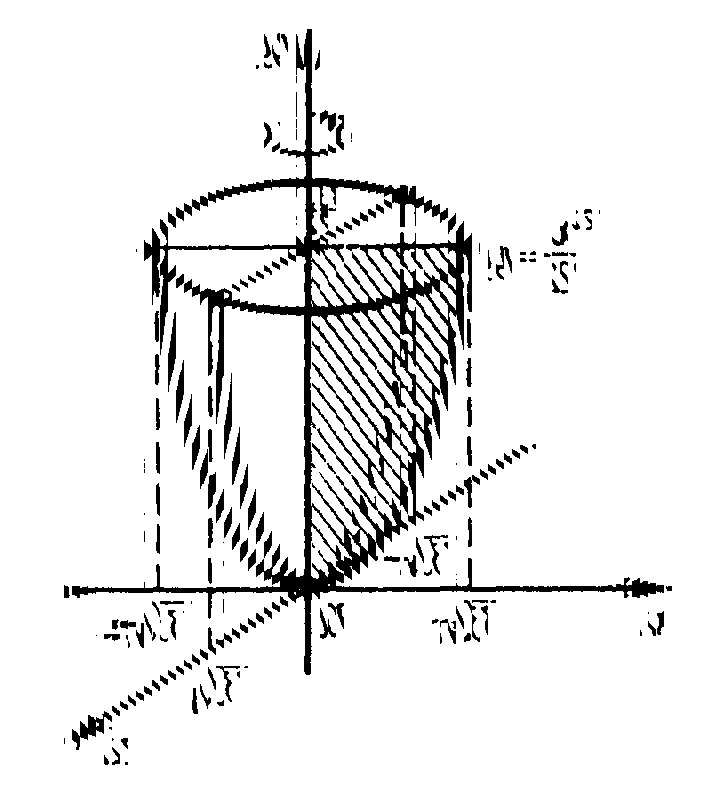
Рисунок 6.22
Вправи.
1. Знайти об’єм конуса з радіусом основи R і висотою H.
2.
Обчислити обєм тіла, обмеженого еліптичним
параболоїдом
і площиною z
=1.
3.
Обчислити об’єм тіла, обмеженого
однопорожнинним гіперболоїдом
і площинами z=-2;
z=1.
4.
Знайти об’єм
еліпсоїда, утвореного обертанням еліпса
навколо осі Ох.
5. Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями 2y=x2 і 2x+2y-3=0.
Знайти об’єм тіла, утвореного обертанням навколо
осі
Оу
фігури, обмеженої лініями
i
y=2.
7.
Знайти площу поверхні, утвореної
обертанням кривої
навколо осі Ох.
8.
Знайти площу поверхні, утвореної
обертанням кривої
навколо осіОу.
Відповіді.
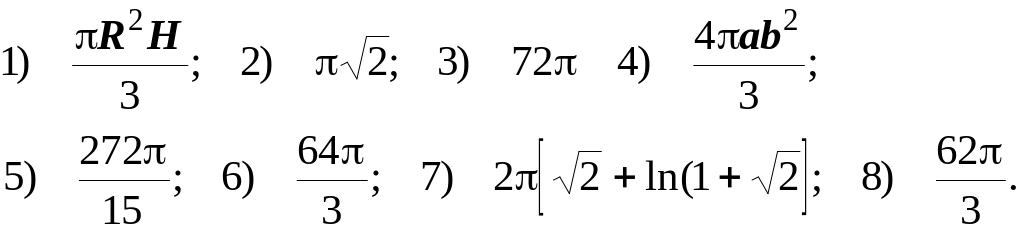
Теоретичні (екзаменаційні) питання.
1. Поняття первісної функції(означення, приклади,
властивості).
2. Поняття невизначеного інтеграла (означення,приклади).
3. Основні властивості невизначеного інтеграла.
4. Основні методи інтегрування: безпосереднє інтегрування; метод підстановки (заміни змінної); інтегрування частинами.
5. Елементарні раціональні дроби та їх інтегрування.
6. Інтегрування правильних раціональних дробів (метод невизначених коефіцієнтів).
7. Інтегрування виразів, які містять тригонометричні функції:
а)
б)
в)
(універсальна тригонометрична
підстановка).
Знаходження інтегралів виду:
а)
б)
в)
За допомогою тригонометричних підстановок.
9. Інтегрування деяких ірраціональних функцій.
Інтегрування деяких виразів, що містять квадратний
тричлен:
11. Задачі, які приводять до поняття визначеного інтеграла (площа криволінійної трапеції; робота змінної сили; маса прямолінійного стержня).
12. Означення й тлумачення визначеного інтеграла.
13. Властивості визначеного інтеграла. Теорема про середнє для визначеного інтеграла.
14. Визначений інтеграл із змінною верхньою межею інтегрування.
15. Теорема про існування первісної функції.
16. Формула Ньютона - Лейбніца (основна формула інтегрального числення).
17. Методи обчислення визначеного інтеграла: заміна змінної; інтегрування частинами.
18. Невластиві інтеграли першого роду.
19. Невластиві інтеграли другого роду.
20. Застосування визначеного інтеграла (обчислення площ фігур; довжин дуг; об’ємів тіл; площ поверхонь обертання).