6.1. Геометричні застосування інтеграла.

1. Обчислення площ плоских фігур.

а) Випадок прямокутних координат.

З геометричного тлумачення визначеного інтеграла для площі S криволінійної трапеції (рис.6.1) маємо форму-лу

S= (6.1)

Рисунок 6.1

Якщо f(x)0 (рис. 6.2), то аналогічно маємо

S= - (6.2)

Рисунок 6.2

У випадку, коли f(x) змінює знак на [a,b] (рис.6.3), то

S= (6.3)

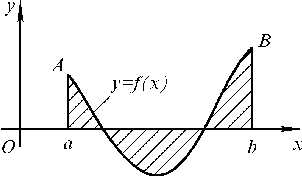
Рисунок 6.3

Очевидно, що (6.3) є загальною формулою д ля всіх розглянутих умов.

Нехай дві функції f(x) i g(x) визначені та непе-рервні на [a,b] і такі, що для всіх x[a,b]. Фігура, обмежена графіками цих функцій і , можливо відрізками прямих х=a й х=b, ординати точок яких змінюються відповідно від g(a) до f(a) та від g(b) до f(b), називається криволінійною трапецією, породженою графіками функцій f i g (рис.6.4). Площа такої трапеції оючислюється за формулою

(6.4)

Рисунок 6.4

Опрацюйте це самостійно.

Для обчислення площі складнішої фігури треба розбивати всю фігуру на частини відомого типу, знайти площі цих частин і результати додати.

Приклади.

1. Знайти площу S чверті круга з радіусом r.

Розв’язання.Розглянемо цю частину круга як криволінійну трапецію, породжену графіком функції y= , x[0,r]. За допомогою (6.1) дістаємо:

y

Рисунок 6.5

2. Обчислити площу S фігури, обмеженої лініями y=e^x,y=e^-x та x=ln5

Розв’язання.Точка перетину лінії y=e^x і y=e^-x має абсцису х=0. Тому шукана площа S (рис.6.6) обчислюється за формулою(6.4):

У випадку криволінійної трапеції, обмеженої лінією

y=y(t), x=x(t), де , тобто заданою параметрично, враховуючи (6.3), маємо:

S= (6.5)

Рисунок 6.6

3. Обчилити площу фігури , межею якої є крива, задана параметрично x=acos³t, y=asin³t, де 0t2 .

Розв’язання. Дана крива є астроїдою (рис. 6.7).

Рисунок 6.7

За формулою (6.4) маємо:

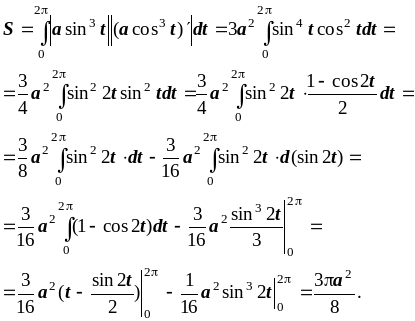
б) Випадок полярних координат

Нехай треба знайти площу криволінійного трикутника, обмеженого лініями =, =, =() (рис. 6.8)

Рисунок 6.8

Розіб’ємо [,] на n частин. Для [_i-1, _і], вважа-тимемо, що ()=const=(_і^*) для довільного _і^*[_i-1, _і]. Тоді площа відповідного сектора:

S_i=

Отже,

; ,

де =max_і. Тоді

(6.6)

Приклад. Обчислити площу фігури, обмеженої лемніскатою =a

Розв’язання. Фігура, обмежена лемніскатою (рис.6.9), симетрична відносно горизонтальної і вертикальної прямих, проведених через полюс; тому досить обчислити площу S₁ четвертої її частини. Цій площі відповідає центральний кут [0, ]. Згідно з формулою (6.6)

Рисунок 6.9

2.Обчислення довжин дуг.

Нехай маємо дугу АВ, що є графіком функції y=f(x), визначеної і неперервної на [a,b] (рис 6.10). Розіб’ємо її точками А=А₀,А₁,…,A_n =B на n частин. Спрямимо лінію між сусідніми точками А_і-1 і А_і , тобто замінимо її відрізком, який сполучає ці точки (рис.6.10б).

Знайдемо довжини відрізків l_i , а потім і периметр утвореної ламаної, вписаної в лінію з n ланок.

P_n=l₁ + l₂ +…+ l_n = l_i .

Рисунок 6.10 а)

Рисунок 6.10 б)

Означення. Довжиною дуги L називається периметр вписаної в цю лінію ламаної за умови, що кількість відрізків ламаної (ланок) n0, а довжина =max x_i0, тобто

(6.7)

Теорема. Якщо функція y=f(x), визначена на відрізку [a,b] , неперервна на ньому разом зі своєю похідною f’(x), то довжина L відповідної дуги існує і

L= (6.8)

Доведення. Маємо (див рис.6.10б)

l_i =

Застосовуючи теорему Лагранжа, знаходимо

, x_i^*[x_i-1,x_i]

Тоді ((l_i0)( x_i0))

L=

Отже, L= (6.9)

Цей інтеграл існує, оскільки похідна (x) непе-рервна на відрізку [a,b],а значить неперервною є і функція .

Наслідок1. Якщо дуга АВ задана параметрично x=x(t), y=y(t),t, x’(t), y’(t) неперервні, то

L= (6.10)

Наслідок 2. Якщо дуга задана в полярній системі координат =(),  і ^/ неперервна, то

L = (6.11)

Доведення. Вважатимемо, що дуги задано парамет-рично:

x=cos , y=sin. Тоді x^/2+y ^/2=( ^/cos -sin)²+

+( ^/sin +cos)² =²+ ^/2.

Застосовуючи формулу (6.10), дістанемо (6.11).

Приклади.

1. Обчислити довжину L дуги параболи y=x²,що знаходи-ться між точками О(0;0) і А(1;1)

Роз’язання. Ця дуга є графіком функції y=x² , х[0;1]. Тому згідно з формулою (6.9)

Рисунок 6.11

При обчисленні інтеграла використано формулу із таблиці основних інтегралів (лекція 1).

2. Обчислити довжину однієї арки циклоїди x=a(t-sint), y=a(1-cost) (рис 6.12)

Розв’язання. Маємо x ^/=a(1-cost), y ^/=asint. За формулою (6.10) дістаємо

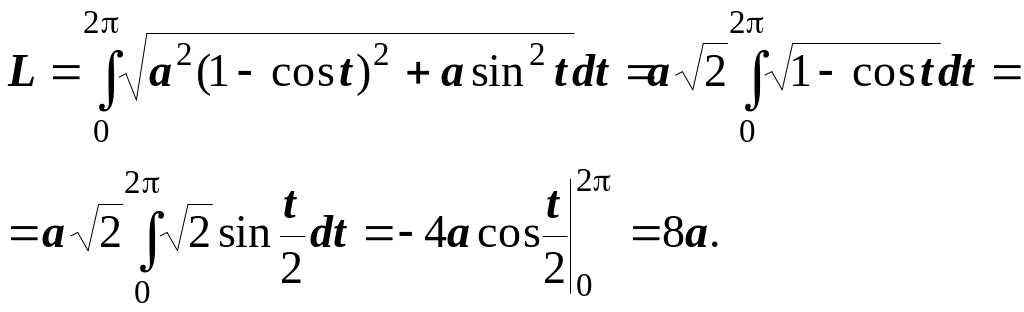
Рисунок 6.12

3. Обчислити довжину кардіоїди =a(1+cos).

Розв’язання. Побудуємо на координатній плёощині задану лінію (рис. 6.13). Оскільки крива симетрична відносно полярної осі, то досить обчислити довжину L₁ половини дуги. Згідно з формулою (6.11):

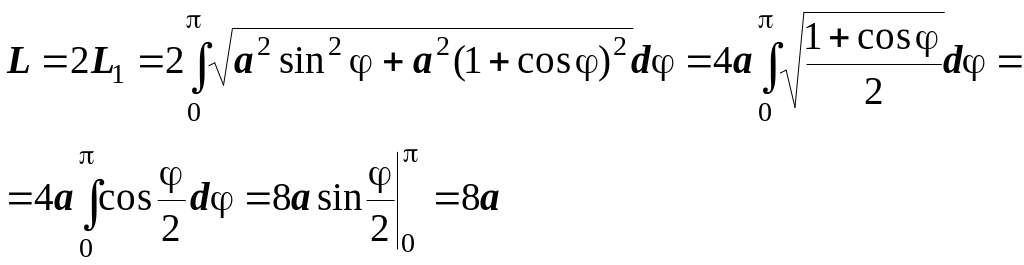
Рисунок 6.13