МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Івано-Франківський національний

технічний університет нафти і газу

Лялюк Д.Ф., Смоловик Л.Р.

ВИЩА МАТЕМАТИКА

ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ

ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

КОНСПЕКТ ЛЕКЦІЙ

МВ 02070855-1034-2003

Рекомендовано Вченою Радою Івано-Франківського

національного технічного університету нафти і газу

для студентів спеціальностей екологія та охорона навколишнього середовища, геологія нафти і газу, геофізика

Івано-Франківськ

2002р.

Лялюк Д.Ф., Смоловик Л.Р.

ВИЩА МАТЕМАТИКА

ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ

ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

КОНСПЕКТ ЛЕКЦІЙ

2002р.

ЗМІСТ

стор.

Лекція 1. Невизначений інтеграл...........................…….6

1. Первісна.......................................................................….6

2. Невизначений інтеграл.............................................……8

3. Властивості невизначеного інтеграла..................……...9

4. Таблиця невизначених інтегралів...........................…...10

5. Основні методи інтегрування.................................……12

Лекція2. Інтегрування дробово-

раціональних і деяких ірраціональ-

них функцій...........................................................…......17

2.1. Інтегрування елементарних дробів.......................……17

2.2. Інтегрування раціональних дробів........................……21

2.3. Інтегрування ірраціональних функцій.......... .......…....24

Лекція 3. Інтегрування тригономет-

ричних функцій. Застосування невиз-

начених інтегралів...................................................…..32

1. Інтегрування деяких тригономет-

ричних функцій........................................................…...32

2. Застосування невизначених інтег-

ралів .......................................................................…....40

Лекція 4. Визначений інтеграл...............................…...45

1. Приклади задач, які приводять

до поняття визначеного інтеграла.........................……45

2. Означення й тлумачення визначе-

ного інтеграла.......................................................…......48

3. Властивості визначеного інтеграла....................……...50

4. Обчислення визначеного інтеграла

за допомогою невизначеного..............................……...53

Лекція 5. Методи обчислення визна-

ченого інтеграла. Невластиві інтеграли..........……......57

1. Інтегрування заміною змінної ( метод

підстановки).....................................................…...........57

2. Інтегрування частинами...............................…….........59

3. Невластиві інтеграли першого роду.................……....62

4. Невластиві інтеграли другого роду..............…….......68

Лекція 6. Застосування визначеного

інтеграла...........................................................…..........73

1. Обчислення площ плоских фігур……...........................73

2. Обчислення довжин дуг......................................…......80

3. Обчислення об’ємів тіл..........................................…...84

4. Обчислення площ поверхонь обертання……………..91

Теоретичні ( екзаменаційні ) питання...................………...95

Перелік посилань............................................ ..........……..97

Лекція 1

Невизначений інтеграл

У математиці переважно для кожної дії над певними

об’єктами (числами, функціями, векторами та інш.) визна-

чається і обернена дія. Основною дією диференціального

числення є диференціювання – знаходження похідної для

заданої функції. Оберненою до дії диференціювання є дія інтегрування – відшукання такої функції, для якої дана

функція є похідною. Знаємо, наприклад, як за відомим за-

коном руху S = S(t) знайти швидкість: V = S’(t). Тоді обер-

нена дія – знайти закон руху за відомою швидкістю ( інтег-

рування ). Отже, якщо в процесі диференціювання функції розв’язується задача знаходження швидкості зміни функції,

то в процесі інтегрування функції знаходимо саму функцію

за відомою швидкістю зміни цієї функції.

1.1. Первісна

Якщо y = x² і = 2x, то можемо сказати, що функції x² відповідає інша функція 2x - ( її похідна ). І, навпаки, функ-

ція x² відповідає функції 2x. Функцію x² в цьому випадку називають первісною для функції 2х.

Взагалі, первісною називають функцію, відновлену за відомою її похідною або диференціалом.

Означення 1.1.Функція F(x) називається первісною для

функції f(x) на деякому інтервалі [a , b], якщо F^/(x) = f(x)

або, що те ж саме, dF(x) = f(x)dx  x є[a , b]. Означення не

вказує правило яким способом для функції f можна знайти

її первісну F. Воно лише дає змогу здійснювати перевірку кандидата на первісну.

Приклади.

1.Якщо

2.Якщо

3.Якщо

Якщо

і взагалі

Це є загальний вигляд первісної для f(x) = x⁴.

Теорема 1. (про загальний вигляд усіх первісних).

1. Якщо F(x) – первісна для f(x), то F(x) + C,CR, є також первісною для f(x).

2. Довільна первісна Ф(x) для f(x) має вигляд Ф(х) =

= F(x)+C,CR, де F(x) – одна з первісних для f(x).

Доведення. 1. Якщо F^/(x) = f(x), то ( F(x) + C )^/ = f(x).

2. Нехай Ф(х) і F(x) – первісні для f(x), тобто Ф^/(x) = F^/(x) = =f(x).Тоді (Ф(х) – F(x) )^/= 0.

Отже, Ф(х) – F(x) = C, тобто Ф(х) = F(x) + C.

Теорема 2. (про існування первісної ).

Будь-яка неперервна на [ a, b ] функція має на цьому ін-

тервалі первісну. Доведення (ширшого твердження) в л.4.

1.2. Невизначений інтеграл

Означення. Невизначеним інтегралом від деякої функції

f(x) називається множина всіх первісних функій, тобто

F(x) + C ; позначається

f(x)dx = F(x) + C (1.1)

де F^/(x) = f(x). Тут f(x) – підінтегральна функція, -

підінтегральний вираз, а x- змінна інтегрування.

Слово “інтеграл” походить від латинського “integer”, що означає відновлювати. Операція знаходження невизначеного

інтеграла функції і називається її інтегруванням.

Приклади. 1. x²dx = + C ;

2.  cosxdx = sinx + C ;

3. = lnx + C, ( x  0)

З геометричної точки зору первісна – це лінія y = F(x), а невизначений інтеграл – це сім’я ліній y = F(x) + C. (рис.1.1).

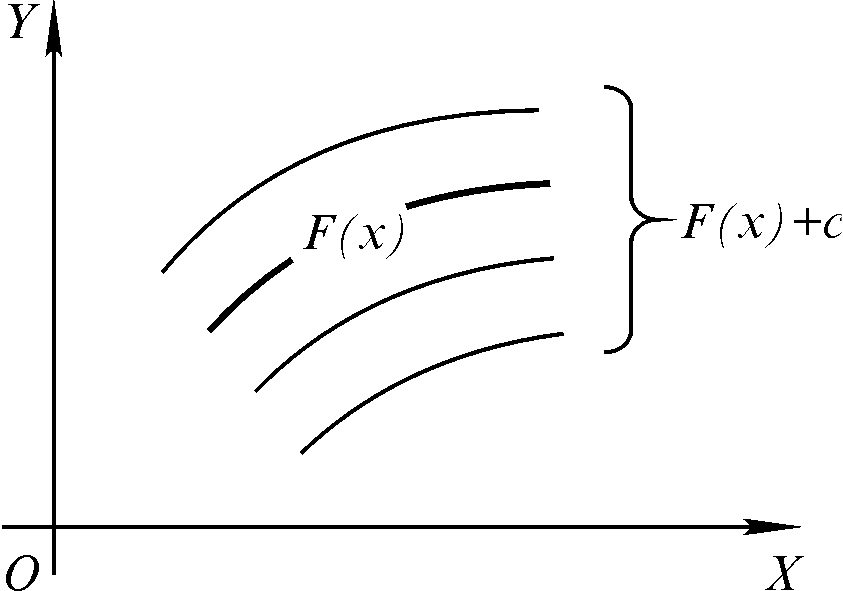
Рисунок 1.1