1. В зависимости от вида признаков, положенных в основу группировки:

А) атрибутивные — группировки, содержащие в качестве своей основы качественные признаки

Б) количественные — группировки, содержащие в своей основе количественные признаки;

2. По количеству признаков, используемых в процессе группировки:

А ) простая — группировка, в основу которой положен один признак;

Б) сложная — группировка, в основу которой положены несколько признаков;

В) многомерная — группировка, основанная на использовании одновременно целого комплекса взаимосвязанных признаков;

Г) комбинированные — группировки, при которых группы, сформулированные по одному признаку, подразделяются на подгруппы по другому признаку и т.д.;

Вопрос 2. Выполнение группировки по количественному признаку

В основание группировки могут быть положены как количественные, так и качественные признаки. После определения основания группировки, следует решить вопрос о количестве групп, на которые надо разбить изучаемую совокупность.

Число групп зависит от задач исследования и вида признака, положен­ного в основание группировки, численности совокупности, степени вариа­ции признака.

При построении группировки по качественному признаку групп, как правило, будет столько, сколько имеется градаций, видов, состояний у этого признака. Например, в случае проведения группировки населения по полу можно образовать только две группы: мужчины и женщины.

Если группировка проводится по количественному признаку, то необ­ходимо обратить особое внимание на число единиц исследуемого объекта . На количество выделяемых групп существенное влияние оказывает степень вариации группировочного признака: чем она больше, тем больше следует образовывать групп.

Для определения количества групп необходимо придерживаться двух важных условий построения группировок:

1. Выделенные группы должны отличаться качественной однородностью;

2. Количество единиц в каждой группе должно быть достаточно большим.

Оптимальное количество групп с равными интервалами можно определить по формуле американского ученого Стерджесса :

где N - число единиц совокупности.

Другой способ определения числа групп основан на применении пока­зателя среднего квадратического отклонения ( ). Если величина интерва­ла равна 0,5 , то совокупность разбивается на 12 групп, а когда величина интервала равна и , то совокупность делится соответственно на 9 и 6 групп.

Если совокупность разбивается на 12 групп, то интервалы групп стро­ятся следующим образом:

от до

от до

от до

от до

от до

от до

от до

от до

от до

от до

от до

от до

где - среднее значение признака по совокупности, которое определяется по формуле ,

- среднее квадратическое отклонение, согласно формуле :

.

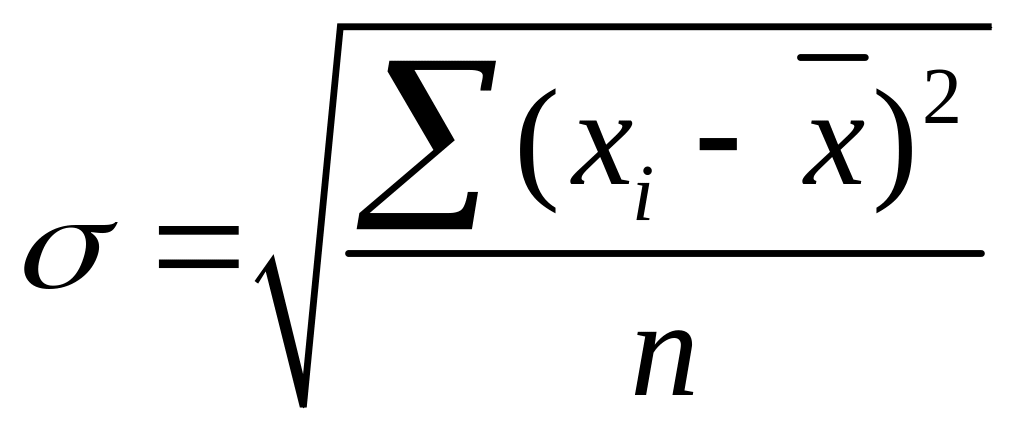где - i-e значение варьирующего признака;

Когда число групп равно 6, получаются следующие интервалы групп:

от до

от до

от до

от до

от до

от до

После определения количества групп следует определить интервалы груп­пировки.

Интервал – это количественное значение , отделяющее одну единицу (группу)от другой, т.е. интервал очерчивает количественные границы групп.

Каждый интервал имеет:

1.Нижняя граница интервала - это наименьшее значение признака в интервале;

2.Верхняя грани­ца - наибольшее значение признака в нем.

3.Величина интервала (ее еще часто называют интервальной разностью) представляет собой разность между верхней и нижней границами интервала.

Интервалы группировки в зависимости от их величины бывают:

1)рав­ные;

2) неравные:

а) прогрессивно возрастающие,

б) про­грессивно убывающие,

в) произвольные

г) специализированные.

Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами.

Величина равного интервала определяется по следующей формуле:

где R = - размах вариации;

- максимальное и минимальное значения признака в совокупности.

Полученную по формуле величину округляют..

Существуют следующие правила определения величины интервала:

1. Если величина интервала, представля­ет собой величину, имеющую один знак до запятой (например, 0,66; 1,372; 5,8), то полученные значения целесообразно округлить до десятых и их использовать в качестве шага интервала.

2.Когда рассчитанная величина интервала имеет две значащие цифры до запятой и несколько знаков после запятой, то это значение надо округлить до целого числа.

3. В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, эту величину необходимо округлить до ближайшего числа, кратного 100 или 50

Интервалы также могут быть:.

1. Открытые - это те интервалы, у которых указана только одна грани­ца: верхняя - у первого, нижняя - у последнего. Ширина открытого интервала принимается равной ширине смежного с ним интервала.

2.Закрытыми называются интервалы, у которых обозначены обе грани­цы.

Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:

в геометрической прогрессии:

где а - константа - число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным - при прогрессивно убывающих интервалах;

q - константа - положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих меньше 1.

3.Специализированными называются интервалы, применяющиеся для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.