5. Градуювальна та дисперсійна криві спектрографа
Після фотографування спектра джерела випромінювання проводять ототожнення його із спектром порівняння (довжини хвиль спектральних ліній у якому чітко визначені). Важливо, щоб спектр порівняння містив досить багато ліній в ділянці спектру, що нас цікавить.
За
допомогою вимірювального мікроскопа
проводять обмірювання спектрограми. В
результаті отримують з одного боку,
довжини хвиль
спектральних ліній, а з другого –
відповідні відліки міліметрової шкали
(відстань від певного нуль-пункта до
спектральних ліній). Отриману залежність
представляють графічно у вигляді
градуювальної кривої спектрографа
= f (
).
Взаємне
положення в спектрі ліній одного і того
ж хімічного елемента залежить від
застосовуваної для отримання спектра
апаратури. Так, якщо спектр отримано за
допомогою дифракційної гратки
(дифракційний спектр), то спектральні
лінії розміщуються одна від одної на
відстані
,
що пропорційно різниці довжин хвиль
.
Якщо ж спектр отримано на призмовому
інструменті (призмовий спектр) то
фіолетова ділянка спектра вийде дещо
розтягнутою, а червона — стиснутою;
відстань між спектральними лініями не
буде пропорційна різниці довжин хвиль.
Тому при обробці спектрограми необхідно
визначати масштаб різних ділянок
спектра, тобто інтервал довжин хвиль,
що вкладаються на одиницю довжини кожної
ділянки спектрограми. Такий масштаб
називають дисперсією ділянки спектрограми:
(7.26)
і вимірюється, як правило, в ангстремах на 1мм (А/мм) або нанометрах на 1 мм (нм/мм).
Очевидно, що дифракційний спектр має постійну дисперсію D впродовж всієї спектрограми, тимчасом як дисперсія призмового спектра поступово зменшується від фіолетової до червоної ділянки спектра (величина D зростає).
Зміну
дисперсії спектрограми звичайно подають
графічно у вигляді дисперсійної кривої.
Дисперсійна крива – це залежність
оберненої лінійної дисперсії від довжини
хвилі. Для її побудови потрібно для
кожної послідовно розміщеної пари
відомих спектральних ліній
і
розрахувати:
а) середню довжину хвилі:
(7.27);
б)
відношення
,
яке для близько розміщених ліній дорівнює
оберненій лінійній дисперсії.
Зауважимо,
що для розрахунку оберненої лінійної
дисперсії необхідно використовувати
спектральні лінії, по можливості, із
близькими значеннями
і
.
За допомогою побудованих графічних залежностей (градуювальна та дисперсійна криві) можна обчислювати довжини хвиль невідомих ліній у спектрі.
Найпростіше
(із невисокою точністю) це реалізується
на основі градуювальної кривої. Для
цього вимірюють відстань від нуль-пункту
до невідомої лінії на спектрограмі та
відкладають її числове значення на
координатній осі
,
із кінця відрізка відновлюють перпендикуляр
до перетину з градуювальною кривою. З
отриманої точки опускають перпендикуляр
на координатну вісь
,
за масштабом якої визначають довжину
хвилі невідомої спектральної лінії.
Суттєво
вищу точність забезпечують розрахунки
на основі дисперсійної кривої методом
лінійної інтерполяції довжин хвиль
невідомих ліній. Якщо спектральна лінія
з невідомою довжиною хвилі 
розміщується між лініями 
і 
,
відстань між якими 
,
а відстань між
і 
дорівнює 
,
то
(7.28)
Величина оберненої лінійної дисперсії може бути визначена за дисперсійною кривою, тому достатньо лише виміряти . Унаслідок нелінійності дисперсії метод дає задовільні результати тільки при невеликих відстанях між лініями.
Для
оцінки максимально можливого значення
використовують наступне очевидне
правило. Якщо на використовуваному
інтервалі
дисперсія змінюється на К%, то максимальна
похибка у визначенні довжини хвилі
лінії, що лежить усередині інтервалу,
не перевищує К% від нього.
Таким
чином, якщо
10
нм, а дисперсія змінюється на 2%, то
максимальна похибка у визначенні довжини
хвилі складає 0,2 нм.
Для призмових приладів в якості інтерполяційної формули використовують формулу Корню
або формулу Гартмана
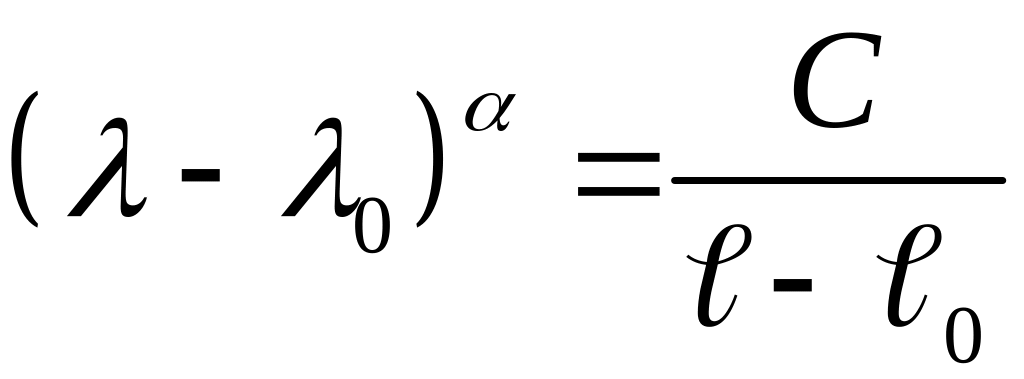
Величини
,
,
,
(
)
— постійні величини.
і
характеризують хід дисперсії,
визначається положенням пластинки на
вимірювальному столику,
залежить від точності вимірювання та
довжини вимірюваної ділянки спектру.
Якщо довжина вимірюваної ділянки спектра не перевищує 400 формула Корню забезпечує достатню точність розрахунків. В іншому випадку необхідно поділити спектр на декілька ділянок або використати формулу Гартмана.
Щоб
визначити константи формули Корню для
даної спектрограми необхідно визначити
положення на спектрограмі (
,
,
)
трьох ліній (
,
,
)
порівняння (всередині вимірюваної
ділянки та з боків).
Із трьох рівнянь
(7.29)
прийнявши
(тобто віднявши від
і
значення
),
легко знайти
Константу можна розрахувати із будь-якого з рівнянь (). Потім знайдену величину збільшують на .
Графічно
дисперсійна формула Корню в координатах
(
)
являє собою гіперболу, що асимптоматично
наближається до координатних осей —
так звану дисперсійну
криву.
Про диференціювавши формулу () маємо:
(7.30)
Отримана
формула дозволяє стверджувати, що в
призмових спектрах обернена лінійна
дисперсія
швидко зростає з довжиною хвилі.
Зауважимо, що в дифракційних спектрах дисперсія залишається практично постійною вздовж всієї пластинки.
Формула Гартмана, як і будь-яка емпірична інтерполяційна залежність, не дає можливості розрахувати точне значення , причому ступінь наближення різко погіршується із збільшенням інтервалу, охоплюваного формулою. Ступінь наближення також залежить від використовуваного інтервалу спектра та матеріалу призми. Наприклад, для кварцового спектрографа в інтервалі довжин хвиль 230-320 нм, похибка сягає 0,2 нм.
Зауважимо, що лінії порівняння слід підбирати так, щоб лінія з невідомою довжиною хвилі розміщувалася, по можливості, між ними.