3. Призмові спектрографи

Спектрограф (від спектр і грецького gropho – пишу) — спектральний прилад, в якому приймач випромінювання реєструє практично одночасно весь оптичний спектр розгорнутий у фокальній площині оптичної системи. Як приймач випромінювання використовується фотоемульсія або електронно-оптичні перетворювачі.

а) Фокальна поверхня спектрографа

Форма фокальної поверхні визначається властивостями диспергуючої системи та фокусуючої оптики, за умови використання призм та неахроматизованих об'єктивів, досить складна. Вона визначається впливом хроматичної аберації об'єктива камери та астигматизму призми, який рівний нулю лише для певної довжини хвилі.

Показник заломлення призми й об'єктива зростає із зменшенням довжини хвилі, відповідно, фокусна відстань об'єктива зменшується в напрямку до короткохвильової ділянки спектра. Таким чином, у кожній точці фокальна площина утворює деякий кут із променем, падаючим із центра об'єктива. Отже, для різних ділянок спектра цей кут різний. Але з певним наближенням можна обмежитися розглядом середнього кута нахилу до оптичної вісі лінзи, а фокальну поверхню вважати плоскою (рис. 6).

Наведемо орієнтовний розрахунок нахилу фокальної площини у кварцовому спектрографі із дзеркальним об'єктивом коліматора, неахроматизованим об'єктивом та 600  призмою, розміщеною в мінімумі відхилення (ИСП-22, ИСП-28, ИСП-30).

В

Рис. 2. До розрахунку нахилу фокальної поверхні до оптичної вісі спектрографа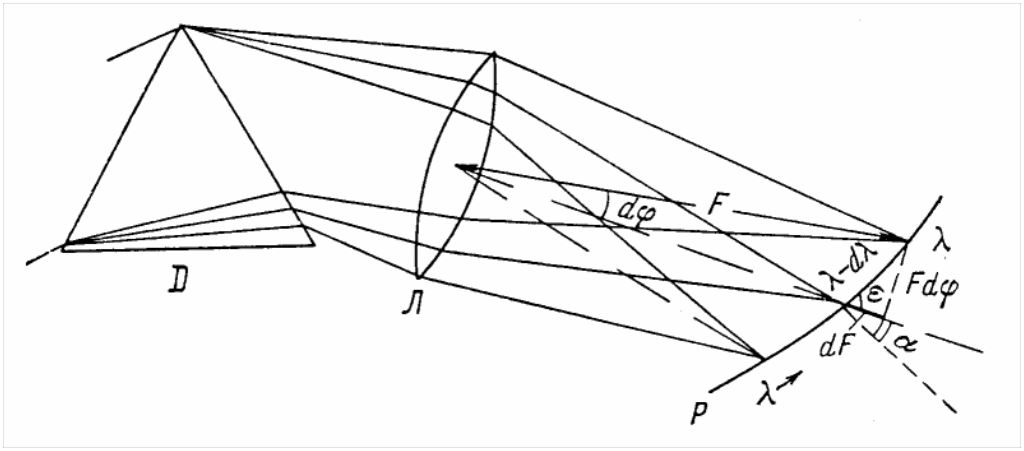

важаючи камерну лінзу тонкою, запишемо:

,

де n — показник заломлення матеріалу лінзи. Диференціюємо рівність по n :

(7.22)

З рис. 6 можна записати:

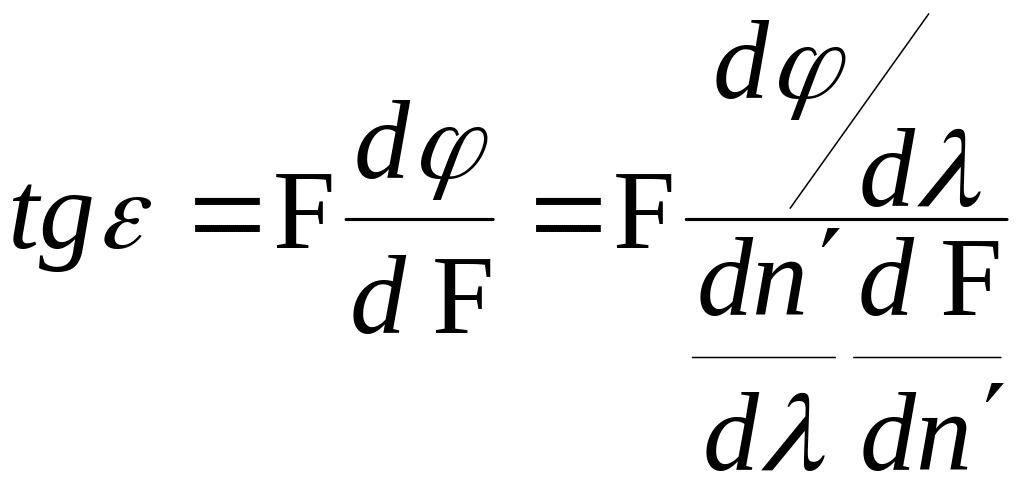
Використовуючи (7.22), отримаємо:

Підставивши значення кутової дисперсії призми в умовах мінімуму відхилення, маємо:

,

де n – показник заломлення призми.

Вважаючи , отримаємо:

(7.23)

Нахил касети, розрахований за формулою (7.23) для кварцового спектрографа (n = 1.6), складає 450.

При розрахунках не враховувалася зміна нахилу, викликана астигматизмом. Насправді для кварцового спектрографа ИСП-22 кут  420.

б) Лінійна дисперсія призмового спектрографа

Лінійна та кутова дисперсії призмового спектрографа пов'язані між собою. Дійсно, беручи за основу рис. 7, можна записати:

Тому

Тобто, з переходом до короткохвильової ділянки спектра зростає як лінійна, так і кутова дисперсія.

В икориставши формулу, що визначає кутову дисперсію призми (7.10), можна розрахувати лінійну дисперсію призмового спектрографа:

(7.24)

Для призмових приладів хід лінійної дисперсії у спектрі визначається як властивостями матеріалу призми, так і зміною фокусної відстані камери з довжиною хвилі. Перераховані фактори впливають взаємно протилежно, але вплив першого значно суттєвий.

Різкий спад лінійної дисперсії призмових приладів у довгохвильовій області спектра робить їх мало придатними для використання в червоній та інфрачервоній ділянках спектра.

в) Роздільна здатність призмового спектрографа

Визначення теоретичної роздільної здатності ґрунтується на критерії Релея, який формулюється на основі явища дифракції. Після певних перетворень можна отримати рівність, що виражає теоретичну роздільну здатність для призми:

(7.25),

де Т — основа тригранної призми, яка повністю заповнена світловим потоком.

З формули (7.25) випливає, що роздільна здатність призмового спектрографа прямо пропорційна розміру основи призми та дисперсії матеріалу і не залежить від заломлюючого кута.

Можна також довести, що для призми заданих розмірів найбільша роздільна здатність досягається в умовах мінімального відхилення (пучок світла повністю заповнює призму).