2. Спектральні призми

а) Заломлення в площині головного перетину

Спектральні призми (дисперсійні призми) — одна з груп оптичних призм; використовується для просторового розділення (розкладу в спектр) випромінювання оптичного діапазону, що розрізняється за довжинами хвиль. Розділення випромінювання на монохроматичні складові є результатом залежності кута відхилення променя, що пройшов через призму (рис. 2), від показника заломлення n, різного для променів різних довжин хвиль. Для речовин, прозорих у даній ділянці спектра, n зростає із збільшенням (зменшенням ), це відповідає розподілу кольорів у спектрі; така залежність n від називається нормальною дисперсією.

Для початку обмежимося проходженням променя світла в площині головного перетину призми – площина, яка перпендикулярна ребру призми та перетинає його посередині.

Н ехай на грань призми падає промінь під кутом до нормалі N1. Кут заломлення променя позначимо   , кут падіння на другу грань —  , кут виходу – . Кут   називають кутом відхилення.

Із рис. 2 запишемо:

,

Отримані рівності разом із законом заломлення дозволяють записати систему з чотирьох рівнянь, що пов'язують сім величин:

(7.1)

Використаємо систему рівнянь (7.1) для розрахунку умови мінімуму кута відхилення  . Для знаходження  продиференціюємо перше рівняння по  та прирівняємо похідну до нуля. 

(7.2)

Продиференціюємо наступні рівняння системи (7.1):

Таким чином:

(7.3)

Запишемо і через і у відповідно до двох останніх рівнянь системи (7.1):

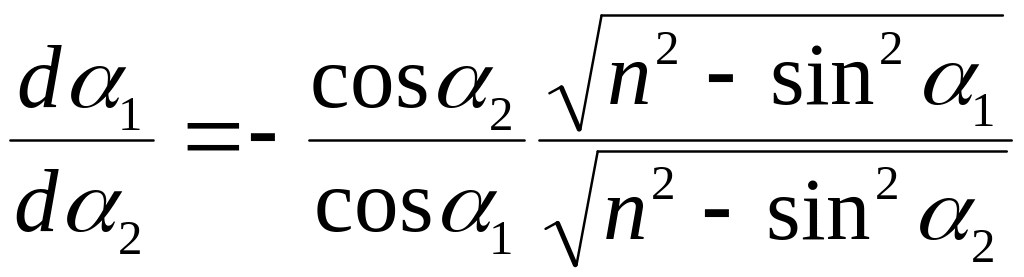(7.4)

З рівняння (7.2) і (7.4) отримаємо:

(7.5)

Рівняння (7.5) задовольняється за умови   . Це відповідає мінімуму кута   , бо при   виконується також умова . Падаючий промінь і промінь, що виходить із призми, виявляються симетричними щодо граней призми.

За умови мінімуму відхилення — кут падіння   , заломлюючий кут призми A, кут відхилення  і показник заломлення пов'язані між собою:

Якщо A = 600 , n = 1.6 то = 46о . Для переважної більшості спектральних приладів (з однією призмою) кут відхилення близький до розрахованого значення.

б) Дисперсія призми

Для розрахунку кутової дисперсії призми продиференціюємо по систему (7.1). При записі результату врахуємо, що ,

(7.7)

Після вилучення з рівнянь похідних і отримаємо:

(7.8)

або

(7.9)

За умови розміщення призми в мінімумі відхилення (рис. 3) , рівняння (7.7) запишемо у вигляді:

(7.10)

або

(7.11)

Таким чином, кутова дисперсія призми у мінімумі відхилення залежить від заломлюючого кута, показника заломлення та довжини хвилі.

Величина називається дисперсією матеріалу призми.

Залежність n = n ( ) можна описати емпіричною формулою Корню:

(7.12)

Продиференціювавши (7.12) та підставляючи в (7.10) маємо:

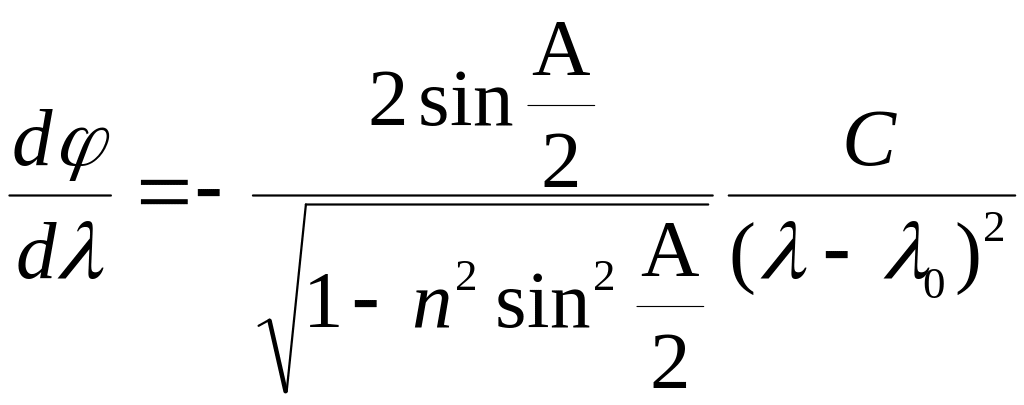(7.13)

Кутова дисперсія призми в мінімумі відхилення зменшується із зростанням довжини хвилі падаючого випромінювання.

Врахувавши, що і , де Т – основа призми, а – довжина її бокової грані, b – ширина падаючого пучка, (7.10) можна записати:

(7.14)

Якщо кут А=600 , то:

(7.15)

Отримана формула використовується для розрахунків у першому наближенні.

в) Кутове збільшення та астигматизм призми

Ми вважали, що на призму падає один промінь. Розглянемо більш близький до практики випадок падіння на поверхню призми вузького гомоцентричного пучка променів, що поширюються з точки S (рис 4).

Величина

(7.16)

називається кутовим збільшенням призми. Кут дорівнює зміні кута падіння ( ) для крайніх променів пучка, а кут   — зміні кута виходу променів ( ) із призми. Вважаючи кути та малими, замінимо різниці диференціюванням.

Таким чином, і відповідно з (7.3) отримаємо:

(7.17)

Якщо призма розміщена в мінімумі відхилення, то , і тоді .

На практиці на призму падає широкий пучок променів, не обов'язково паралельних площині головного перетину призми.

Досліджуючи заломлення пучка світла призмою у площині перпендикулярній головному її перетину, легко зрозуміти, що призма за таких умов діє як плоскопаралельна пластинка, не змінюючи напряму поширення променя.

Дійсно, як видно з рис. 4, при проходженні гомоцентричного пучка світла через призму він перетворюється таким чином, що вершина пучка наближається до призми або в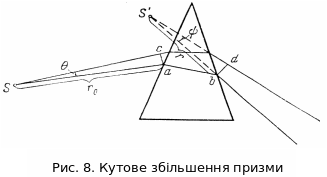 іддаляється від неї (відповідно до знака  ).

При цьому:

і

Враховуючи, що  , отримаємо:

Нехтуючи товщиною призми, можна розрахувати наближення пучка:

(7.18)

Зміна відстані від вершини пучка до призми виникає лише в площині головного перетину.

Т аким чином, вузький гомоцентричний пучок променів після проходження через призму стає астигматичним. Якщо розмістити за призмою об'єктив, то він фокусуватиме зображення точки S у площині Р як відрізок прямої, перпендикулярної заломлюючому ребру призми, а в площині Q — як відрізок, паралельний ребру. Відстань між цими площинами а можна розрахувати, знаючи величину r, фокусну відстань та положення лінзи L (рис. 5).

Позначимо фокусну відстань об’єктива через F, відстань від точки S до об’єктива через r і від об’єктива до зображення — а, тоді маємо:

Диференціюючи рівність, отримаємо:

За умови, що r  r0  a, тоді a  F і

(7.19)

Зображення точки щілини розтягується в напрямі, перпендикулярному дисперсії, на відстань

(7.20),

де D — діаметр об'єктива. Тоді можна записати:

(21)

З рівності (18) видно, що астигматизм призми рівний нулю, якщо   = 1, тобто за умови найменшого відхилення. Астигматизм, відповідно (7.18), також дорівнює нулю, якщо  (умова, що на призму потрапляє пучок паралельних променів). У цьому випадку всі промені пучка падають на призму й виходять із неї під однаковими кутами і, відповідно, зображення світної точки також буде точкою.

Із викладеного випливає необхідність у комплектації спектральних приладів коліматором.