3. Метод Гартмана

Метод Гартмана (1904) полягає у вивченні проходження різних ділянок (зон) об'єктива симетричними парами променів, що належать до осьового пучка. Метод дозволяє визначити кількісні характеристики аберацій об'єктива та зробити висновок щодо його якості.

Для дослідження об'єктива методом Гартмана використовується спеціальна діафрагма ― діафрагма Гартмана (рис. 17), що має певну кількість отворів у декількох кільцевих зонах, утворюючи в кожній зоні центральносиметричні пари отворів. При цьому отвори розташовані вздовж чотирьох діаметрів діафрагми, кути між якими становлять 45⁰ . Отже, відстані між усіма симетричними парами отворів у к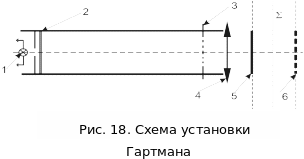 ожній зоні однакові. Один з отворів діафрагми є непарним для орієнтування при вимірюваннях.

Схема лабораторної установки зображена на рис. 18. Точкове джерело світла (1), розташоване на головній оптичній вісі об'єктива, фотографується через діафрагму Гартмана (3) із використанням різних світофільтрів (2), причому фотопластинка розташовується спочатку перед фокальною площиною (5) об'єктива (4) , а потім за нею (6).

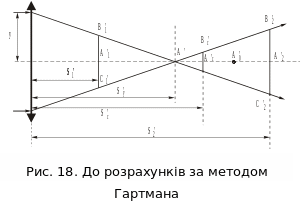
Нехай ми отримали передфокальний та зафокальний знімки штучної зірки через діафрагму Гартмана. На рис. 18 зображено хід двох симетричних відносно головної оптичної вісі світлових променів, тобто променів, що належать певній зоні. Будемо вважати об'єктив тонкою лінзою. Нехай А₀^' — фокус параксіальних променів (фокусна відстань лінзи дорівнює F ), А_c^' — центр мінімального кружка розсіяння, зумовленого сферичною аберацією, а А_c^' B_c^' = _C — його радіус. Точки А₁^' і А₂^' є центрами передфокального і зафокального знімків, B₁^'C₁^' = L₁ і B₂^'C₂^' = L₂  відстані між зображенням обраних променів на передфокальному і зафокальному знімках. і — відстані від об'єктива до передфокального та зафокального положень фотопластинки, — відстань до точки перетину даної пари променів, — відстань до найменшого кружечка розсіювання, y — радіус зони.

В изначимо спочатку . З подібності трикутників A^' B₁^'C₁^' і A^' B₂^'C₂^'маємо:

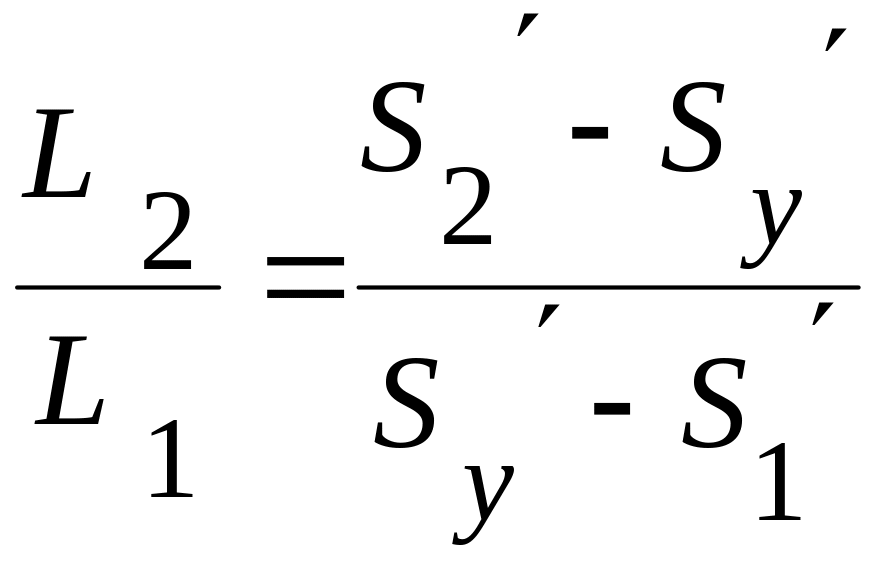
Тоді

Якщо до останньої рівності додати й відняти , то після приведення подібних, отримаємо:

(5.16)

Відповідно до (5.16) (де величини й наперед задані, а і вимірюються) розрахуємо відстані для всіх пар променів, що проходять через отвори діафрагми Гартмана. В ідеальному випадку для кожної зони діафрагми значення мають бути однаковими, але внаслідок похибок вимірювання та обрахунків вони дещо відрізняються.

Розрахуємо положення середніх фокусів зон як середнє арифметичне:

,

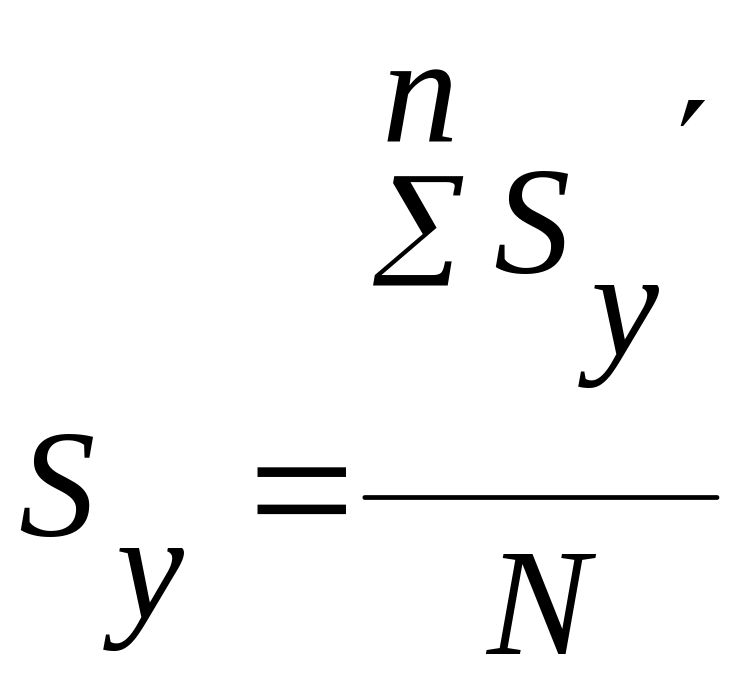де N — кількість значень у даній зоні (кількість пар променів у ній). Положення фокуса для всього об'єктива знайдемо як середнє зважене:

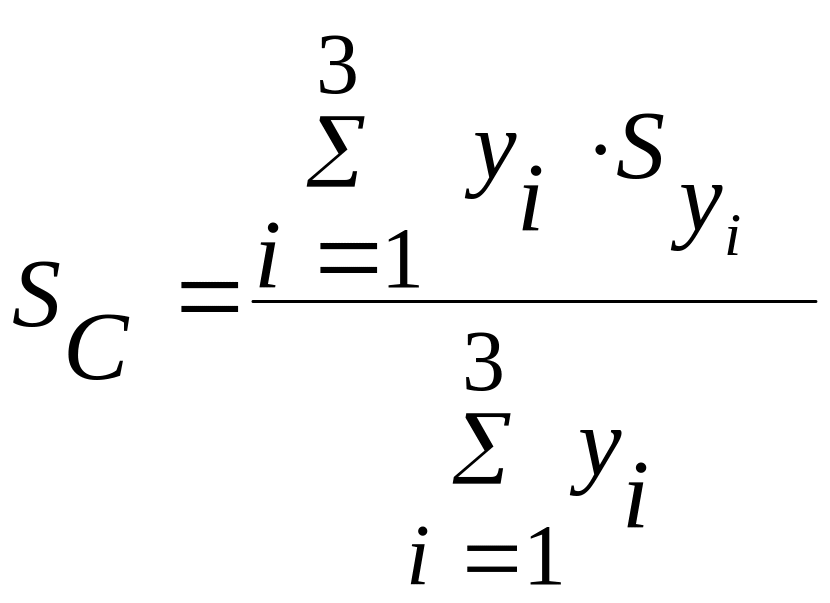(5.17)

де — радіус відповідної зони діафрагми, а — середній фокус цієї зони. Тепер можна визначити поздовжні сферичні аберації для кожної зони:

Зрозуміло, що для параксіальних променів маємо > 0, для червоних променів (за умови, що об'єктив не апланат) — < 0. Для апланата —

Поперечну сферичну аберацію даної зони об'єктива, тобто діаметр кружечка розсіювання, легко знайти з пропорції:

Знехтувавши , оцінимо верхню межу

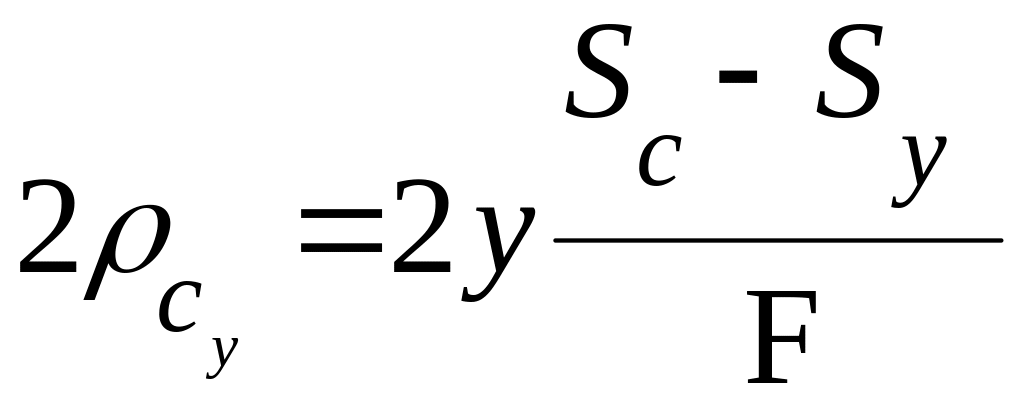(5.18)

Діаметр мінімального кружечка розсіювання визначається як середнє зважене за площинами зон від поперечних аберацій зон:

(5.19),

де F — задня фокусна відстань об'єктива.

Технічна константа об'єктива або стала Гартмана Т визначається, як діаметр мінімального кружечка розсіювання, виражений у стотисячних частках фокусної відстані:

(5.20)

Стала Гартмана дозволяє зробити висновок щодо якості об’єктива, якщо Т < 0,5 — об'єктив вважається першокласним, 0,5 < T 1,5 — добрим, 1,6 < T   2,5 — задовільним.

З'ясуємо фізичний зміст сталої Гартмана. Кутовий радіус мінімального кружечка розсіювання, зумовленого сферичною аберацією, у радіанній мірі дорівнює:

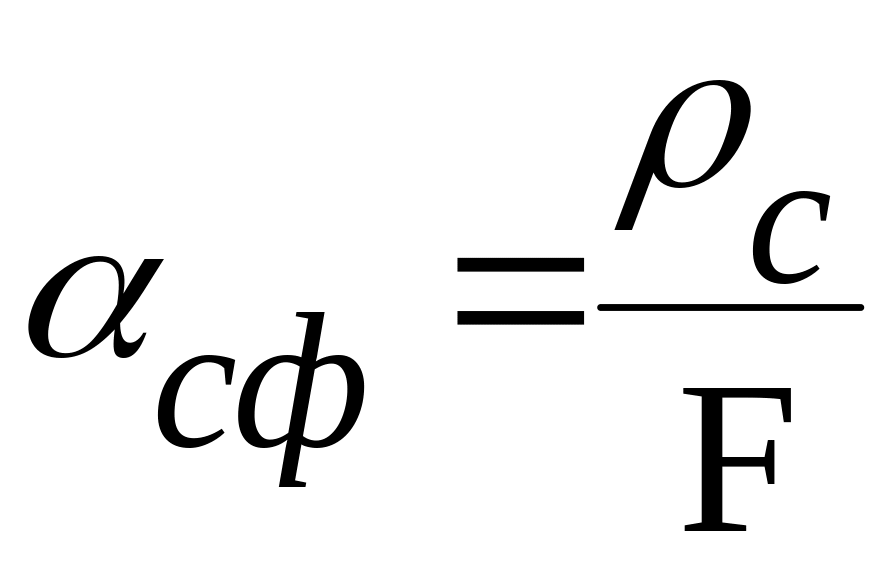(5.21),

а кутовий радіус дифракційного кружечка:

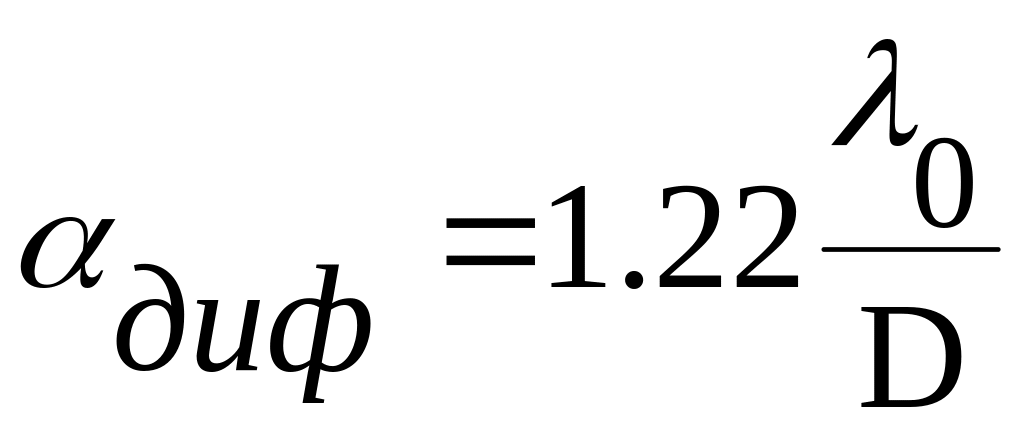(5.22),

де — ефективна довжина хвилі для фотооб'єктива (430 нм), D — діаметр вхідної зіниці. Визначивши і D у міліметрах, знайдемо відношення радіусів кружечків:

(5.23)

Тоді (5.20) можна записати:

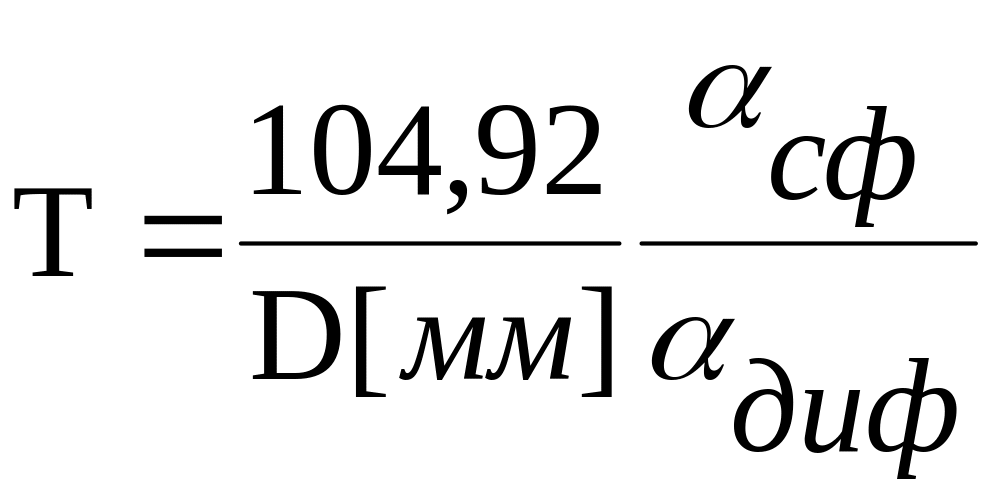(5.24)

Отже, технічна константа об'єктива пропорційна відношенню радіуса кружечка розсіювання, зумовленого сферичною аберацією, до радіуса дифракційного кружечка.