2. Зоряні величини та показник кольору

Блиск будь-якої зірки можна характеризувати декількома зоряними величинами, відповідно до способу їх реєстрації – візуальною m _v , фотографічною m _pg , фотовізуальною m_pv , фотоелектричною m_ph, болометричною m_b тощо. Усі шкали зоряних величин відносні й дають змогу лише порівнювати між собою блиск зірок у різних діапазонах довжин хвиль. Так, якщо блиск зорі визначається безпосередньо оком спостерігача (застосовуючи візуальний фотометр або без нього), то блиск зорі характеризується візуальною зоряною величиною m_v .

Фотографічна зоряна величина m _pg  визначається фотометруванням зображення зірок на фотопластинці, чутливій до синіх та ультрафіолетових променів (несенсибілізована фотоемульсія).

Фотовізуальна зоряна величина m_pv визначається шляхом фотометрування зображення зорі на ортохроматичній (очутливленій до жовто-зеленої ділянки спектра) фотопластинці, отриманого фотографуванням крізь жовтий світлофільтр. Візуальна та фотовізуальна зоряні величини зірки майже збігаються.

Різниця між фотографічною та візуальною зоряними величинами називається показником кольору (колор-індекс) CI:

CI= m _g - m _v

Прийнято, що зоряні величини зірок спектрального класу AOV в усіх системах зоряних величин однакові, тобто показник кольору рівний нулю. Для біло-голубих зірок спектрального класу O і B показник кольору є величиною від’ємною, а для зірок пізніх спектральних класів – додатною. Для Сонця CI  +0,6^m. Таким чином, можна зробити висновок, що показник кольору характеризує розподіл енергії у спектрі зірки і, відповідно, температуру її поверхневих шарів.

3. Методи абсолютної фотографічної фотометрії

В абсолютній фотографічній фотометрії шкала зоряних величин має будуватися незалежним (абсолютним) способом. Тобто, характеристична або градуювальна криві будуються за результатами спеціального допоміжного експерименту. Це можна досягнути двома шляхами. По-перше, стандартизацією фотопластинки виключно лабораторним шляхом (застосовується штучне джерело світла, яскравість якого змінюється у відомому відношенні за допомогою нейтрального фотометричного клину або експонуванням у трубчастому фотометрі). Слід зазначити, що для фокальних зображень точкових об'єктів викладений спосіб лабораторної стандартизації є неприйнятним.

По-друге, можна побудувати градуювальну криву за знімком ділянки зоряного неба, якщо на одній фотопластинці (або пластинках з однієї пачки) зробити два знімки, яскравість зірок на одному з яких послаблено на певний ступінь. При цьому експозиція має бути однаковою, а засоби послаблення світла не повинні змінювати спектральний склад випромінювання.

Розглянемо детальніше метод абсолютної фотографічної фотометрії, при якому зв'язок між блиском (зоряною величиною) спостережуваного об'єкта і фотографічним ефектом отримується за допомогою двох знімків ділянки зоряного неба, виконаних на одній фотопластинці.

Нехай маємо на фотопластинці фокальні зображення зірок певної ділянки зоряного неба і поряд зображення тих же самих зірок, але за умови послаблення світлового потоку від них на певну відому величину m. У результаті  вимірювань за допомогою мікрофотометра отримуємо набір числових значень густини почорніння зображень A, В, С, D — для першого знімка та, відповідні, а, b, с, d — для другого. Різниця A-а, В-b, С-с,... не буде постійною внаслідок похибок вимірювань і неоднорідності фотоемульсії.

Запишемо різницю у вигляді емпіричної функції півсум:

, , , …. (3.1)

Величина S, що дорівнює : 

, ,  , ,…. (3.2),

визначає ціну поділки вимірювальної шкали (мікрофотометра); ця величина є функцією членів послідовності (3.1).

П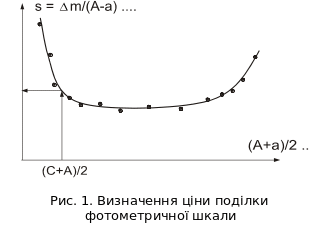 обудуємо графічну залежність між відповідними членами послідовності (3.1) та (3.2), провівши через отримані точки плавну криву (рис. 1)

Будемо вважати, що зоряна величина однієї із зірок дорівнює 0 ^m,00 (нехай це буде зірка А). Щоб знайти зоряну величину спостережуваної зірки С, слід за графіком (рис. 1), розрахувавши аргумент , визначити ціну поділки в зоряних величинах S. Тоді різниця зоряних величин зірок С і А дорівнює:

m = s (C - A) (3.3),

оскільки m _a= 0^m00 , то

m _с = s (C - A) (3.4)

Отриманий результат можна уточнити за допомогою послабленого зображення, тобто за необхідно, використовуючи графік, визначити та m = s ' (c - a), тоді:

m _с' = s (c - a) (3.5)

Розглянемо докладніше методи послаблення випромінювання зірок у відомому відношенні.

а) Метод діафрагм

Досліджуване зоряне поле фотографується без обмежувальної діафрагми, потім на об'єктиві закріплюють діафрагму, яка закриває спочатку половину вхідного отвору, потім 3/4 і так далі. Кожного разу фотографують з однаковою експозицією і на одну фотопластинку (трохи її зміщуючи). Діафрагму виготовляють у вигляді сектора — для уникнення можливого впливу різниці в прозорості об'єктива. У викладеному вище методі побудови калібрувальної кривої досить двох знімків, лише для контролю прозорості атмосфери перший знімок повторюють у кінці експерименту.

Теоретична величина послаблення:

m = – 2,5 Lg =  0^m,75 при отворі 1/2 (3.6)

Недоліками методу діафрагм є значні втрати часу та можливі зміни прозорості атмосфери протягом фотографування. Контрольний знімок дозволяє враховувати тільки систематичні зміни прозорості, не враховуючи випадкові. Метод діафрагм застосовується виключно для фокальних знімків.

б) Метод призмового супутника

Попереду об'єктива астрографа розміщують невелику за розміром призму з малим заломлюючим кутом. Спектр, утворюваний такою призмою, настільки короткий, що майже не відрізняється від зображення зорі. Обертаючи призму навколо заломлюючого ребра, можна отримати зображення спектра поряд із зображенням зорі, що будується частиною об'єктива, не прикритого призмою.

Якщо призма округлої форми, діаметром b, із діаметром оправи c, а діаметр об'єктива астрографа D, то “супутник” слабший за зображення зорі на:

  m = 2,5 Lg ( D ² - c ² ) - Lg b ² (3.7)

в) Метод сітки

Сітка з дроту, розміщена попереду об'єктива астрографа, утворює послаблене зображення зорі, оточене дифракційними спектрами. Відношення інтенсивностей центрального зображення і зображення, отримуваного без сітки, можна розрахувати, якщо відома товщина дроту d та ширина вільного проміжку x, за формулою:

=

Відповідно, в зоряних величинах:

m = 10 Lg  (3.8)

Наявність у виразі постійної показує, що вимірювання x  та d  слід проводити з максимально можливою точністю.

Метод сітки може з успіхом застосовуватися як для фокальних знімків, так і для позафокальних.