Міністерство освіти і науки України

Львівський автомобільно-дорожній коледж

НУ «Львівська політехніка»

ІНДИВІДУАЛЬНА

САМОСТІЙНА РОБОТА № 7

Тема: Основні поняття планіметрії

Студента групи _________

_____________________________________

Прізвище, ім’я

Варіант ________

Завдання для самостійної роботи №7

Тема: Основні поняття планіметрії

Мета: Пригадати практичні навички визначення розв’язування планіметричних задач.

Контрольні запитання:

1. Паралелограм – це…

2. Ромб – це…

3. Трапеція – це…

4. Запишіть за якими формулами обчислюють площу паралелограма.

5. Запишіть за якими формулами обчислюють площу трикутника.

6. Запишіть за якою формулою обчислюють площу ромба.

7. Виразіть площу трикутника через радіус вписаного кола.

8. Запишіть за якими формулою обчислюють площу трапеції.

9. Сформулюйте Теорему Піфагора.

10. Сформулюйте Теорему косинусів.

11. Сформулюйте Теорему синусів.

12. Виразіть площу трикутника через радіус описаного кола.

13. Чому дорівнює радіус описаного кола правильного трикутника?

14. Чому дорівнює радіус вписаного кола правильного трикутника?

Література:

1. Бевз Г.П., Бевз В.Г Математика 10. Рівень стандарту. – К.: Генеза, 2011 р.

Додатки, стор.254–260.

Методичні вказівки до розв’язування завдань самостійної роботи.

П риклад 1. У рівнобедреному трикутнику медіана, проведена до основи, дорівнює 25 см. Обчисліть площу цього трикутника, якщо радіус вписаного в нього кола дорівнює 10 см.

Розв’язування:

Нехай у рівнобедреному трикутнику ABC (АС = СВ) медіана СМ = 25 см (яка є і бісектрисою, і висотою) та радіус вписаного кола ОМ = 10 см. Ці відрізки не є сторонами одного трикутника. Тому для розв’язання задачі виберемо який-небудь відрізок як невідомий. Позначимо невідомий відрізок якоюсь буквою, наприклад х. Необхідно, щоб вибраний відрізок разом із даними відрізками утворював зручні для розв’язування трикутники.

Нехай AM = х, де x > 0. Цей відрізок можна об’єднати в прямокутні трикутники і з медіаною СМ і з радіусом ОМ.

Із Δ AMC: .

Щоби скласти рівняння, скористаємось тим, що центр вписаного кола лежить у точці перетину бісектрис: АО — бісектриса кута ВАС. Тоді АО є також і бісектрисою Δ AMC. За властивістю бісектриси внутрішнього кута трикутника , тобто .

Підносячи обидві частини одержаного рівняння до квадрата та розв’язуючи останнє рівняння, отримуємо: x²=500. Звідси x= .

Тоді S_ΔABC= (см²).

Відповідь. см².

Приклад 2. 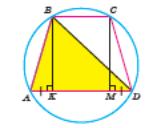У рівнобічній трапеції висота дорівнює 8 см, основи дорівнюють 21 см і 9 см. Знайдіть радіус описаного навколо трапеції кола.

Розв’язування:

Нехай у трапеції ABCD AB=CD, AD=21 см, ВС=9 см, ВК=8 см (ВК ⊥ AD ). Якщо коло проходить через чотири точки А, В, С, D, то воно також проходить через будь-які три із цих точок і тому збігається з колом, описаним навколо трикутника ABD. Знайдемо радіус кола, описаного навколо трикутника ABD.

Якщо СМ — друга висота даної рівнобічної трапеції, то, враховуючи рівність прямокутних трикутників АВК та DCM і те, що АD//ВС і ВСМК — прямокутник, одержуємо: AK=MD=(21–9)/2=6(см).

Тоді з ΔАВК: (см).

З прямокутного ΔBKD: (см).

Таким чином, радіус кола, описаного навколо трикутника ABD (а отже, і навколо трапеції ABCD), дорівнює (см).

Відповідь: 10,625 см.

П риклад 3. Периметр прямокутного трикутника дорівнює 24 см, а його площа — 24 см². Знайдіть радіус кола, описаного навколо трикутника.

Розв’язування:

Нехай у прямокутному трикутнику ABC: ∠C=90°, Р=24 см, S=24 см². Позначимо ВС=а, АС=b, АВ=с (а>0, b>0, с>0).

Записуючи дані периметр і площу та теорему Піфагора, одержуємо систему:

З першого рівняння a+b=24–с.

Тоді (a+b)²=(24–с)² або а²+2ab+b²=576–48с+с².

Підставляючи в цю рівність друге та третє рівняння одержуємо: с²+96=576–48с+с², звідки с=10 см. Оскільки радіус описаного кола прямокутного три кутника дорівнює половині гіпотенузи, тоді R=5 см.

Відповідь: 5 см.