2. Распределения вероятностей случайных величин

1.1. Теоретические сведения

Случайной величиной называется такая переменная величина, которая в результате опыта может принимать то или иное заранее неизвестное значение. Различают два основных типа случайных величин: дискретные и непрерывные. Дискретная случайная величина X может принимать конечное х_i (i = 1, 2 ,…, n) или бесконечное счетное множество значений х_i (i = 1, 2, …, ∞). Возможные значения непрерывной случайной величины не могут быть перечислены и непрерывно заполняют некоторый промежуток или даже всю ось.

Наиболее полной статистической характеристикой случайной величины является закон распределения вероятностей. В случае дискретной случайной величины X под ним понимается соотношение, устанавливающее зависимость между возможными значениями х_i дискретной случайной величины и их вероятностями p_i=р(х_i).

Закон распределения дискретной случайной величины можно задать в различных формах: таблично (ряд распределения), графически (многоугольник распределения), аналитически (в виде формулы).

Характеристикой, одинаково пригодной как для дискретных, так и для непрерывных случайных величин, является функция распределения W(x), определяющая вероятность P того, что случайная величина X не превысит некоторое число х:

.

Функцию распределения W(x) называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения обладает следующими свойствами:

1)

2) ; т.е. W(x) – функция неубывающая.

3)

Наряду с функцией распределения случайную величину часто характеризуют плотностью вероятности , которая определяется как производная функции распределения:

Плотность вероятности обладает следующими свойствами.

1) w(x) ≥ 0, т.е. плотность вероятности неотрицательна.

2) ;

3) - условие нормировки.

Плотность вероятности для дискретной случайной величины можно выразить через δ(x) - дельта-функцию (функцию Дирака):

.

Здесь x_i – возможные значения случайной величины X;

p_i – вероятности возможных значений x_i.

На рис. 2.1 показан вид функций распределения и плотностей вероятности для дискретных и непрерывных случайных величин.

Рис. 2.1

Систему из нескольких случайных величин можно рассматривать как точку в n-мерном пространстве со случайными координатами. Такую систему можно рассматривать как n-мерный случайный вектор или n-мерную случайную величину. При n=1 систему случайных величин можно рассматривать как обычную случайную величину и интерпретировать как точку со случайной координатой на прямой; при n=2 – как точку со случайными координатами на плоскости, а при n= 3 – в пространстве.

Наиболее полной характеристикой системы случайных величин является закон распределения вероятностей, который может быть задан функцией распределения или плотностью вероятности. В статистической теории радиосистем наиболее широкое распространение получили системы непрерывных случайных величин, которые обычно характеризуют не функцией распределения, а плотностью вероятности.

Функцией распределения W₂(x, у) системы двух случайных величин X, Y (иначе, совместной или двумерной функцией распределения) называется функция двух переменных х и y, характеризующая вероятность одновременного выполнения двух неравенств Х<х, Y<y

.

Геометрически функцию распределения W₂(x, у) можно интерпретировать как вероятность попадания случайной точки внутрь бесконечного левого нижнего квадранта с вершиной (х, у).

Если функция распределения F₂(x,y) непрерывна и обладает непрерывной смешанной производной второго порядка, то двумерная плотность вероятности w₂(x, у) определяется формулой

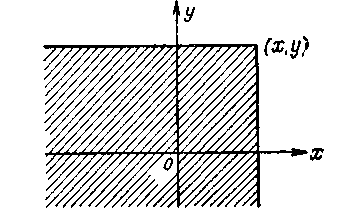
Рис. 2.2.

Функции W₂(x, у) и w₂(x, у) обладают следующими свойствами:

1) W₂(x,y) – неубывающая функция своих аргументов;

2)

3)

4)

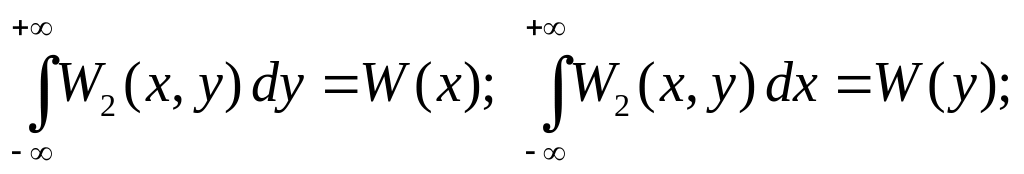
где W(x) и W(y) – одномерные функции распределения случайных величин X и Y ;

5) функция распределения W₂(x,у) связана с плотностью вероятности w₂(x, у) следующим образом:

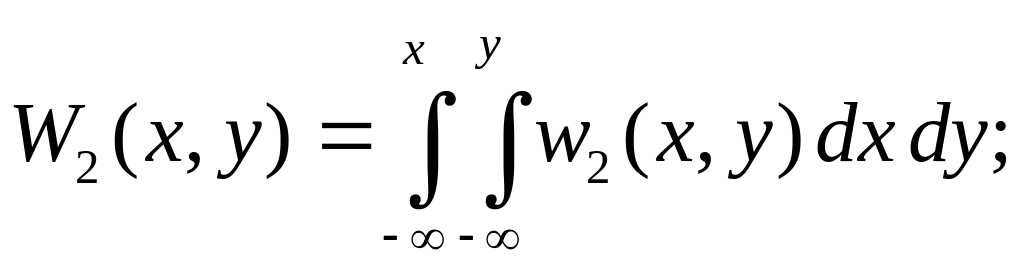
6) плотность вероятности w₂(x, у) функция положительно определенная и для нее выполняется условие нормировки:

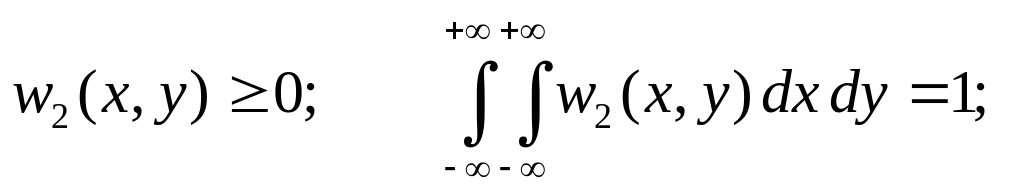
7) вероятность попадания случайной точки (X, Y) в прямоугольник со сторонами, параллельными осям координат, и с координатами вершин (x₁, y₁; х₂, у₁; x₁, y₂; х₂, у₂₎ определяется формулой

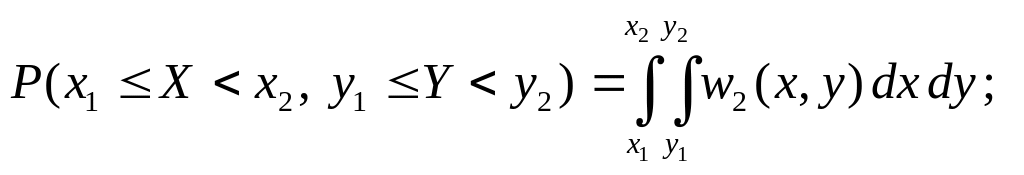
В теории измерений, теории стрельбы, теории обнаружения и оценок параметров сигналов и других приложениях широко используется нормальный (гауссов) закон распределения случайных величин, одномерная плотность вероятности которого имеет следующий вид:

, (2.1)

где m_x и σ_x - параметры распределения (среднее значение и среднеквадратическое отклонение случайной величины x).

Широкое распространение нормального закона в технических и научных приложениях объясняется тем, что в них часто встречаются задачи, в которых анализируемые случайные события и величины можно рассматривать как результат суммирования большого количества случайных факторов. В силу этого для таких событий и величин естественным образом выполняются условия центральной предельной теоремы теории вероятностей, согласно которой для достаточно широкого круга исходных условий распределение суммы большого числа случайных величин с увеличением числа суммируемых величин стремится к нормальному закону. На этой основе, в частности, получены рассмотренные в разделе 1 асимптотические приближения (1.17, 1.22).

Вероятность того, что распределенная по нормальному закону случайная величина X с параметрами m_x и σ_x находится в интервала [a,b) можно найти по формуле

, (2.2)

где 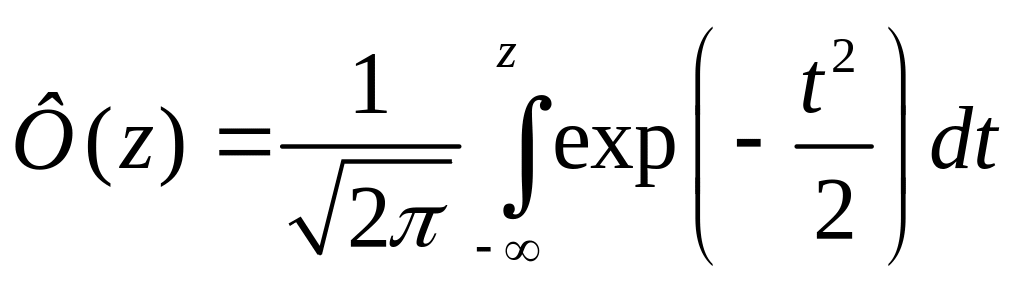- интеграл вероятностей, значения которого табулированы [ ].

В таблицах, обычно приведены значения Ф(z) при значениях аргумента z ≥ 0. Для нахождения интеграла при отрицательных значениях z можно воспользоваться очевидным соотношением , которое следует из симметрии нормального распределения относительно математического ожидания.

В приложениях статистической теории радиосистем при нахождении вероятностей превышения случайным сигналом с гауссовым распределением некоторого порогового уровня часто требуется вычислять интеграл

.

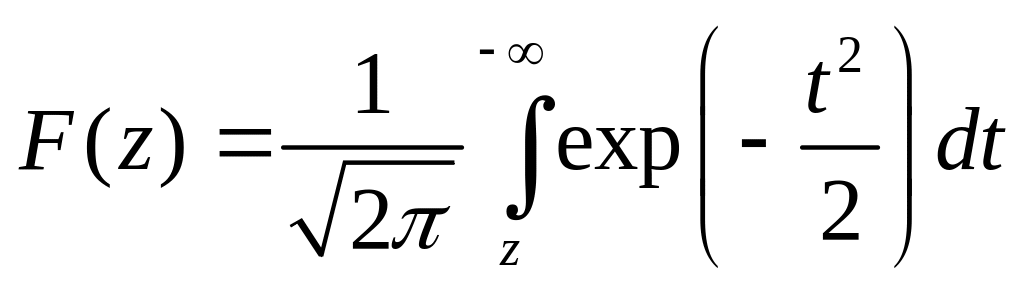Этот интеграл также выражается через Ф(z):

.

Среди других законов распределения, получивших широкое распространение в технических приложениях можно указать на распределения, тесно связанные с нормальным: распределения Рэлея и Рэлея-Райса (обобщенное распределение Рэлея) и кроме этого на распределение Пуассона и экспоненциальное распределение. Распределения Рэлея и Рэлея-Райса будут подробнее рассмотрены ниже (разделы 3, 4).

Распределение Пуассона

(2.2)

и экспоненциальное распределение

(2.3)

широко используют в вероятностных моделях явлений, описывающих случайные потоки независимых редких событий. Параметр λ представляет собой средний интервал между двумя соседними событиями потока, а величину λ^-1 называют интенсивностью потока.

Закон распределения системы двух случайных величин X, Y определяется распределением каждой из величин, входящих в систему, и зависимостью между ними. Степень зависимости случайных величин X и Y характеризуется условным законом распределения, под которым понимается закон распределения одной из случайных величин, найденный при условии, что другая случайная величина приняла определенное значение.

По теореме умножения вероятностей зависимых случайных величин имеем

(2.4)

где – условные плотности вероятностей. Для независимых случайных величин , а

Это соотношение является необходимым и достаточным условием независимости случайных величин.

Плотность вероятности w₂(x, у) для системы из двух нормальных случайных величин (X, Y) имеет вид

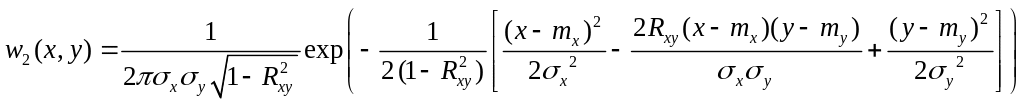(2.2)

где т_x, т_у — математические ожидания X и Y; σ_x σ_у — среднеквадратические отклонения; R_xy - коэффициент корреляции случайных величин X и Y.

Если R_xy = 0, т. е. случайные величины X и Y не коррелированны между собой, то плотность вероятности w₂(x, у) распадается на произведение двух одномерных плотностей вероятности

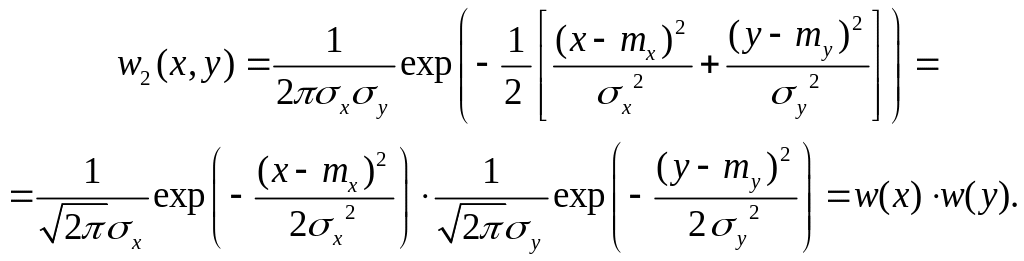
А это означает, что случайные величины X иY являются статистически независимыми. Следовательно, из коррелированности случайных величин с нормальным распределением следует их статистическая независимость.

Условные и безусловные плотности вероятностей связаны между собой следующим образом:

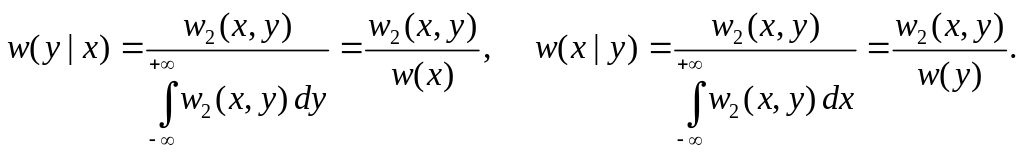(2.6)

Свойства условных плотностей вероятностей аналогичны свойствам безусловных плотностей вероятностей.

Формулы полной вероятности и Байеса через плотности вероятности выражаются следующим образом:

(2.7)

Приведенные выше выражения можно обобщить на n-мерные функции распределения W_n(x₁,x₂, ..., x_n) и плотности вероятности w_n(x₁,x₂, ..., x_n), которые описывают систему из n случайных величин (n-мерный случайный вектор) [1].

В ряде приложений наряду с распределением случайной величины X применяют характеристическую функцию (и), связанную с плотностью вероятности w(x) преобразованием Фурье:

(2.8)

где - мнимая единица.

К характеристической функции применимы все свойства преобразования Фурье. Одним из важных приложений характеристической функции в статистической теории радиосистем является возможность относительно просто находить распределение суммы нескольких случайных величин. Как известно, для нахождения плотности вероятности суммы нескольких случайных величин необходимо вычислить интеграл свертки. Это, обычно, достаточно сложная математическая задача, если ее решать «в лоб». Однако, если учесть, что Фурье-образ интеграла свертки равен произведению Фурье-образов свертываемых функций, то задачу нахождения плотности вероятности суммы нескольких случайных величин можно решить, перемножив характеристические функции суммируемых случайных величин и выполнив обратное преобразование Фурье от этого произведения. Этот путь решения задачи привлекателен тем, что для нахождения обратного преобразования Фурье можно воспользоваться обширными таблицами преобразований Фурье и Лапласа.

Другим приложением характеристической функции является возможность упростить нахождение числовых характеристик случайной величины: математического ожидания, дисперсии и т.д. (см. раздел.3).