47

Основы Статистической теории радоисистем

Пособие для решения задач

Часть 1

Теория вероятностей

Таганрог 2008

1. Основные теоремы теории вероятностей

1.1 Теоретические сведения

Основными понятиями теории вероятностей являются понятие события и понятие вероятности. Событие это явление, которое в результате некоторого действия может либо произойти, либо нет. Различают достоверные, невозможные и случайные события. [1, 2, 3]. Достоверные события обозначаются буквой U, невозможные – V, a случайные – буквами А, В, С, ... . Мерой случайности события является вероятность его появления P(A). Вероятность достоверного события принимается за единицу, а вероятность невозможного – за нуль:

P(U) = 1, P(V) = 0.

Таким образом, вероятность случайного события A изменяется в пределах от 0 до 1:

0<P(A)<1.

Наряду с одиночными событиями рассматривают группу (множество) событий. В группе событий помимо вероятности появления каждого из них необходимо характеризовать взаимную связь между событиями в группе. События в группе могут быть независимыми или зависимыми между собой. Если всякий раз, когда происходит событие А, происходит так же событие В, то говорят, что событие A влечет за собой событие и такое явление обозначают AB. Если AB и в то же время ВА, то говорят, что события А и В равносильны, и обозначают А = В. В этом случае P(A) = P(B).

Суммой (объединением) множества событий А,В,С,... называют такое событие, которое происходит тогда и только тогда, когда происходит по крайней мере одно («хотя бы одно») из этих событий. Сумма событий А, В, С, ... обозначается выражениями A + B + С + … или AUBUСU… . Если событие в группе обозначить А_k (k=1,2, … ,M) то сумма этих событий обозначается или .

Непосредственно из определения суммы событий вытекают следующие соотношения:

A+A=A; A+U=U; A+V=А,

а также переместительный и распределительный (коммутативный) законы:

А+В=В+А; (А+В)+С=А+(В+С).

Произведением (или совмещением, или пересечением) событий А,В,С... называется событие, происходящее тогда и только тогда, когда все события происходят вместе («одновременно»). Произведение событий обозначают ABC… или или .

Для произведения событий очевидны следующие соотношения:

АA = A; AV = V; AU = A,

а также перемести тельный и распределительный (коммутативный) законы:

АВ = ВА; (АВ)С= А(ВС).

Для операций умножения и сложения событий, применяемых совместно, справедлив обычный распределительный (дистрибутивный) закон

(A+В)С=АС+ВС

и так называемый «второй распределительный закон» [3]

АВ+С=(А+С)(В+С).

События А,В,С,... образуют полную группу событий, если в результате действия непременно должно появиться хотя бы одно из них. Другими словами, сумма событий, образующих полную группу, является достоверным событием, т. е.

А+В+С+...=U.

События а и В называют несовместными (или несовместимыми), если их совместное появление невозможно, т. е. если

АВ=V.

Два несовместных события, образующих полную группу, называются противоположными (или дополнительными) событиями. Событие, противоположное событию А, обозначается .

Для противоположных событий справедливы формулы:

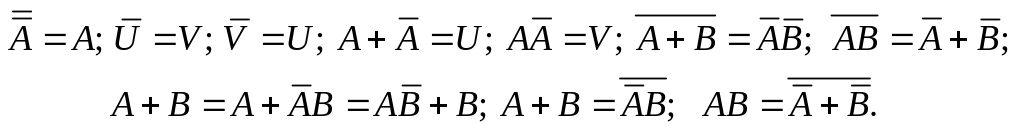(1.1)

Нетрудно заметить, что для противоположных событий эти формулы аналогичны соответствующим формулам булевской алгебры (алгебры логики). Противоположному событию соответствует операция логического отрицания (инверсии), сумме событий – логическая операция “ИЛИ” (дизъюнкция), произведению – логическая операция “И” (конъюнкция).

Если явление имеет N равновозможных исходов, которые несовместны и составляют полную группу (такую ситуацию называют схемой случаев), то вероятность Р(А) наступления события А определяется формулой

,

где п – число исходов, которые приводят к наступлению события А.

Таким образом, для нахождения вероятности Р(А) в рассматриваемом случае необходимо найти числа N и n и вычислить их отношение. При решении задач такого типа общие способы для нахождения чисел N и п неизвестны. Часто для вычисления указанных чисел полезно использовать методы комбинаторной алгебры: размещения, перестановки, сочетания.

Размещениями из N элементов по m называют такие их комбинации, которые различаются друг от друга или самими элементами или их порядком. Например, два элемента из трех a, b, c можно разместить следующими способами: ab, ac, bc, ba, ca, cb. Число возможных размещений определяется формулой

. (1.2)

Перестановками из N элементов называют такие их комбинации, которые различаются друг от друга только порядком входящих в них элементов. Например, возможные перестановки из трех элементов a, b, c: abc, acb, bac, bca, cab, cba. Число возможных перестановок определяется формулой

. (1.3)

Если среди элементов a, b, c … имеются одинаковые (a повторяется α раз, b – β раз, с – γ раз и т.д.), то

. (1.4)

Сочетаниями из N элементов по m называют такие их комбинации, которые различаются друг от друга только самими элементами, а порядок элементов во внимание не принимается. Например, два элемента из трех a, b, c можно сочетать следующими способами: ab, ac, bc. Число возможных сочетаний определяется формулой

. (1.5)

Для вычисления N! и m! при больших значениях N и m удобно использовать приближенную формулу Стирлинга

, (1.6)

которая дает приемлемую точность и при небольших значениях k [3]. Например, при k >1 ее относительная погрешность не превышает 10%, а при k > 10 – 1%, а при k > 100 – 0,1%.

Понятие равновозможности событий иногда применяют к опытам с бесконечным числом исходов, когда числа N и п в формуле (1) определить невозможно: проще вычислить саму вероятность события, а не порознь числа п и N.

В таких случаях пользуются геометрическими интерпретациями возможных исходов исследуемого явления, и вероятность наступления события A определяют по формуле

, (1.7)

где G – геометрическая мера (длина отрезка, площадь фигуры, объем тела и т. д.) всей области возможных исходов исследуемого явления; g – геометрическая мера части той области G, попадание в которую благоприятствует событию А.

Нахождение вероятностей сложных событий (например, появления той или иной цепочки событий, суммы или произведения событий) базируется на использовании основных теорем теории вероятностей (теоремы сложения и умножения вероятностей и их следствий).

Согласно теореме сложения вероятностей вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:

Р(А+В)=Р(А)+Р(В)-Р(AВ). (1.8)

Если события A и В несовместны, то

Р(А+В)=Р(A)+Р(В).

Эти формулы обобщаются на сумму любого числа событий.

Сумма вероятностей несовместных событий, составляющих полную группу, равна единице:

.

Сумма вероятностей двух противоположных событий равна единице:

По теореме умножения вероятностей вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:

Р(АВ) = Р(А)Р(В|А) = Р(В)Р(А|В), (1.9)

где Р(А|В) – условная вероятность события A, т. е. вероятность появления события А при условии, что произошло событие В.

Если событие А статистически не зависит от события В, то Р(А |В) = Р(А). В этом случае события А и В называют независимыми. Для независимых событий A и В

Р(АВ) = Р(А)Р(В). (1.10)

Последние две формулы можно обобщить на N событий A₁ A₂, ..., A_N:

Теоремы сложения и умножения вероятностей совместного используются при решении многих практических задач. Одним из важных приложений этих теорем является оценка надежности систем.

Надежность системы (или ее элемента) оценивают по вероятности того, что система (элемент) в течение установленного времени будет работать без отказов.

При объединении нескольких элементов в систему они могут соединяться параллельно, последовательно, либо использоваться их смешанное соединение. При параллельном соединении отказ системы возможен только при одновременном отказе всех элементов, а при последовательном система отказ системы происходит при отказе любого элемента.

Вероятность безотказной работы системы при параллельном соединении k элементов и независимых отказах можно рассчитать по формуле

, (1.11)

где p_i – вероятность безотказной работы i-ro элемента. С ростом k произведение в последней формуле стремится к нулю, а P – к единице. Следовательно, с увеличением числа параллельно включенных элементов надежность системы возрастает.

Вероятность безотказной работы системы при последовательном соединении k элементов при независимых отказах вычисляется по формуле

. (1.12)

С увеличением числа последовательно включенных элементов надежность системы убывает.

Во многих ситуациях то или иное событие А может появиться лишь как случайное следствие одного из несовместных событий H_i, (i =1, 2, ... , N), которые входят в некоторую полную группу событий и называются гипотезами. В таких случаях безусловная вероятность Р(А) события А при известных вероятностях гипотез Р(Н_i) и условных вероятностях Р(А|H_i) определяется по формуле полной вероятности:

(1.13)

При этих же данных, т. е. известных вероятностях P(H_i) и Р(А|H_i), можно найти вероятностей гипотез H_i, если событие А уже произошло. Задачи подобного типа решаются с помощью теоремы гипотез (или формулы Байеса)

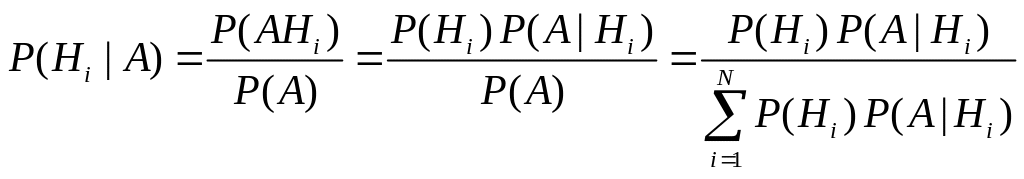. (1.14)

Вероятность P(H_i) называется априорной (или доопытной), а P(H_i|A) – апостериорной (послеопытной) или обратной вероятностью.

Формула Байеса лежит в основе ряда алгоритмов принятия решений в статистической теории радиосистем при обнаружении и оценке параметров сигналов (так называемые байесовские методы и алгоритмы).

В теории передачи сообщений, теории стрельбы, контроле качества продукции и т. д. одной из наиболее распространенных задач является нахождение вероятности появления некоторого количества событий в результате серии опытов, в каждом из которых наблюдаемое событие может произойти с некоторой вероятностью p_i. Проще всего такая задача решается, если опыты являются независимыми (т. е. вероятность появления события не зависит от того, какие исходы имели другие опыты) и однородными (т.е. вероятность появления события не изменяется от опыта к опыту). Способ решения подобных задач дает теорема о повторении опытов (теорема Я. Бернулли).

Вероятность Р_n(k) того, что при N независимых опытах (испытаниях) событие А появится ровно k раз, если при каждом опыте вероятность события А одинакова и равна р, определяется формулой Я. Бернулли

. (1.15)

При больших значениях N этой формулой пользоваться неудобно. В этом случае для расчета вероятности P_N(k) можно применять приближенные формулы, основанные на асимптотических приближениях.

Если N велико, р мало, а Nр = имеет конечное значение, то для расчета P_N(k) можно пользоваться приближением Пуассона

. (1.16)

Погрешность этого приближения можно оценить по формуле

.

Когда npq не слишком мало, то применяется гауссова аппроксимация распределения Бернулли (формула Муавра – Лапласа)

. (1.17)

Погрешность гауссовой аппроксимации при вычислении вероятности P_N(k) можно оценить по формуле

Вероятность Р_N(km) того, что наблюдаемое событие в серии из N независимых опытов произойдет не менее m раз, если в каждом из опытов оно происходит с вероятностью р, рассчитывается по формуле

. (1.18)

Вероятность Р_N (k1) появления события хотя бы один раз при N опытах равна

Р_N ( k 1)= (1- (1- p )^N). (1.19)

Вероятность Р_N (k  m) того, что при N независимых опытах рассматриваемое событие появится не более k раз, определяется выражением

. (1.20)

Вероятность Р_N (l k  m) того, что при N независимых опытах рассматриваемое событие появится не менее l и не более k раз можно рассчитать по формуле

. (1.21)

При больших значениях N, l и m этой вычисления по этой формуле становятся громоздкими. В этом случае можно использовать ее гауссово приближение

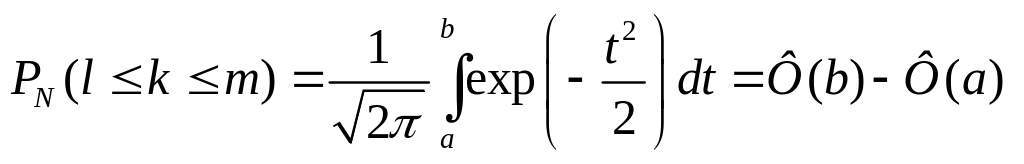, (1.22)

где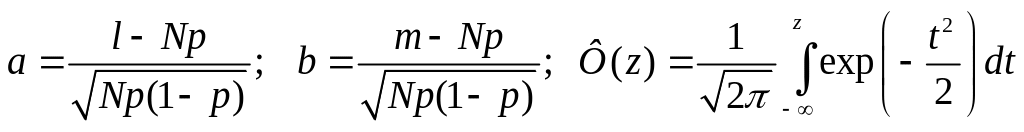

Количество опытов N, которые нужно выполнить для того, чтобы с вероятностью не меньшей Р₁ можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле

. (1.23)

Эта формула получается из очевидного соотношения . Логарифмируя это выражение по произвольному основанию, получим рассматриваемую формулу.

Наиболее вероятное число появлений события А в N независимых опытах k₀ определяется из неравенства

(N+1)p - 1 k₀ < (N+1)p. (1.24)

Если же число (N+1)p целое, то неравенство определяет два значения наиболее вероятного числа k₀ появлений события А в N независимых опытах.

Теорема Бернулли представляет частный случай теоремы о повторении опытов. Известен ряд ее обобщений. Для статистической теории радиосистем представляют интерес два из них. Одно заключается в том, что вероятность наблюдаемого события р при проведении серии опытов изменяется от опыта к опыту. Второе состоит в том, что каждый опыт может иметь не два, а большее число исходов. Формулы для расчета соответствующих вероятностей можно найти в работе [3].