Задание 4

Найти линию, у которой любая касательная пересекается с осью ординат в точке, одинаково удаленной от начала координат и от точки касания.

Решение

Произведем разбор условия задачи

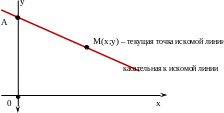
А – точка пересечения с осью ординат касательной, проведенной в произвольно выбранной точке (х,у) искомой линии.

По условию задачи |AM|=|AO| для любой точки M(x,y) искомой линии.

Требуется найти линию в виде её уравнения у = у(х) или F(х,у) = 0.

Составим математическую модель к данной задаче:

Искомую функцию у = у(х) нужно находить из условия |AM|=|AO| => надо составить уравнение касательной к линии и находить координаты её точки А.

Используем теоретическое уравнение касательной к линии y=y(x) в её фиксированной точке М(x₀,y₀):

В решаемой задаче уравнение касательной запишем в следующем ви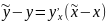де:

. , где

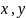( ) – координаты точки касания;

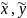( ) – текущая точка на касательной.

Для нахождения ординаты точки А нужно в уравнении касательной положить 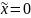и , в результате получим: .

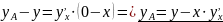Расстояние |AM| и |AO| найдем по известной формуле для расстояния между двумя точками на плоскости:

|AM|=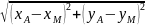 =>|АМ|= = ;

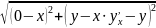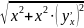|AO|= = ;

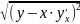|AM|=|AO| => |AM|²=|AO|² => .

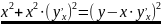Таким образом, математической моделью решаемой задачи является составленное дифференциальное уравнение 1-го порядка относительно функции

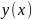
Требуется найти общее решение этого ДУ.

Решим составленную математическую модель

упростим ДУ с целью привести его к канонической форме

ДУ I порядка :

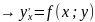В результате получили однородное ДУ;

Решаем его заменой , в результате

которой однородное ДУ приводится к ДУ с разделяющимися переменными

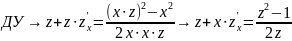
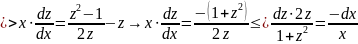
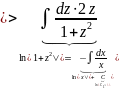
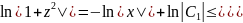
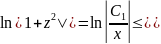
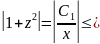
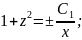
Переобозначим и сделаем обратную замену :

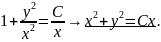
Получим для составленного ДУ общее решение в неявном виде, оно называется общим интегралом ДУ

Интерпретация решения ДУ, проверка его достоверности

Общий интеграл ДУ задает семейство интегральных линий, которые имеют уравнение

.

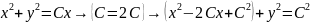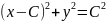- это семейство окружностей с центром в точке (C;0) и радиусом |C|, где C – произвольно изменяющаяся величина, постоянная относительно переменных x и y.

Замечаем, что при C=0 окружность превращается в точку 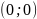, следовательно, поставленная задача не имеет решения.

Если проанализировать теорему существования и единственности частных решений для ДУ 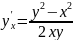, то хорошо видны его особые точки – это такие точки, в которых 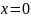или . Следовательно, составленная математическая модель задачи не дает решение для точек с или .

Ответ по задаче:

Условию задачи удовлетворяют окружности 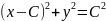, в которых .

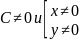Задание 5

Моторная лодка движется в спокойной воде со скоростью 10 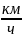. На полном ходу её мотор был выключен и за 20 секунд лодки уменьшилась до 6 . Считая, что сила сопротивления воды пропорциональна скорости лодки, найти:

1. скорость лодки через 2 минуты;

2. расстояние, пройденное лодкой за 1 минуту после остановки мотора.

Решение

Произведем разбор условия задачи

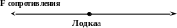
Дано:

t=0 – момент времени, когда выключен мотор. (начальный момент промежутка времени, в течении которого далее наблюдается физический процесс)

;

;

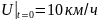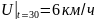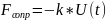, где k – коэффициент пропорциональности.

Найти:

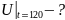
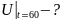
Составим математическую модель к данной задаче

Искомые величины в задаче

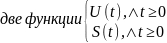
Связь между этими функциями:

Значит для составления уравнения используем II-й закон Ньютона:

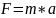, где m – масса тела;

a – ускорение;

F(t) – равнодействующая всех сил, действующих на тело

По физическому смыслу производных имеем, что

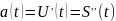
По условию задачи

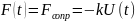
Тогда уравнение относительно функции U(t):

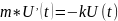– Составлено ДУ I-го порядка, в котором m и k – константы по t.

Решим составленную математическую модель

Общее уравнение:

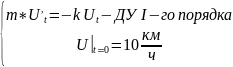
т.к. ДУ относится к типу с разделенными переменными:

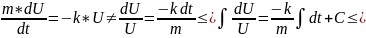
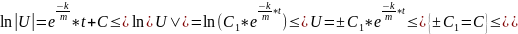
- общее решение ДУ;

Начальное условие:

.

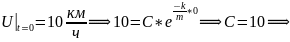
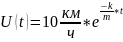Интерпретация решения математической модели и получение ответов на вопросы задачи

.

.

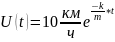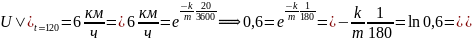
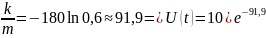Скорость через 2 минуты = часа.

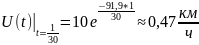
Находим закон изменения расстояния S(t), пройденного лодкой после остановки мотора.

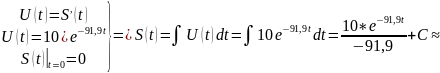
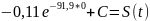
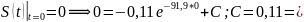
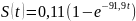
Вычислим расстояние, пройденное лодкой за 1 минуту:

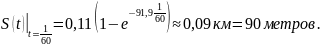
Ответ по задаче:

1. Скорость лодки через 2 минуты ;

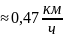2. Расстояние, пройденное лодкой через 1 минуту после остановки, = 90 метров.