2.1.2.4 Значения накопленных опытных вероятностей (частостей)

Значения накопленных вероятностей (последняя строка ряда) определяют суммированием вероятностей по интервалам.

(5)

Для нашего примера:

;

и т.д. по другим интервалам.

2.1.3 Определение числовых характеристик

Основными числовыми характеристиками распределения случайной величины являются среднее значение, среднее квадратическое отклонение и коэффициент вариации.

Среднее квадратическое отклонение представляет собой абсолютную меру, а коэффициент вариации – относительную меру рассеивания (разброса) случайной величины. При объеме выборки (информации) N25 их определяют следующим образом.

Среднее значение ресурса определяется по формуле:

, мото-ч., (6)

где Т_срi – значение ресурса в середине i-го интервала;

Р_i – опытная вероятность в i-ом интервале.

Для нашего примера:

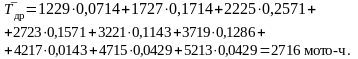
Среднее квадратическое отклонение определяется по формуле:

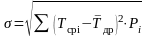, мото-ч. (7)

Для нашего примера:

= 1009 мото-ч.

Коэффициент вариации определяется по формуле:

(8)

Для нашего примера:

2.1.4 Проверка информации на наличие выпадающих точек

Проверку информации на наличие выпадающих точек осуществляют по формуле:

, (9)

где T_i и T_i-1 – смежные точки в сводной ведомости информации (см. таблицу 1).

В нашем примере:

для наименьшего значения ресурса

Т₁=980 мото-ч.; Т₂=1272 мото-ч.; ;

для наибольшего значения ресурса

Т₇₀=5460 мото-ч.; Т₆₉=5220 мото-ч.; ;

Полученные значения сравнивают с табличными значениями критерия Ирвина (Приложение Б, таблица Б1).

Если λ_оп < λ_т то информация достоверна, если же λ_оп > λ_т, то такие точки «выпадают», т.е. должны быть исключены из информации как недостоверные. В этом случае необходимо перестроить статистический ряд с учетом уменьшения количества информации за счет выпавших точек и вновь рассчитать 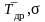и V.

В нашем случае при N=70 и доверительной вероятности =0,95 табличное значение критерия Ирвина _Т = 1,1, т.е. больше _оп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.

2.1.5 Построение гистограммы, полигона и кривой накопленных опытных вероятностей

Данные таблицы 2 используют для построения графиков, наглядно характеризующих опытное распределение случайной величины (в данном случае ресурса гильзы): гистограммы 1, полигона 2 и кривой накопленных опытных вероятностей 3 (рисунок 1). При построении опытного распределения ресурсов на оси абсцисс откладывается в произвольно выбранном масштабе значение ресурса, а по оси ординат – опытная вероятность Р_i и накопленная опытная вероятность _i.

Масштаб ординаты следует выбирать, придерживаясь правила «золотого сечения»:

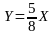, (10)

где Y – длина наибольшей ординаты;

Х – длина абсциссы, соответствующая наибольшему значению ресурса.

Построение гистограммы осуществляется следующим образом (см. рисунок 1). По оси абсцисс откладывают интервалы в соответствии со статистическим рядом, а по оси ординат опытную вероятность Р_i в начале и в конце каждого интервала. Соединив построенные в каждом интервале точки, получают прямоугольник. В результате образуется ступенчатый многоугольник-гистограмма. Площадь каждого многоугольника в процентах от общей площади гистограммы или долях единицы определяет опытную вероятность или количество деталей, у которых ресурс находится в данном интервале.

Построение полигона (см. рисунок 1) осуществляется по точкам, образованным пересечением абсциссы, равной середине интервала, и ординаты, равной опытной вероятности интервала, т.е. надо соединить прямыми линиями середины верхних (горизонтальных) сторон прямоугольников гистограммы. Начальная и конечная точки поли-

Рисунок 1 – Гистограмма (1), полигон (2) и кривая накопленных опытных вероятностей (3) распределения ресурсов гильз цилиндров

гона на оси абсцисс должны быть смещены на пол-интервала относительно начала первого и конца последнего интервалов соответственно влево и вправо.

Точки кривой накопленных опытных вероятностей образуются пересечением абсциссы, равной концу данного интервала, и ординаты, равной сумме вероятностей предыдущих интервалов (см. рисунок 1). Гистограмма и полигон являются дифференциальными, а кривая накопленных опытных вероятностей – интегральным статистическим (опытным) законом распределения случайной величины.