27

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Глазовский государственный педагогический

институт им. В.Г. Короленко

Кафедра алгебры, геометрии, теории и методики

обучения математике

Тексты лекций по алгебре

(для студентов первого курса математического факультета)

Глазов 2007

Методическая разработка по алгебре предназначена для студентов первого курса математического факультета по специальности 032100.01 – «Математика» с дополнительной специальностью «Информатика».

Составитель: канд. физ.-мат. наук, доцент Г.Г. Щепин

Алгебраические операции. Алгебры. Введение в числовые системы Алгебраические операции

Будем рассматривать только непустые множества и считать известными понятия декартового произведения, отношения, заданного на одном или нескольких множествах. Воспользуемся стандартными сокращениями:

1. определение – О;

2. доказательство – Д.

В процессе развития науки, включая и математику, содержание предмета алгебры менялось. Примерно до середины 19 века в исследованиях по алгебре значительное место занимали вопросы, связанные с решением уравнений, неравенств и их систем, совершенствованием методов их приближенных решений. К указанным вопросам тесно примыкают теория матриц, определителей и некоторые другие теории.

Начиная с середины 19 века, точнее со второй его половины, алгебра, являющаяся, по выражению академика А.И. Мальцева (1909-1967), наиболее подвижной частью математики, получает мощный толчок в своем развитии. Существенно меняется характер ее исследований.

Основным предметом изучения алгебры становятся множества с заданными на них алгебраическими операциями, так называемые универсальные алгебры. В настоящее время предмет алгебры уже принято понимать в более широком смысле, а именно, - изучение множеств с определенными на них алгебраическими операциями и отношениями, называемых алгебраическими системами.

О. Говорят, что на множестве М задана бинарная алгебраическая операция или просто бинарная операция , если указано правило, сопоставляющее произвольной паре элементов а и в из М, взятым в определенном порядке, однозначно определенный элемент с из этого же множества М и обозначается .

Возможны и другие обозначения операции, например, или Т, т.е. ( ).

Формально эту операцию можно рассматривать как отображение декартова произведения М М в М.

Различают нульместную (нулярную) и унарную операции.

О. Нульместной операцией на множестве М называют выделение (фиксирование) какого-нибудь элемента из М, причем каждая нульместная операция фиксирует лишь один элемент из М. Число 0 называют рангом нульместной операции.

О. Унарная операция на М – это отображение М в М или обычная одноместная функция, область определения которой совпадает с М. Унарной операции приписывают ранг 1 и называют также оператором.

Понятие алгебраической операции может быть определено для любого ранга n.

О. Пусть Мⁿ есть n-ая степень непустого множества М. Отображение множества Мⁿ в М называют n-местной алгебраической операцией или просто n-местной операцией на множестве М.

При n=3 операцию называют тернарной, но чаще всего рассматривают бинарные операции.

Если не для любого элемента из Мⁿ существует образ в М, то операцию называют частичной. Например, вычитание во множестве натуральных чисел N является частичной операцией.

Бинарные операции могут обладать рядом свойств:

коммутативностью, ассоциативностью, сократимостью слева (справа) и просто сократимостью, дистрибутивностью одной операции относительно другой, существованием левого и правого нейтральных элементов, обозначаемых соответственно и , а также просто нейтрального элемента е. Кроме того, если бинарная операция обладает нейтральным элементом еМ, то для любого элемента аМ могут существовать правый и левый симметричные к нему элементы, обозначаемыми соответственно а^{^} и ^{^}а, и просто симметричный к нему (могут быть и другие обозначения). Определения указанных свойств можно найти в [1] и [3].

Операции могут обладать и некоторыми другими свойствами. Отметим некоторые из них.

О. Элемент называется поглощающим слева (справа) относительно операции , если для любого элемента хМ имеет место равенство ( ), и поглощающим (аннулятором), если он поглощающий слева и справа.

О. Операция  называется идемпотентной, если для любого хМ .

Упр. 1. Пусть М – непустое множество, Р(М) – множество всех его подмножеств, называемый его булеаном. Докажите, что операция нахождения разности на Р(М) не является ассоциативной.

Упр. 2. Докажите, что декартово умножение множеств дистрибутивно относительно разности.

Упр. 3. Докажите, что если для операции  существуют и , то они совпадают, и для этой операции нет других нейтральных элементов.

Упр. 4. Докажите, что если для операции  на множестве М существуют для элемента аМ симметричные элементы а^{^} и ^{^}а, то они совпадают, и симметричный элемент для а единственный.

Упр. 5. Пусть задана операция  на множестве N такая, что . Найдите поглощающий элемент. Является ли эта операция идемпотентной?

Аддитивная и мультипликативная формы записи операций. Чаще всего используются аддитивная и мультипликативная формы записи бинарной операции, называемые соответственно сложением и умножением и обозначаемыми знаками + и (иногда вместо используется и так называемый «немой» знак). Но наиболее распространенной является мультипликативная запись.

В связи с этим изменяется и терминология понятий заданной операции, которую можно записать в виде следующей таблицы:

Операция общего вида	умножение или «немой» знак	сложение +
Результат операции	произведение	сумма
Нейтральный элемент	единичный элемент е и т.п.)	нулевой элемент 0 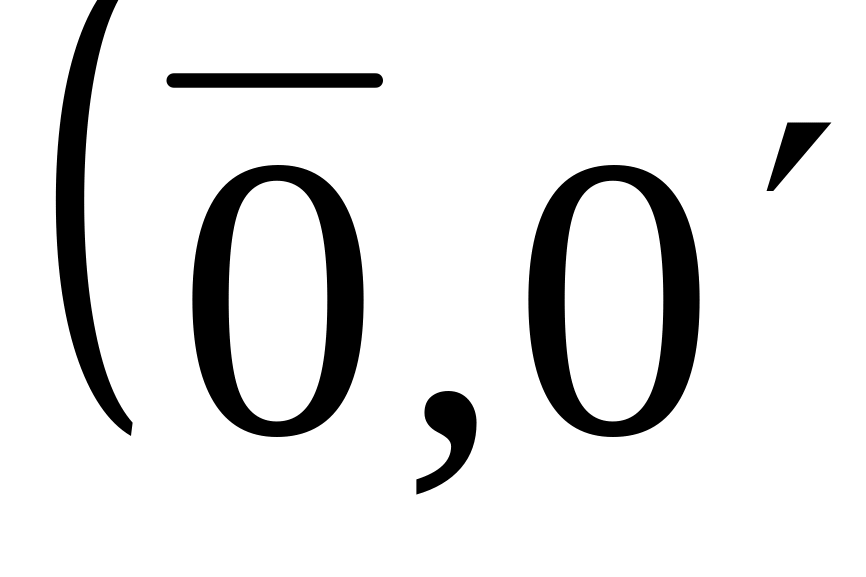и т.п.)
Симметричный элемент для а ( )	обратный для а	противоположный для а (-а)