15. Абсолютная непрерывность меры относительно другой меры. Абсолютные непрерывные функции и порожденные ими меры Лебега-Стилтьеса.Функция Кантора.

Построим подмн-во следующим образом. Разделим отрезок [0,1] на три равные части и выбросим средний интервал . Получим множество , состоящее из двух отрезков мера которого равна 2/3. Каждый из отрезков и мн-ва делим на три равные части и из каждого выбрасываем средний интервал, т.е. множество . Получаем множество мера которого . Далее для построения мн-ва каждый из отрезков, составляющих мн-во , делим на три равные части и средний интервал, имеющий длину , выбрасываем. Выброшенное множество обозначим как . Полагаем , при этом имеем .

Мн-во называется множеством Кантора. Это замкнутое множество, так как замкнуты. А пересечение замкнутых мн-в замкнуто. В силу непрерывности меры имеем .

Мн-во K имеет мощность континуума. Это можно показать следующим образом. Каждое число можно представить в виде троичной дроби

Где числа могут принимать значения 0,1,2. С помощью такого представления легко описать те числа, которые попадают в канторово мн-во. Заметим , что число 1/3 принадлежащее К, в разложении которого = 1, , можно записать другим способом: без использования цифры 1. Таким образом, числа, принадлежащие К могут быть записаны в виде троичной дроби так, чтобы в числителях не встречалось число 1. В результате установлено взаимно однозначное соответствие между точками из К и всеми последовательностями из 0 и 2, которые находятся во взаимно однозначном соответствии с последовательностями из 0 и 1. А всякую последовательность из 0 и 1 можно рассматривать как двоичную запись некоторого действительного числа из [0,1]. Получаем отображение из К на [0,1]. Отсюда К имеет мощность континуума

Опр.Мера µ: S→R назыв. счетно-аддитивной (σ- аддитивной), если из того, что A= , A,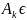 S, следует, что (A)= .

Теор. Длина явл. 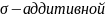мерой на полукольце S, состоящем из полуинтервалов вида

Опр. Мера на кольце K назыв. непрерывной, если для монотонно возрастающей (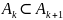 )последовательности множеств такой, что A:= , справедливо равенство .

Теор. Мера на кольце K явл. σ- аддитивной iff она непрерывна.

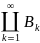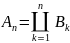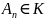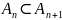Пусть мера σ- аддитивна и , где такие, что . Тогда A= ... и . Обратно пусть мера непрерывна и пусть A= , . Положим . Тогда , , A= и в силу свойства непрерывности .

Зам. С помощью перехода к дополнению легко проверить, что свойство непрерывности меры эквивалентно следующему : для множеств таких, что 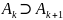и A= , выполнено .

Опр. Мера , заданная на полукольце K, наз.продолжением меры m, заданной на полукольце S, если:

1. S K,

2. 

Опр: Числовая функция F(t) называется непрерывной слева в точке t₀, если для любого >0 существует δ>0 такое,что из t₀-δ≤t≤ t₀ следует неравенство |F(t) – F(t₀)|< , или, что эквивалентно, для любой последовательности t_n-> t₀, такой, что t_n≤ t₀, выполнено F(t_n)->F(t₀)

15. Абсолютная непрерывность меры относительно другой меры. Абсолютные непрерывные функции и порожденные ими меры Лебега-Стилтьеса.Функция Кантора.

Th: Для того,чтобы мера m была σ-аддитивной,необходимо и достаточно, чтобы производящая функция F(t) была непрерывна слева в каждой точке. Proof: Необходимость. Пусть m - σ-аддитивная мера. Возьмем последовательность b_n-> b, b_n<b_n+1<b. Пусть A_n = [a,b_n[. Тогда A₁cA₂c… и [a,b[ = _n. По теорему о непрерывности меры имеем F(b) – F(a) =m([a,b[) = _n[)= (b_n)-F(a). Таким образом, F(b) = (b_n) для любой монотонно возрастающей последовательности b_n->b. Отсюда следует непрерывность функции F слева. Достаточность. Пусть А=[a,b[, A_k=[a_k,b_k[, A= _k. Требуется доказать, что F(b)-F(a)= _k)-F(a_k)). Так как, согласно теореме о продолжении меры, _k) ≤ F(b)-F(a), то достаточно доказать обратное неравенство. Возьмем >0 и по каждому из полуинтегралов [a_k,b_k[, построим содержащий его открытый интервал B_k=(a_k’,b_k’[, где a_k’ выбрано так, чтобы F(a_k)-F(a_k’)< 2^k+1. Это можно сделать в силу непрерывности слева функции F в точке a_k. Вместо полуинтервала [a,b[ возьмем содержащий в нем отрезок B=[a,b’] такой, что F(b)-F(b’)< Тогда B c A c _k c _k, т.е. отрезок B покрыт системой открытых интервалов B_k.

Согласно лемме Бореля, из этого покрытия можно выделить конечное подпокрытие, т.е существует такое n, что B c _k. Так как приращение монотонной функции на отрезке не превосходит суммы приращений на соответствующих интервалах, имеем F(b’)-F(a) ≤ F(b_k)-F(a_k’))≤ F(b_k)-F(a_k)+ ^k+1] ≤ F(b_k) –F(a_k)]+ Далее получаем F(b)-F(a)≤ F(b’)-F(a)+ ≤ F(b_k) –F(a_k)]+ Ввиду произведения , переходя к пределу при имеем F(b)-F(a) = F(b_k)-F(a_k)]

Лебеговское продолжение меры,порожденной непрерывной слева фугкцией F, называется мерой Лебега-Стильтьеса и обычно обозначается µ_F